矩阵的逆：

矩阵的逆有是三种方法可以求

1、系数待定法： 

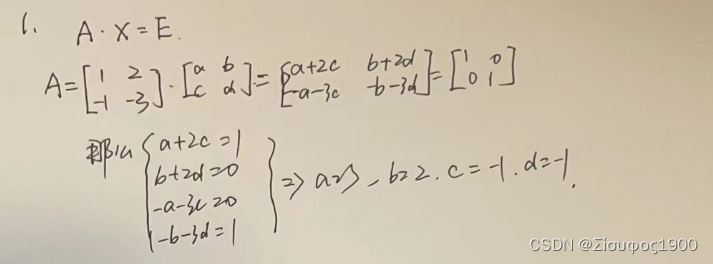
2、求伴随矩阵求逆

 

 3、通过求增广矩阵求出逆 

矩阵的迹

什么是矩阵的迹

矩阵的迹是特征值的加和，也即矩阵A的主对角线元素的总和。

案例

矩阵的秩

什么是矩阵的秩

设 AA 为 m\times nm×n 矩阵。若 AA 至少有一个 rr 阶非零子式，而其所有 {\displaystyle r+1}r+1阶子式全为零，则称 rr 为AA 的秩

在线性代数中，一个矩阵Ａ的列秩是Ａ的线性无关的纵列的极大数。类似的，行秩是Ａ的线性无关的橫行的极大数目。

直观理解矩阵的秩：

• 秩是图像经过矩阵变换后的空间维度
• 列空间的维度

矩阵秩的性质：

A是在域F上的m × n矩阵并描述了上述线性映射。

• 只有零矩阵有秩0
• A的秩最大为min(m,n)
• f是单射，当且仅当A有秩n（在这种情况下，我们称A有“列满秩”）。
• f是满射，当且仅当A有秩m（在这种情况下，我们称A有“行满秩”）。
• 在方块矩阵A (就是m = n)的情况下，则A是可逆的，当且仅当A有秩n（也就是A有满秩）。线

线性关系：

将m个n维列向量排列成n×m的矩阵A，这个对应矩阵的秩即为原向量组的秩

原向量组线性相关的充分必要条件为：r(A)<m
如果r(A) = m 则向量组线性无关。

r(A)≤n<m
这个向量组必然线性相关。

计算矩阵的秩：

 那么通过高斯消元法：

 r(A)=2