总览
在这里,我们放宽了流行的线性方法的假设。最近我们被客户要求撰写关于非线性模型的研究报告,包括一些图形和统计输出。有时线性假设只是一个很差的近似值。有许多方法可以解决此问题,其中一些方法可以通过使用正则化方法降低模型复杂性来 解决 。但是,这些技术仍然使用线性模型,到目前为止只能进行改进。本文本专注于线性模型的扩展
相关视频:非线性模型原理与R语言多项式回归、局部平滑样条、 广义相加模型GAM分析
非线性模型原理与R语言多项式回归、局部平滑样条、 广义相加模型GAM分析
,时长05:41
视频:R语言广义相加模型(GAM)在电力负荷预测中的应用
拓端tecdat:R语言广义相加模型(GAM)在电力负荷预测中的应用
-
多项式回归 这是对数据提供非线性拟合的简单方法。
-
阶跃函数 将变量的范围划分为 K个 不同的区域,以生成定性变量。这具有拟合分段常数函数的效果。
-
回归样条 比多项式和阶跃函数更灵活,并且实际上是两者的扩展。
-
局部样条曲线 类似于回归样条曲线,但是允许区域重叠,并且可以平滑地重叠。
-
平滑样条曲线 也类似于回归样条曲线,但是它们最小化平滑度惩罚的残差平方和准则 。
-
广义加性模型 允许扩展上述方法以处理多个预测变量。
多项式回归
这是扩展线性模型的最传统方法。随着我们增加 多项式的项,多项式回归使我们能够生成非线性的曲线,同时仍使用最小二乘法估计系数。
逐步回归
它经常用于生物统计学和流行病学中。
回归样条
回归样条是 扩展多项式和逐步回归技术的许多基本函数之一 。事实上。多项式和逐步回归函数只是基 函数的特定情况 。
这是分段三次拟合的示例(左上图)。
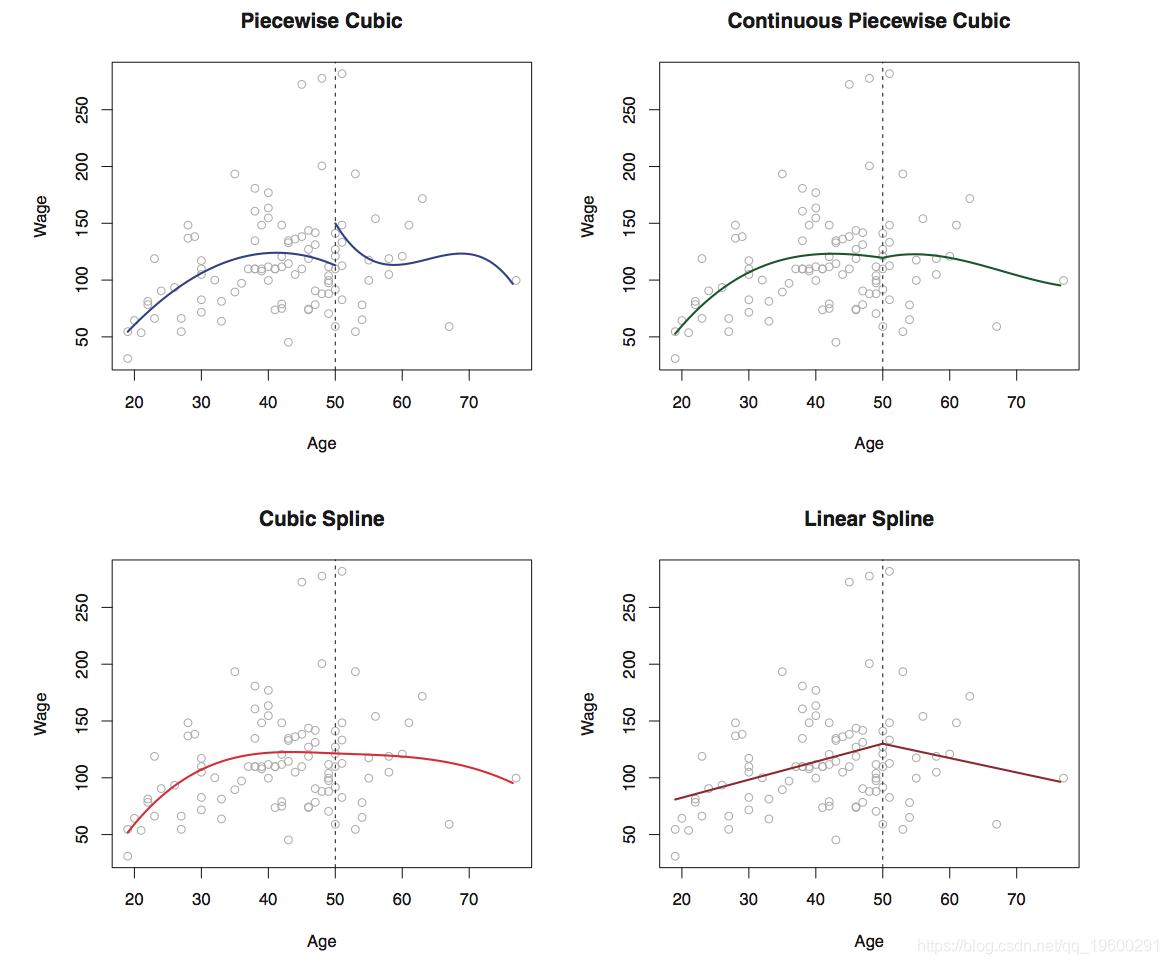
为了解决此问题,更好的解决方案是采用约束,使拟合曲线必须连续。
选择结的位置和数量
一种选择是在我们认为变化最快的地方放置更多的结,而在更稳定的地方放置更少的结。但是在实践中,通常以统一的方式放置结。
要清楚的是,在这种情况下,实际上有5个结,包括边界结。
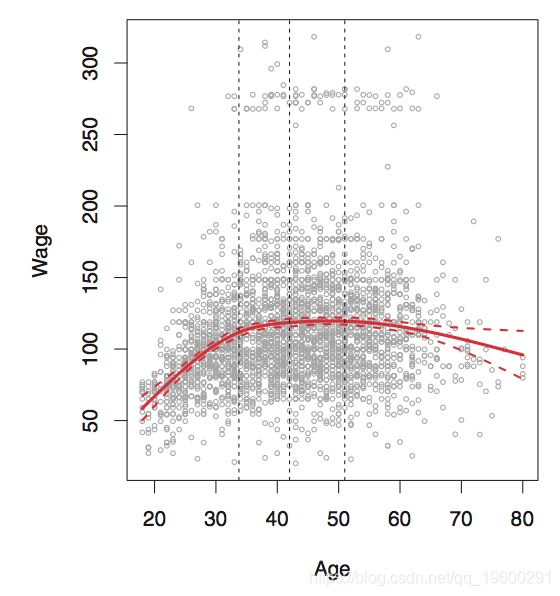
那么我们应该使用多少个结?一个简单的选择是尝试许多个结,然后看哪个会产生最好的曲线。但是,更客观的方法是使用交叉验证。
与多项式回归相比,样条曲线可以显示出更稳定的效果。
平滑样条线
我们讨论了回归样条曲线,该样条曲线是通过指定一组结,生成一系列基函数,然后使用最小二乘法估计样条系数而创建的。平滑样条曲线是创建样条曲线的另一种方法。让我们回想一下,我们的目标是找到一些非常适合观察到的数据的函数,即最大限度地减少RSS。但是,如果对我们的函数没有任何限制,我们可以通过选择精确内插所有数据的函数来使RSS设为零。
选择平滑参数Lambda
同样,我们求助于交叉验证。事实证明,我们实际上可以非常有效地计算LOOCV,以平滑样条曲线,回归样条曲线和其他任意基函数。
平滑样条线通常比回归样条线更可取,因为它们通常会创建更简单的模型并具有可比的拟合度。
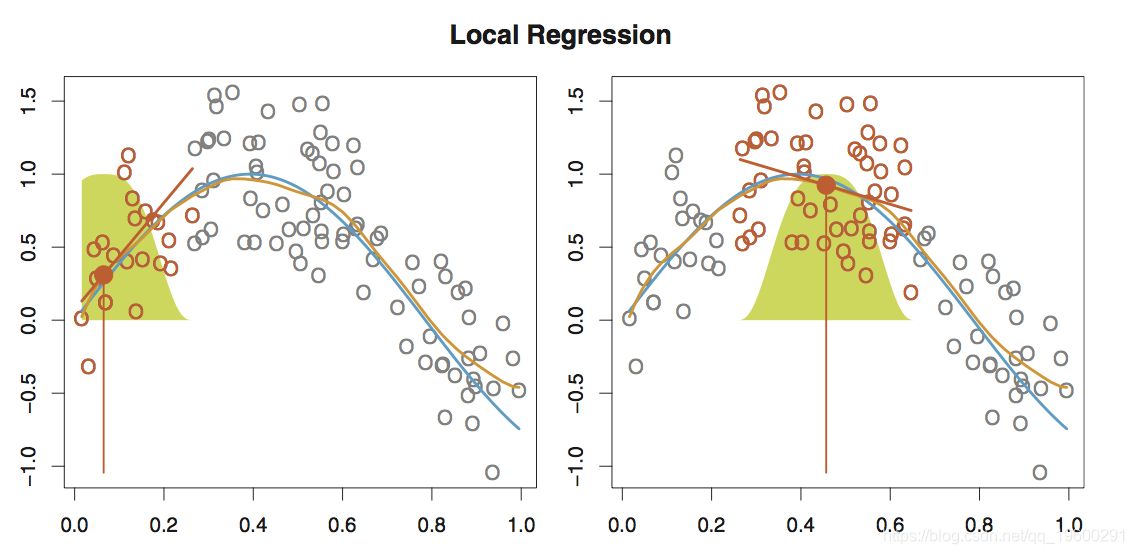
局部回归
局部回归涉及仅使用附近的训练观测值来计算目标点x 0 处的拟合度 。
可以通过各种方式执行局部回归,尤其是在涉及拟合p 线性回归模型的多变量方案中尤为明显 ,因此某些变量可以全局拟合,而某些局部拟合。
广义加性模型
GAM模型提供了一个通用框架,可通过允许每个变量的非线性函数扩展线性模型,同时保持可加性。
具有平滑样条的GAM并不是那么简单,因为不能使用最小二乘。取而代之的 是使用一种称为反向拟合的方法 。
GAM的优缺点
优点
-
GAM允许将非线性函数拟合到每个预测变量,以便我们可以自动对标准线性回归会遗漏的非线性关系进行建模。我们不需要对每个变量分别尝试许多不同的转换。
-
非线性拟合可以潜在地对因变量Y做出更准确的预测 。
-
因为模型是可加的,所以我们仍然可以检查每个预测变量对Y的影响, 同时保持其他变量不变。
缺点
- 主要局限性在于该模型仅限于累加模型,因此可能会错过重要的交互作用。
范例
多项式回归和阶跃函数
library(ISLR)
attach(Wage)我们可以轻松地使用来拟合多项式函数,然后指定多项式的变量和次数。该函数返回正交多项式的矩阵,这意味着每列是变量的变量的线性组合 age, age^2, age^3,和 age^4。如果要直接获取变量,可以指定 raw=TRUE,但这不会影响预测结果。它可用于检查所需的系数估计。
fit = lm(wage~poly(age, 4), data=Wage)
kable(coef(summary(fit)))
现在让我们创建一个ages 我们要预测的向量。最后,我们将要绘制数据和拟合的4次多项式。
ageLims <- range(age)
age.grid <- seq(from=ageLims[1], to=ageLims[2])
pred <- predict(fit, newdata = list(age = age.grid),
se=TRUE)
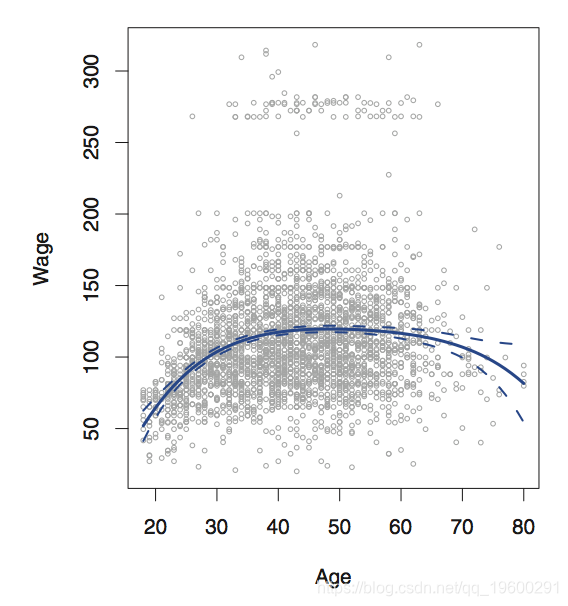
plot(age,wage,xlim=ageLims ,cex=.5,col="darkgrey")
lines(age.grid,pred$fit,lwd=2,col="blue")
matlines(age.grid,se.bands,lwd=2,col="blue",lty=3) 在这个简单的示例中,我们可以使用ANOVA检验 。
在这个简单的示例中,我们可以使用ANOVA检验 。
## Analysis of Variance Table
##
## Model 1: wage ~ age
## Model 2: wage ~ poly(age, 2)
## Model 3: wage ~ poly(age, 3)
## Model 4: wage ~ poly(age, 4)
## Model 5: wage ~ poly(age, 5)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 2998 5022216
## 2 2997 4793430 1 228786 143.59 <2e-16 ***
## 3 2996 4777674 1 15756 9.89 0.0017 **
## 4 2995 4771604 1 6070 3.81 0.0510 .
## 5 2994 4770322 1 1283 0.80 0.3697
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
我们看到,_M_1 与二次模型 相比,p值 _M_2 实质上为零,这表明线性拟合是不够的。 因此,我们可以得出结论,二次方或三次模型可能更适合于此数据,并且偏向于简单模型。
我们也可以使用交叉验证来选择多项式次数。

在这里,我们实际上看到的最小交叉验证误差是针对4次多项式的,但是选择3次或2次模型并不会造成太大损失。接下来,我们考虑预测个人是否每年收入超过25万。
但是,概率的置信区间是不合理的,因为我们最终得到了一些负概率。为了生成置信区间,更有意义的是转换对 数 预测。
绘制:
plot(age,I(wage>250),xlim=ageLims ,type="n",ylim=c(0,.2))
lines(age.grid,pfit,lwd=2, col="blue")
matlines(age.grid,se.bands,lwd=1,col="blue",lty=3)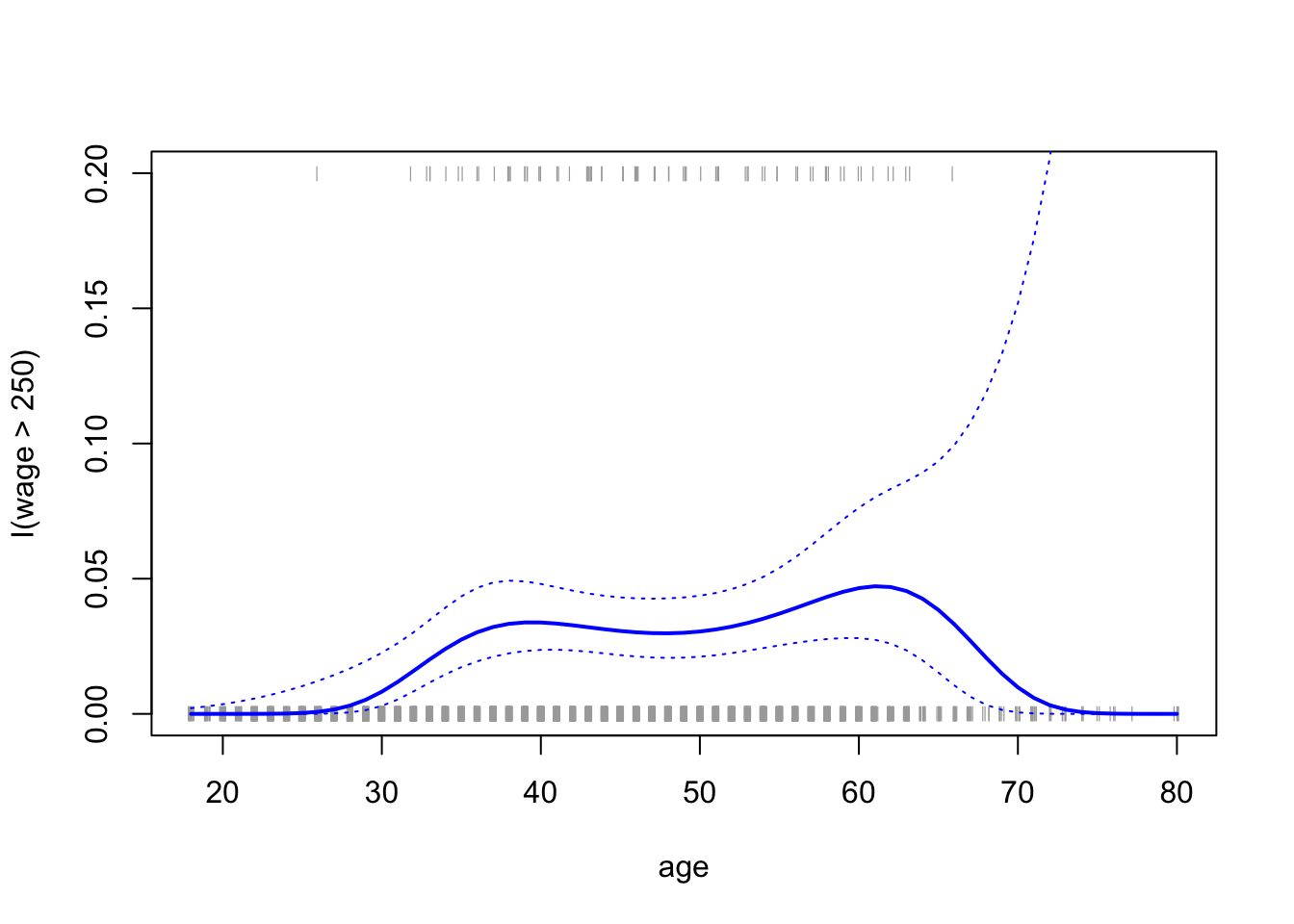
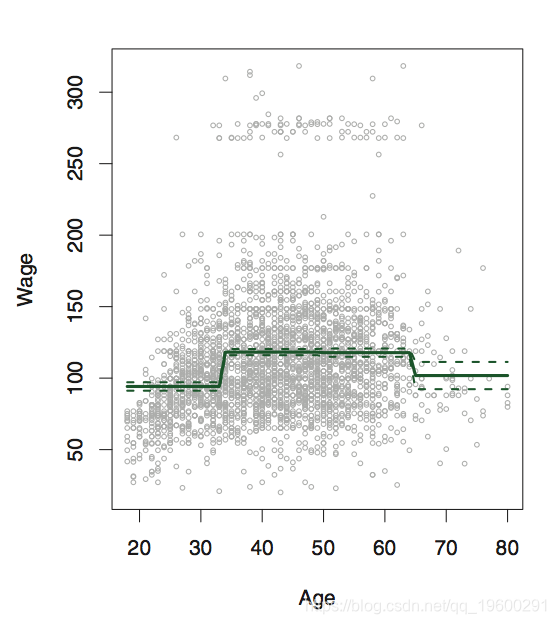
逐步回归函数
在这里,我们需要拆分数据。
table(cut(age, 4))
##
## (17.9,33.5] (33.5,49] (49,64.5] (64.5,80.1]
## 750 1399 779 72fit <- lm(wage~cut(age, 4), data=Wage)
coef(summary(fit))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 94.158 1.476 63.790 0.000e+00
## cut(age, 4)(33.5,49] 24.053 1.829 13.148 1.982e-38
## cut(age, 4)(49,64.5] 23.665 2.068 11.443 1.041e-29
## cut(age, 4)(64.5,80.1] 7.641 4.987 1.532 1.256e-01splines 样条函数
在这里,我们将使用三次样条。

由于我们使用的是三个结的三次样条,因此生成的样条具有六个基函数。
## [1] 3000 6
dim(bs(age, df=6))
## [1] 3000 6
## 25% 50% 75%
## 33.75 42.00 51.00
拟合样条曲线。
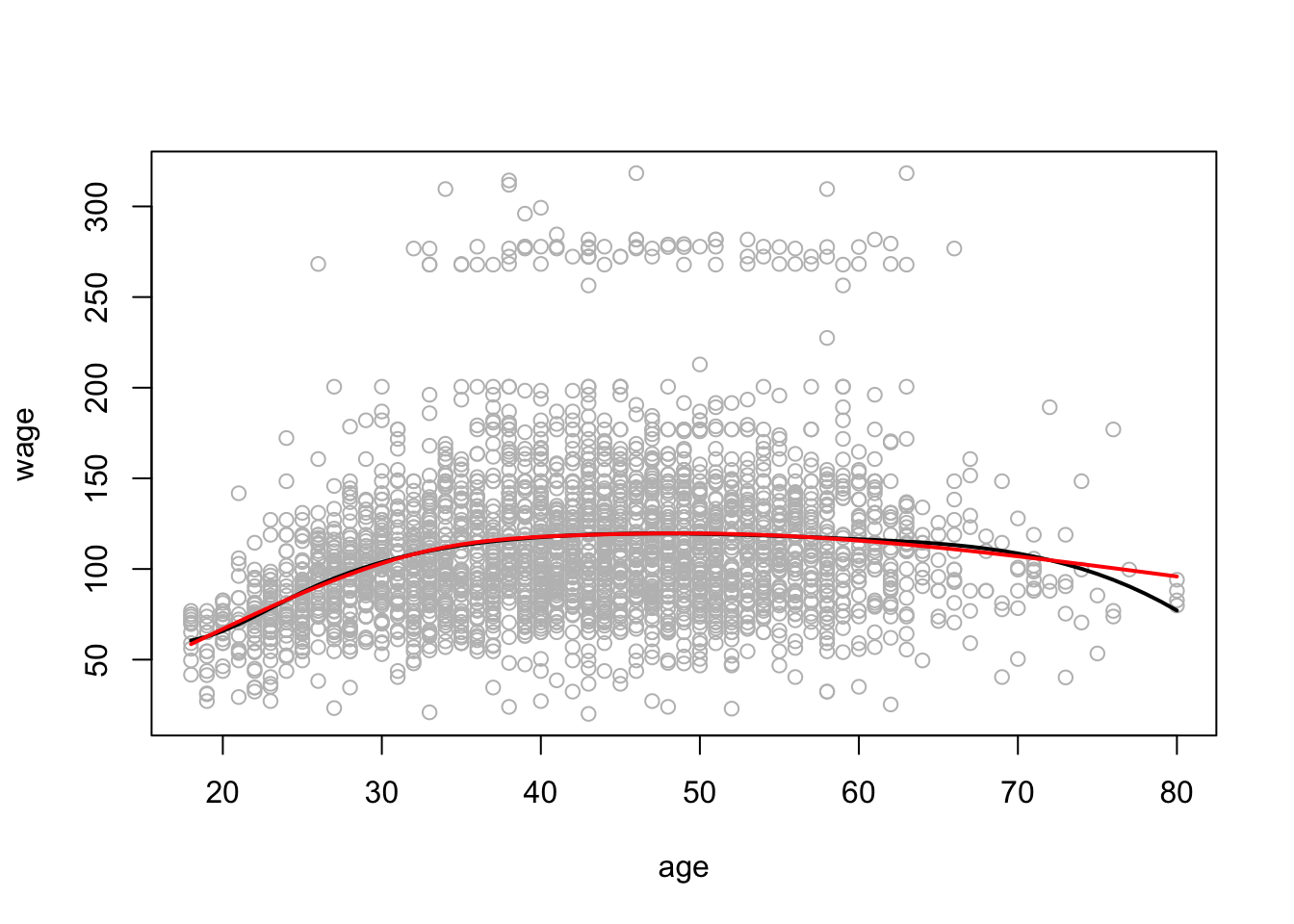
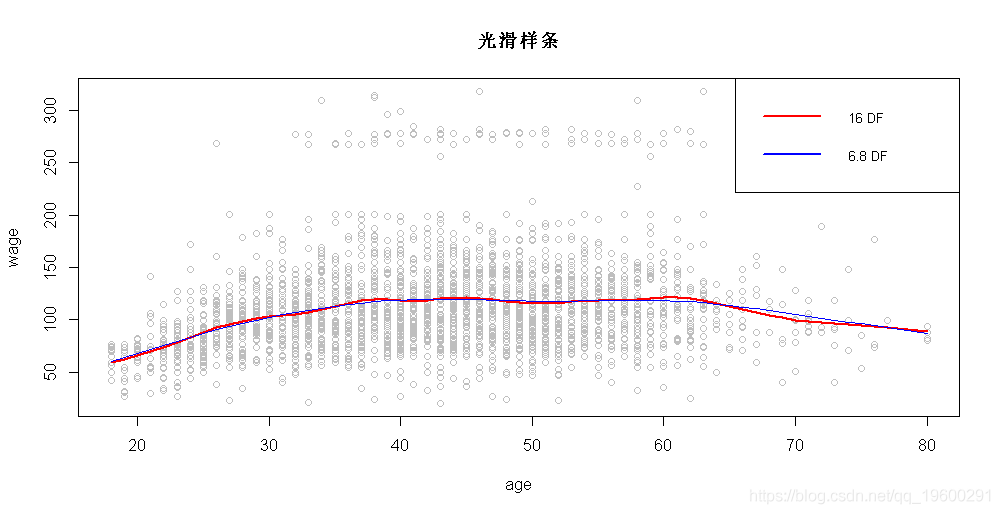
我们也可以拟合平滑样条。在这里,我们拟合具有16个自由度的样条曲线,然后通过交叉验证选择样条曲线,从而产生6.8个自由度。
fit2$df
## [1] 6.795
lines(fit, col='red', lwd=2)
lines(fit2, col='blue', lwd=1)
legend('topright', legend=c('16 DF', '6.8 DF'),
col=c('red','blue'), lty=1, lwd=2, cex=0.8)
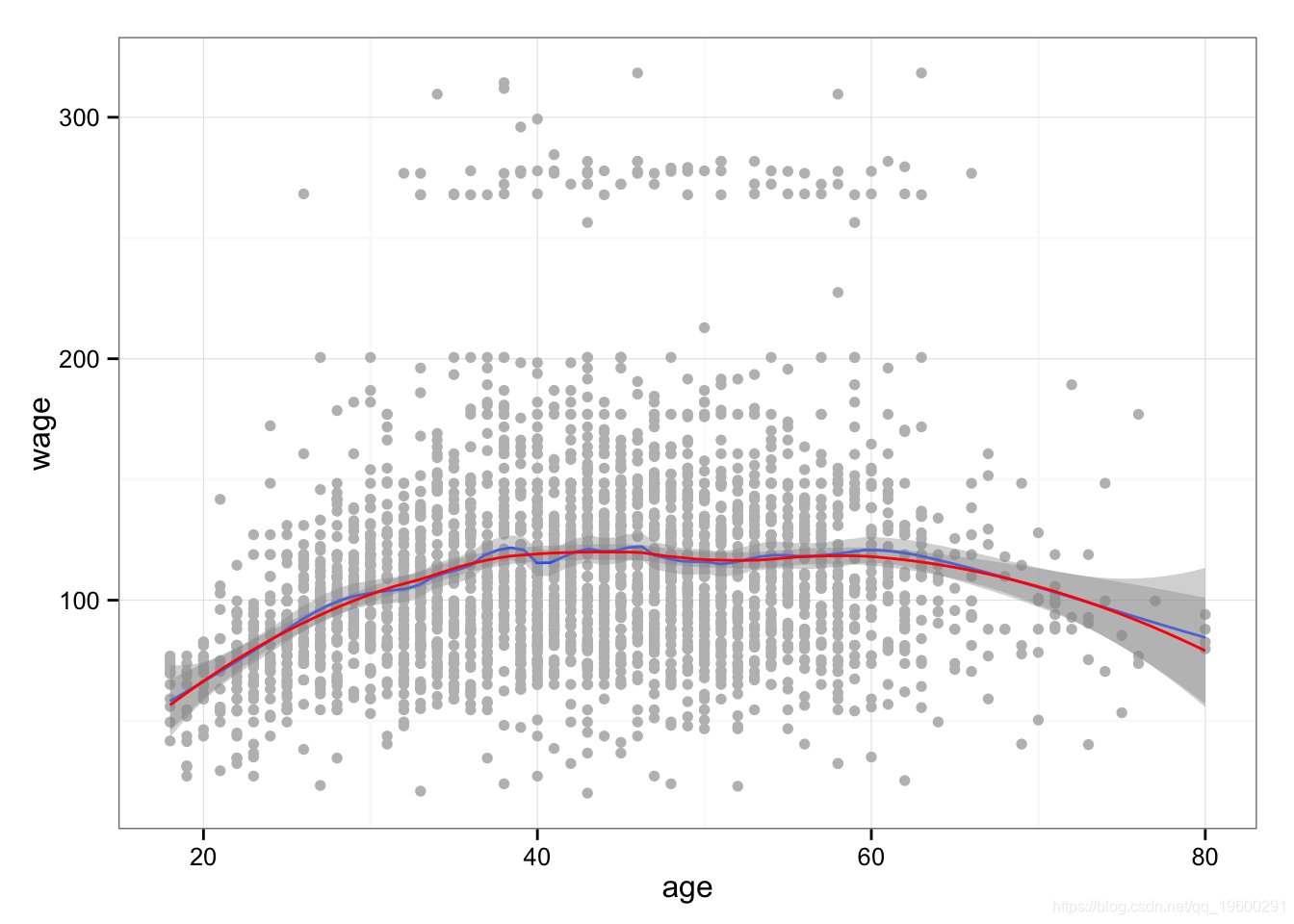
局部回归
执行局部回归。
GAMs
现在,我们使用GAM通过年份,年龄和受教育程度的样条来预测工资。由于这只是具有多个基本函数的线性回归模型,因此我们仅使用 lm() 函数。
为了拟合更复杂的样条曲线 ,我们需要使用平滑样条曲线。
绘制这两个模型
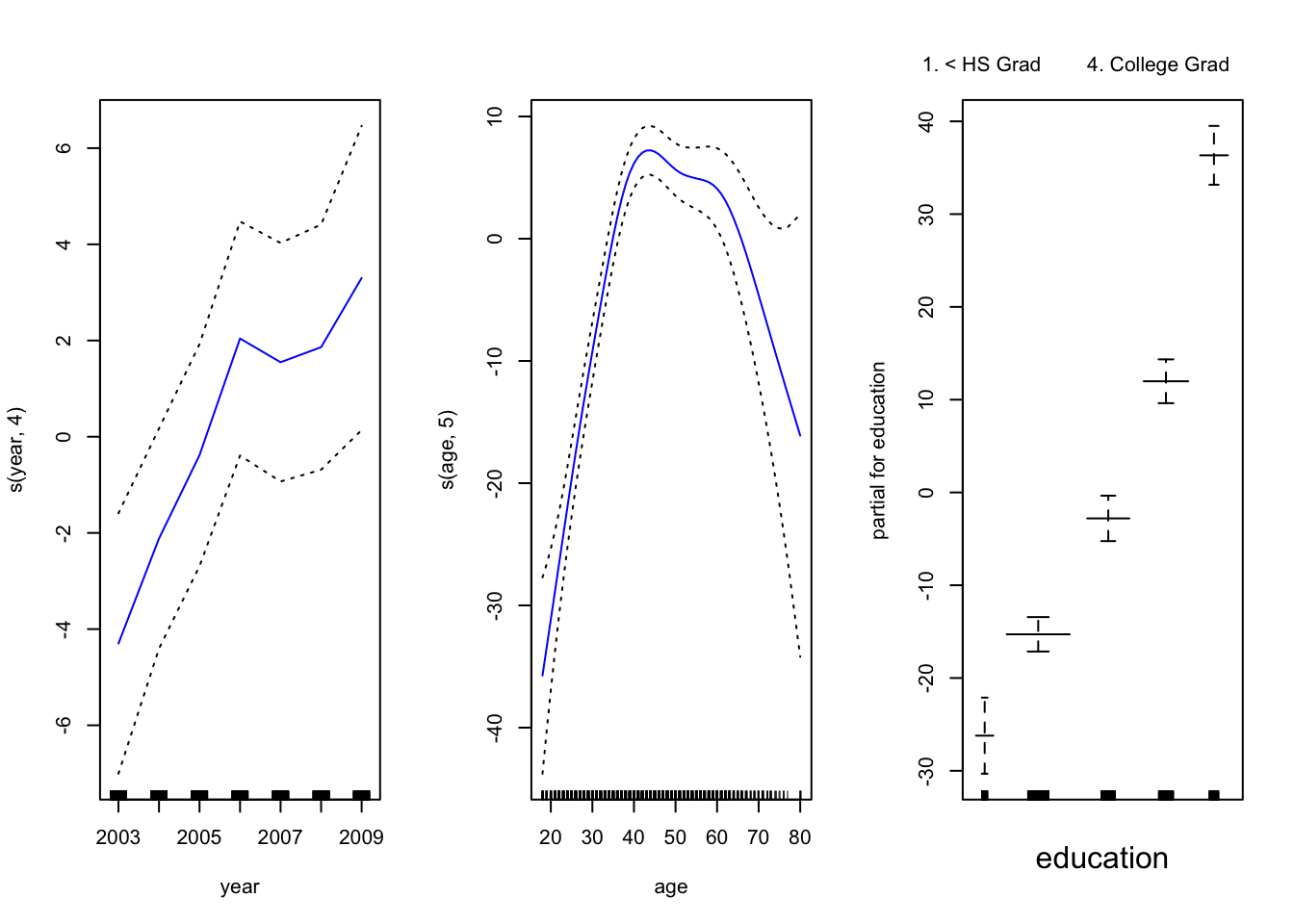
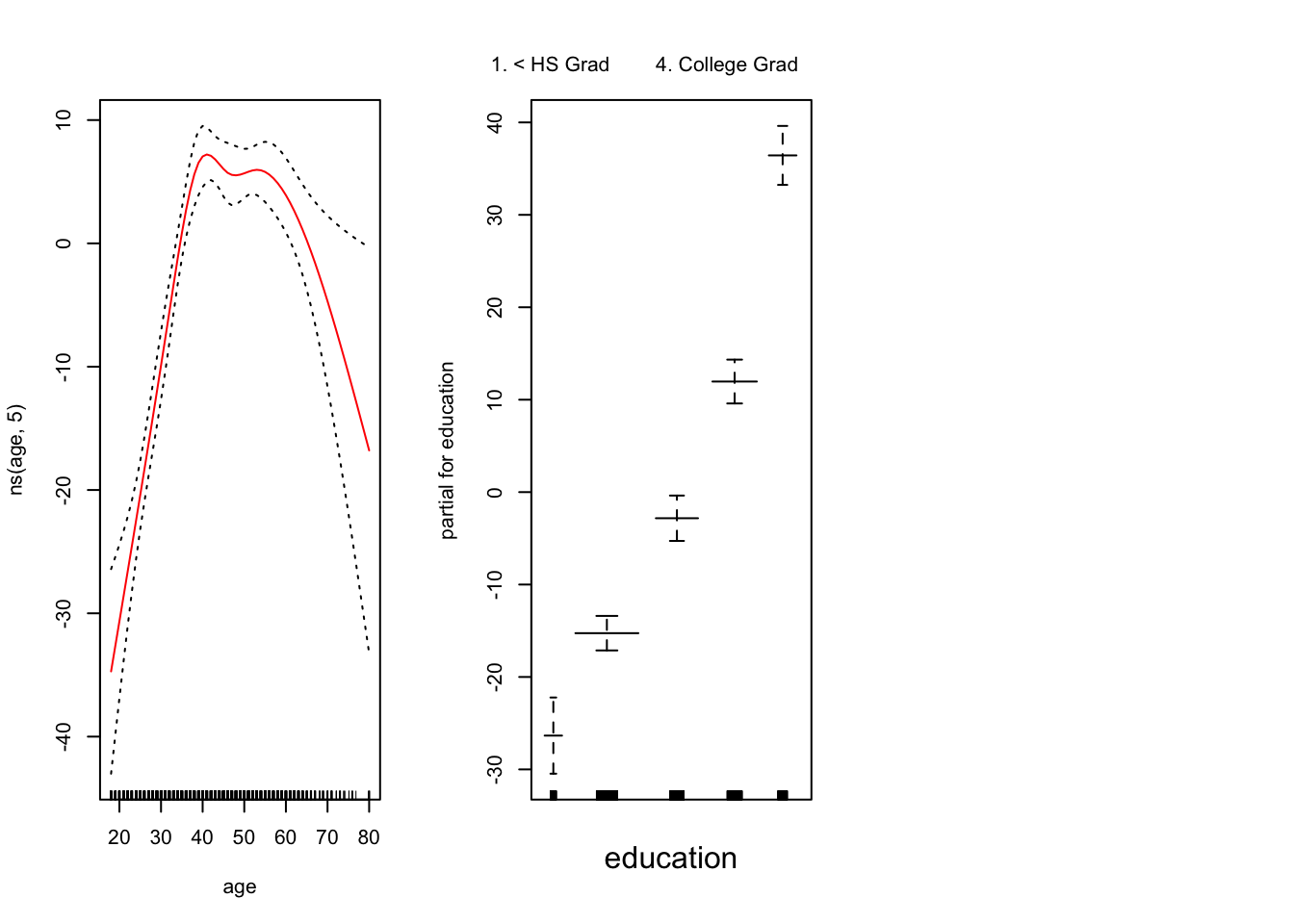
year 是线性的。我们可以创建一个新模型,然后使用ANOVA检验 。
## Analysis of Variance Table
##
## Model 1: wage ~ ns(age, 5) + education
## Model 2: wage ~ year + s(age, 5) + education
## Model 3: wage ~ s(year, 4) + s(age, 5) + education
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 2990 3712881
## 2 2989 3693842 1 19040 15.4 8.9e-05 ***
## 3 2986 3689770 3 4071 1.1 0.35
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
似乎添加线性year 成分要比不添加线性 成分的GAM好得多。
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -119.43 -19.70 -3.33 14.17 213.48
##
## (Dispersion Parameter for gaussian family taken to be 1236)
##
## Null Deviance: 5222086 on 2999 degrees of freedom
## Residual Deviance: 3689770 on 2986 degrees of freedom
## AIC: 29888
##
## Number of Local Scoring Iterations: 2
##
## Anova for Parametric Effects
## Df Sum Sq Mean Sq F value Pr(>F)
## s(year, 4) 1 27162 27162 22 2.9e-06 ***
## s(age, 5) 1 195338 195338 158 < 2e-16 ***
## education 4 1069726 267432 216 < 2e-16 ***
## Residuals 2986 3689770 1236
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Anova for Nonparametric Effects
## Npar Df Npar F Pr(F)
## (Intercept)
## s(year, 4) 3 1.1 0.35
## s(age, 5) 4 32.4 <2e-16 ***
## education
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
在具有非线性关系的模型中, 我们可以再次确认year 对模型没有贡献。
接下来,我们 将局部回归拟合GAM 。
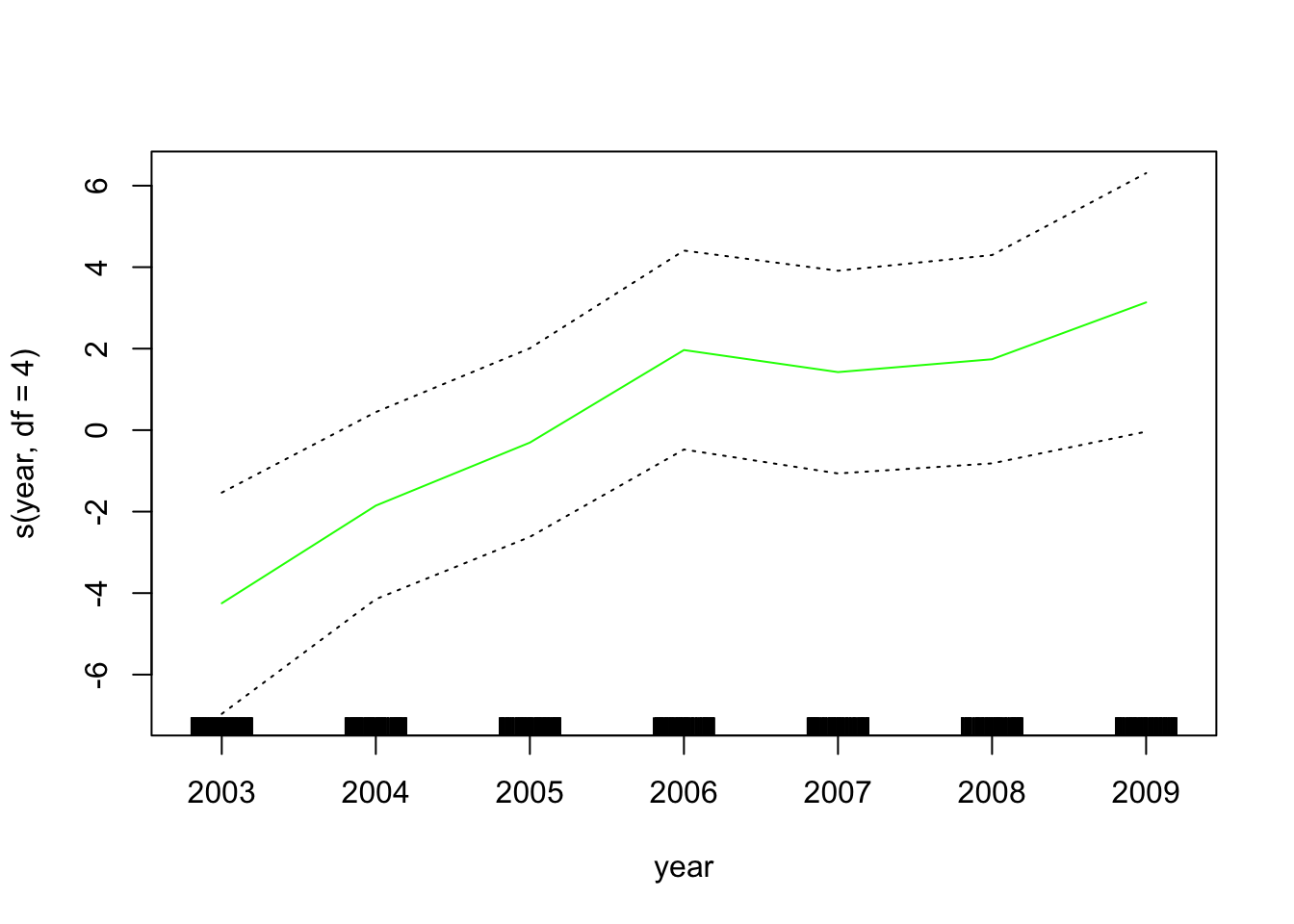
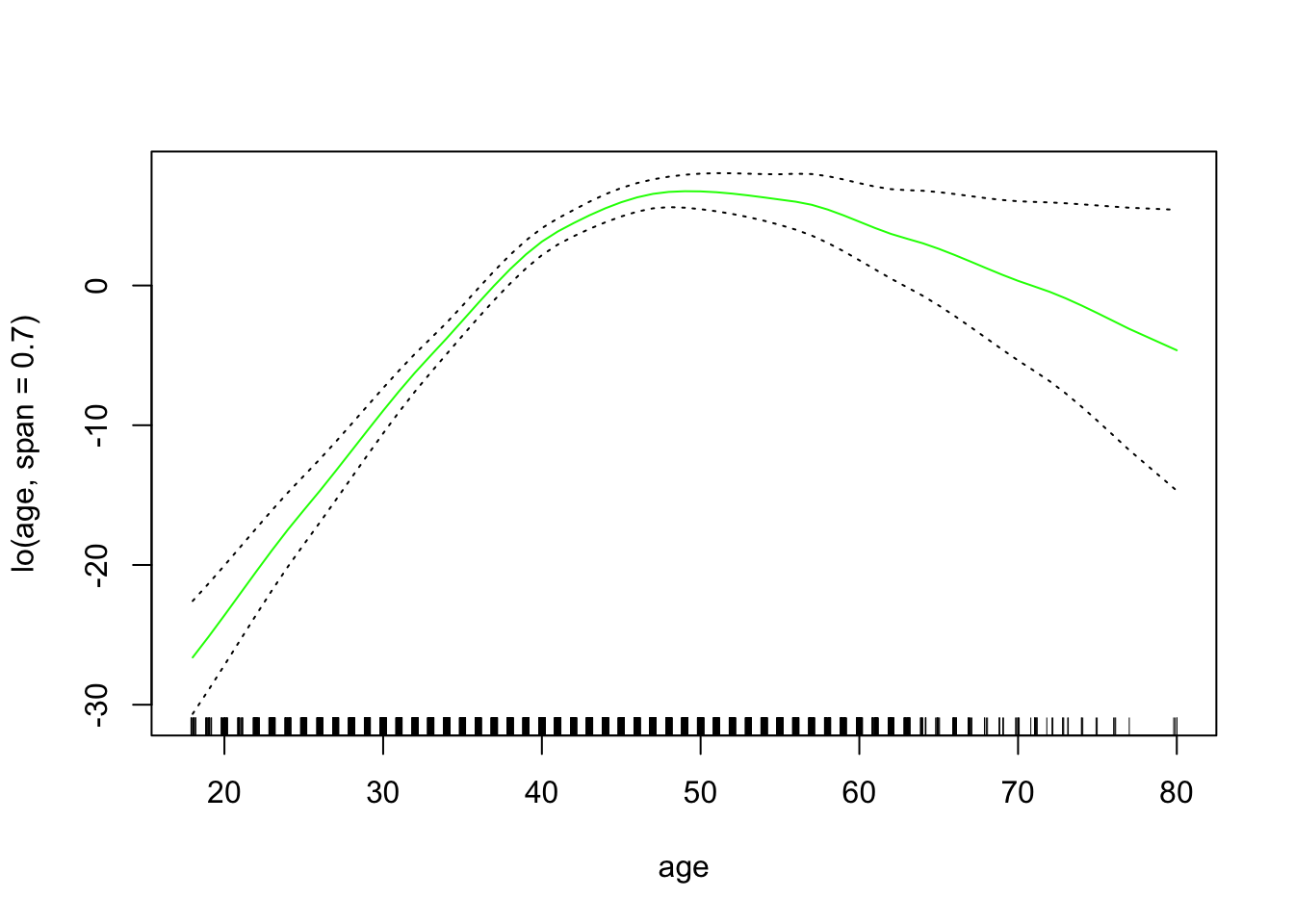
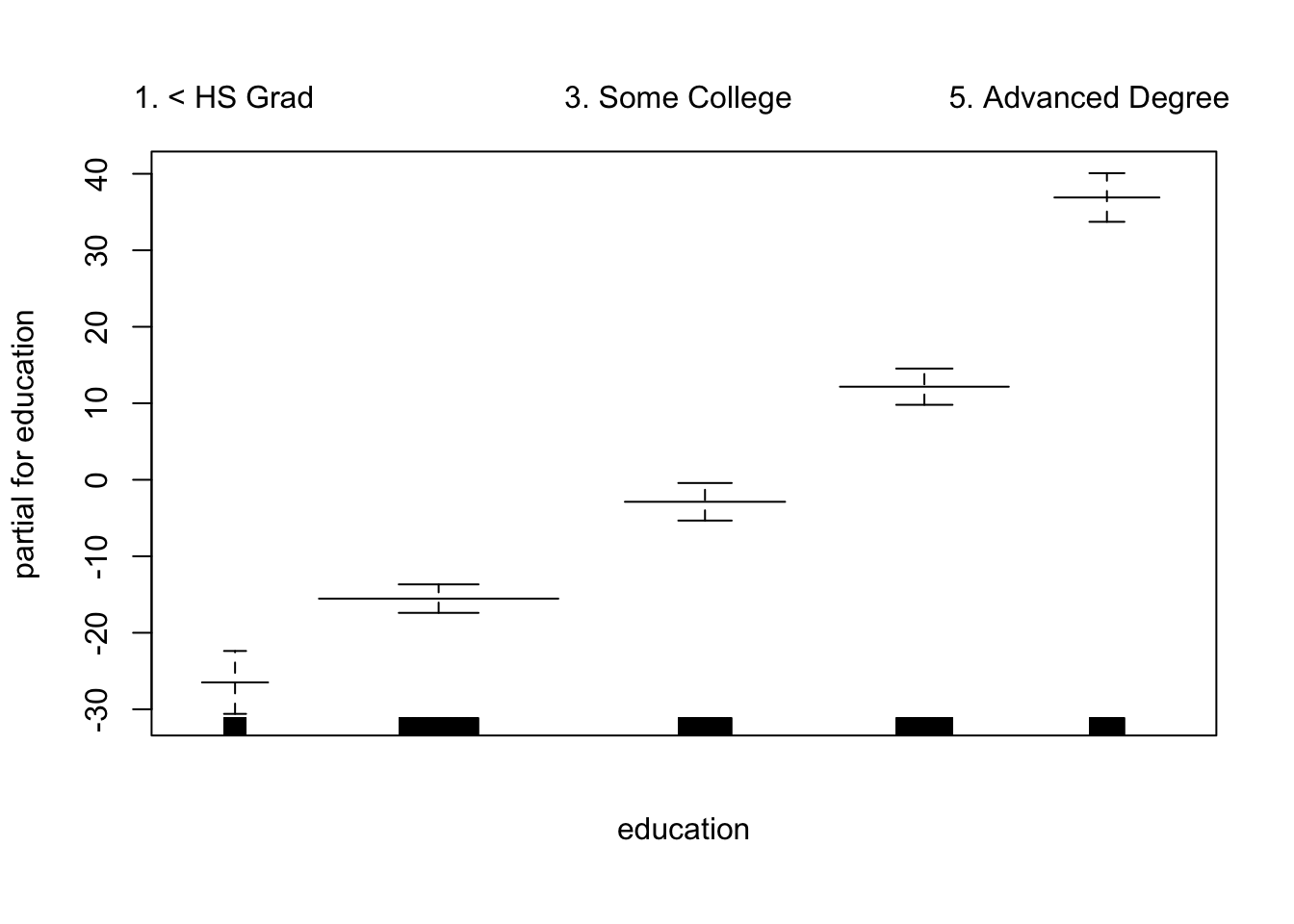
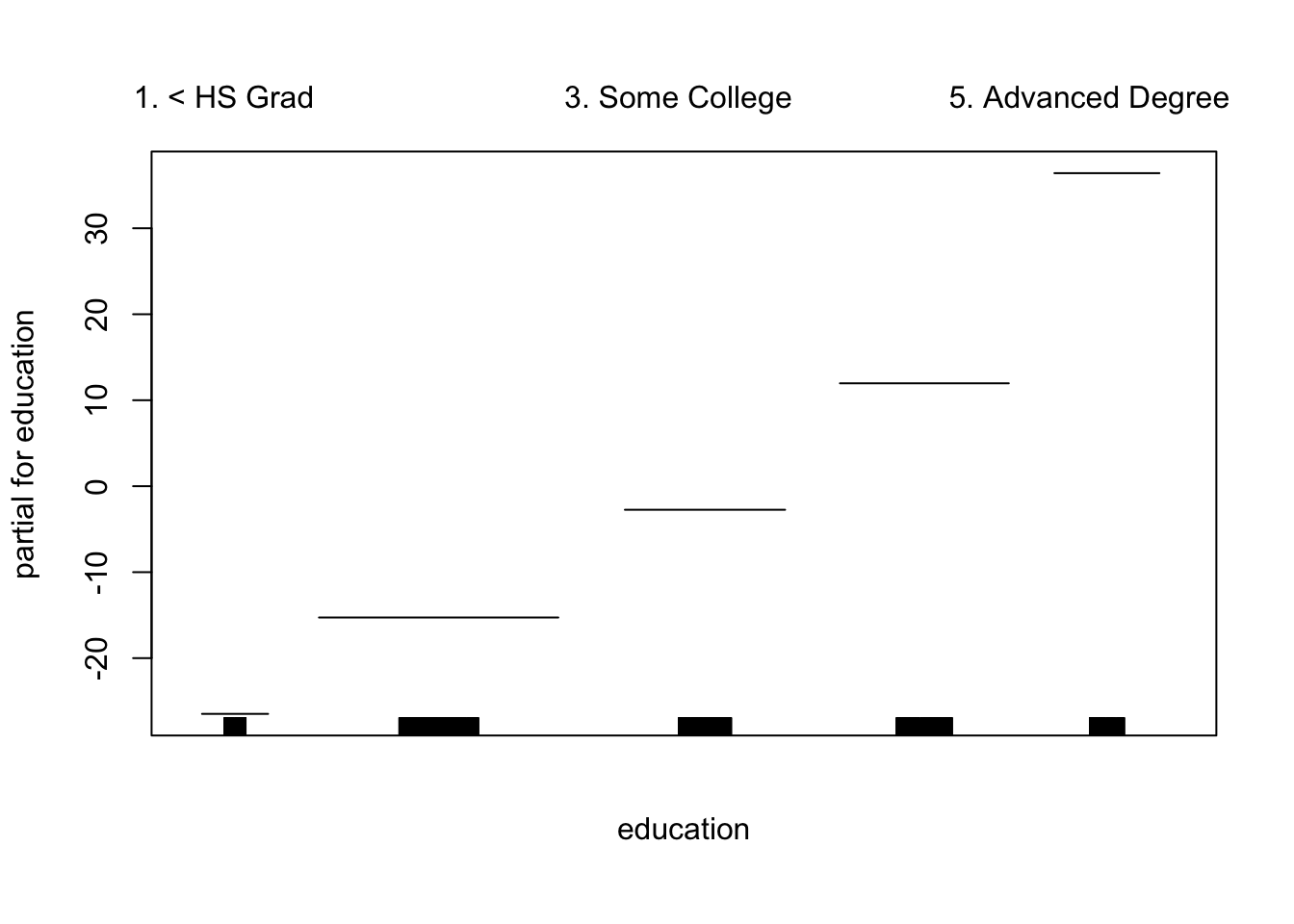
在调用GAM之前,我们还可以使用局部回归来创建交互项。
我们可以 绘制结果曲面图 。




![[附源码]Python计算机毕业设计宠物托管系统Django(程序+LW)](https://img-blog.csdnimg.cn/355754ef1c134d228f34474feb6f3800.png)
![[网络工程师]-网络安全-数字签名和数字证书](https://img-blog.csdnimg.cn/95047bafd6834fc8b89d234959835428.png)





![[附源码]JAVA毕业设计医院门诊挂号系统(系统+LW)](https://img-blog.csdnimg.cn/6681e679f1924ad09c22dd2f57c027b5.png)