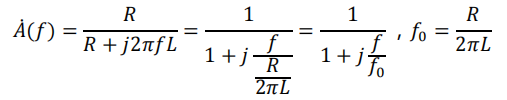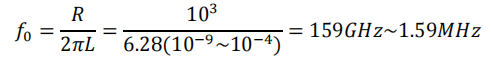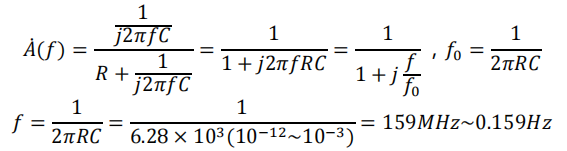前言：作为一个物联网的小辣鸡，硬件设计水平不能说没有，只能说一点点。
正好要做新项目，自己学着去处理信号，滤波，在这里做一点笔记。
参考书一：杨建国老师《新概念模拟电路》.pdf
参考书二：单电源运放图集.pdf(原版,翻译中文版)
注：想要的自己百度，实在找不到再伸手。下面提到的书一书二，对应的就是这上面的书。

一， 滤波器

滤波：是一个动作，对不同频率输入信号，实施不同的增益和相移，以形成输出。
模拟滤波，只能通过硬件电路实现。而数字滤波，既可以用硬件的数字电路实现，也可以用软件编程实现。

1.1 名词概念

1.1.1 高通滤波器

输入频率较高时，其增益逼近一个设定值，相移基本为 0，当输入频率低于某一设定值后，随着频率的降低，增益开始逐渐下降，相移开始逐渐增大，最终的结果是，直流量或者超低频率量，都会被滤除。

1.1.2 数字滤波器

输入量是离散的数字信号，或者是一个程序，对已有的数字序列进行滤波，形成新数据。例如:
原始数据为 X : [X0,X1,X2,…Xn,…] ，通过以下程序形成 Y[Y0,Y1,Y2 ,…Yn , …]

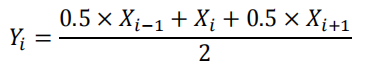
这就形成了一个数字滤波程序，实现了最简单的低通滤波效果。X 序列中存在的尖锐变化，会在输出的Y 序列中得到钝化。

1.1.3 无源滤波器(passive filter)

只用无源器件组成的滤波器。特点是无需外部供电即可工作，一般包括电阻、电容、电感和变压器。
无源滤波器的优点是:
1)在大电压、电流时，很多有源器件会失效，而无源器件一般不受限制
2)在超高频率时，无源器件具有天生的优势
3)实现最为简单的滤波时，无源电路有优势
4)一般来说，会比有源器件便宜一些，除非用到大个头的电感、电容.

1.1.4 有源滤波器(active filter)

是必须有额外电能供应才能工作的器件，比如晶体管、运放、门电路、处理器等。由至少 1 个有源器件组成的滤波器，称为有源滤波器。
有源滤波器的优点是:
1)可以引入负反馈、可以引入放大环节，因此可以实现极为复杂的滤波器，且能轻松应对小信号。
2)可以轻松实现多级滤波器的级联，而无源滤波器各级之间的互相影响是极为复杂的多级级联非常困难
3)对超低频率，有源滤波器有天生优势。它可以利用反馈网络，通过密勒等效等方法，用很小的电容代替超大电容、电感。我们知道，特征频率越低，要求电容值越大。即便现在已经有了超级电容，我们仍应坚信，制作电容需要足够大的面积和足够小的间距，这在物理上，是受限的。单纯用无源电路，想实现超低频率的滤波器，唯一的方法是使用超大的电容器，这非常困难。
4)电路计算相对更简单

1.1.5 传递函数A(S) S是复数(频率瞬态分析的实部…，稳态分析的虚部jw)

表示系统的频率特性。
是一个系统的输出时域函数Uo(t)的拉氏变换 Uo(S)，与输入时域函数Ui(S)的拉氏变换 Ui(S)的比值。
(好像是输入输出的频率关系，因为是个复数，所以比较麻烦，详见书一78-4)。

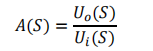
分析公式：电路中的电阻仍为R，电容写成1/SC，电感写成SL，然后用虚短虚断法，写出增益的 S域表达式，即为传函。
S域：表达式中的S，是一个复数频率，即包含瞬态分析的实部，也包含稳态分析的虚部jw：

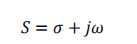
因此，S 域分析也称为复频域分析。
对于滤波器来讲，多数情况下我们只关心其稳态表现，即持续输入一个稳定正弦波输出也将是一个稳定正弦波，我们研究它们之间的幅度差异以及相移。此时，可以用S = jw代入。

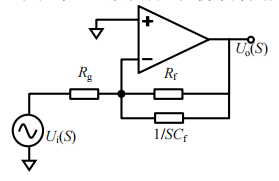
个人理解：下图是一阶低通滤波器，传递函数A(S)=Uout(S)/Uin(S)。因为流过Rg的电流等于Rf和Cf的电流，所以下面第三四五步。1/SCf是电容的阻值(应该是)。带入S = jw，得到下图右边的这个。

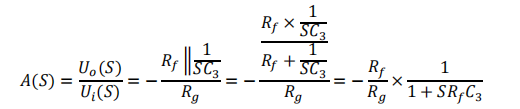
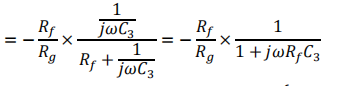
1.1.6 滤波器阶数的概念(Am：中频增益)

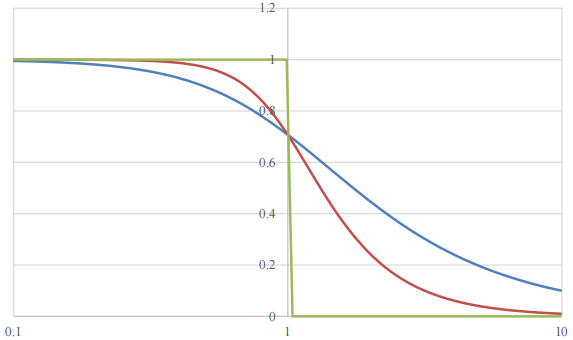
滤波器阶数越高，约接近于理想砖墙式滤波器(直来直去的一堵墙)。
下图绿色是理想的砖墙低通，蓝色是一阶低通滤波器的幅频特性，而红色是某个二阶滤波器的幅频特性。

上面这个1.5里的图就是一个一阶低通滤波器。表达式：

个人理解：在后面的时候我回头看才知道(大概)：Am=-Rf/Rg a=R x C

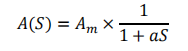
1.1.7 截止频率fL fH和特征频率fo=1/2ΠRC

fH：低通滤波器的上限截止频率
在低通滤波器中，随着频率的增大，增益的模开始下降，当增益的模变为中频增益的1/根号2，即 0.707 倍时，此时的频率称为低通滤波器的上限截止频率。
fL：高通滤波器的下限截止频率
在高通滤波器中，随着频率的减小，增益的模开始下降，当增益的模变为中频增益的1/根号2，即 0.707 倍时，此时的频率称为高通滤波器的下限截止频率。
fo：特征频率
特征频率是传函中较美的频率点，即在数学上，它是使得传函最简单的点。
一阶、三阶等奇数阶滤波器，传函中的分母上，实部和虚部相等的频率点，称为特征频率。其特征为，奇数阶滤波器的相移依次为正负45°，正负135°。
二阶、四阶等偶数阶滤波器，传函中的分母上，实部为 0 的点，或者虚部为 0 的点，称为特征频率。其特征为，偶数阶滤波器的相移依次为:正负90°，正负180°。
定义特征频率的相移规则为:阶数每增加 1 阶，对于低通，特征频率点处的相移顺时针转动 45°，即在原有滤波器基础上，再滞后 45。对于高通，则逆时针转动 45”，即在原有滤波器基础上，再超前 45°。

仅在巴特沃斯型滤波器中，特征频率等于截止频率。

1.1.8 中心频率fc

在窄带通和陷波器中，存在中心频率。
窄带通滤波器中，增益最大值处，或者相移为 0 度或者 360 度的整数倍时的频点，称为中心频率。
陷波器中，增益最小值处，或者相移为 0 度或者 360 度的整数倍时的频点，称为中心频率。
窄带通和陷波器都只能用偶数阶滤波器实现。
对于窄带通来说，传函分母为 0，即传函的极点，是发生增益最大的唯一位置，此时一定有相移为 0 或者 360 度整数倍的特性。
对于陷波器，传函的分子为 0，即传函的零点，是发生增益最小的唯一位置。
当然，这是理想情况，实际滤波器中，永远无法出现零点和极点。

1.2 电路分析

因为公式太多，实际没啥卵用，下面所以分析尽量只贴图电路和结论，看过程的在书一。

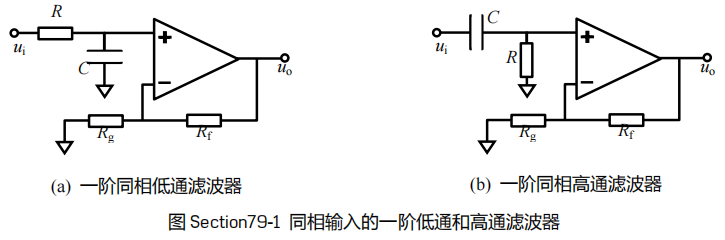
1.2.1 同相输入的一阶低通和高通滤波器

个人理解公式：
Uo=(1+Rf/Rg)U+ //U+是运放正极电压。虚短：U+=U-
U+=UiR/(R+Rc) //Rc是C的阻值
A(S)=Uo(S)/Ui(S)=(1+Rf/Rg)U+(S)/Ui(S)=(1+Rf/Rg) x Ui x R/(R+Rc)(S)/Ui(S)
约去Ui(S),就是下面这个传函。妈的，绝了，我想了半个钟才想到，写都写了为什么只写一半。可能是我自己蠢吧。
复数表达式中：1+aS=1+RCjw=1+jw/w0=1+jf/fo；//角频率：ω = 2πf

增益的模呈现规律为：

1. 频率极低时，增益近似为Am，低通。
2. 随着频率逐渐增大到f =f0，增益变为 0.707Am，此频率为截止频率，也是特征频率。
3. 此后，随着频率的再增大，增益会以-20dB/10 倍频的速率逐渐下降。
4. 非常巧的是，在这个电路中，特征频率恰好就是截止频率。

相位：在低频处，相移几乎为 0，在特征频率处，相移为-45°，随着频率的再增大，相移逐渐逼近-90°。

个人理解，如其名，频率小低通，频率大衰减，中间刚好是f0,也就是特征频率。fo=1/2ΠRC
频率越小相移越小，最大-90°。
低通高通差不多，反过来的。
例子不贴了，自己去看自己做的计算文档。(这是跟我自己说的)

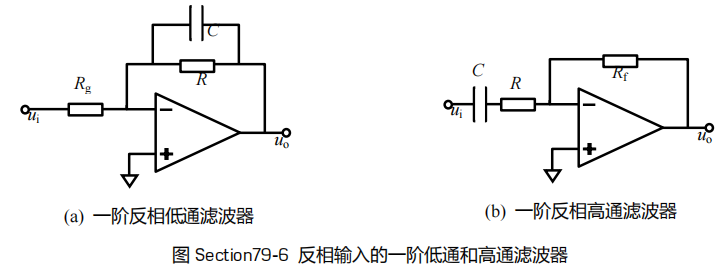
1.2.2反向输入的一阶低通和高通滤波器

个人理解公式：
C的阻值：1/SC =1/jwc=1/2Πfc //S=jw w=2Πf
例子不贴了，自己去看自己做的计算文档。(这是跟我自己说的)

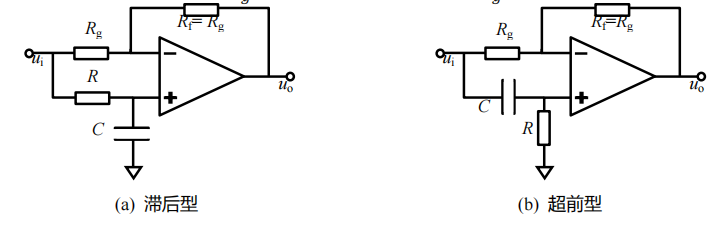
1.2.3 一阶全通滤波器

个人理解公式：
将R，C看作分压电阻，得出U+的电压。
因为U+=U-(虚短)，又因为Rg的电流和R的电流相同，写出节点电压法方程。

1.3 思考与总结

1.3.1 运放的滤波电路中，为什么用电容不用电感

运放组成的滤波器电路中，绝大多数甚至全部，都选择电容作为储能器件，而很少使用电感。这是为什么?

个人理解：
原理1：低频时，对 LR 型，电感感抗远远小于电阻值，增益为 1;对 RC 型，电容容抗远大于电阻值，增益为 1。要求低频时电感具有极小的等效导通电阻，电容应用极大的漏电阻。
原理2：高频时，对 LR 型，电感的感抗远大于电阻值，增益接近于 0;对 RC 型，电容容抗远小于电阻值，增益接近于0。要求电感的漏电阻应很大，电容等效导通电阻应很小。
原理3：极高频率和极低频率之间的中频段，也就是特征频率或者截止频率发生的频段此时，应有感抗和容抗都和电阻值接近。
原理4：滤波器中的电阻值，不是任意选择的。为了保证运放输出电流不要太大，电阻值不能选择太小的，10V/10R=1A，而从噪声考虑，电阻又不能过大，因此100Q~100kQ 是常见选择，而选择 1kR 是普适安全的。

论证：如果电阻为1kR，特征频率的范围取决于电感量。一般来说，受限于制造难度，多数电感值在 1nH-100mH 之间。即多数电感能够工作的特征频率区间，大约于 159MHz-159GHz。而一般运放的工作频率区间是 0Hz~100MHz。

论证：常见电容器的容值一般为 1pF~1000uF，其特征频率可以发生在 0.159Hz-159MHz，与运放的工作频率相吻合。

结论：电感构成的滤波器，多数情况下，只能工作在截止频率较大的场合。而这个频率区间与运放的工作区间非常不吻合。