强化学习QLearning 进行迷宫游戏和代码

强化学习是机器学习里面的一个分支。它强调基于环境而探索行动、学习，以取得最大化的预期收益。其灵感来源于心理学中的行为主义理论，既有机体如何在环境给予的奖励或者惩罚的刺激下，逐步形成对刺激的预期，产生能够最大利益的习惯性行为。简而言之，强化学习就是让机器学着如何在环境中通过不断的试错、尝试，学习、累积经验拿到高分.

强化学习基本结构

强化学习致力于控制一个计算机智能体，使之在未知环境中完成任务目标。

下图中给出强化学习基本机构。在一个未知“迷宫”环境中，计算机算法软件（探索机器人控制大脑）基于自身的控制策略行动。基本结构包括：

（1）智能体（Agent）：探索机器人大脑，智能体的结构可以是一个神经网络，也可以是一个简单的算法，智能体的输入通常是状态（State），输出通常是策略（Policy）；

（2）动作(Actions)：是指动作空间。对于机器人玩迷宫游戏，只有上下左右移动方向可行动，那Actions就是上、下、左、右；

（3）状态(State)：就是智能体的输入，机器人在迷宫中的位置；

（4）奖励(Reward)：机器人进入某个状态时，能给智能体带来正奖励或者负奖励；

（5）环境（Environment）：就是指机器人所走的迷宫，能接收action，返回state和reward。

1、强化学习决策过程

马尔科夫决策过程（MDP）为求解强化学习问题提供了数学框架。几乎所有的强化学习问题都可以建模为MDP。

在强化学习中，agent与environment按顺序在互动。在时刻 t1 ，agent会接收到来自环境的一个observation（观察），获取状态s1，基于这个状态s1 ，agent会做出动作a1 ，然后这个动作作用在环境上，于是agent可以接收到一个奖赏rt+1，并且agent就会到达新的状态s2，以此方式持续下去。agent与environment之间的交互就是产生了一个序列，如下图所示。

强化学习迷宫Q-Learning算法决策实现过程，就是马尔科夫决策过程（MDP）过程的实现，实践过程如下图所示。

强化学习基本要素

基于上述迷宫的案例，我们可以整理出思路里面出现的强化学习要素：

2.4.1. 马尔可夫决策过程（MDP）模型要素

马尔可夫决策过程（MDP）包含5个模型要素，状态（state）、动作（action）、策略（policy）、奖励（reward）和回报（return）：

（1）环境的状态s，状态是对环境的描述，正如机器人在迷宫中的位置，也就是t时刻环境的状态st，体现为环境状态集中的某一个状态，在智能体做出动作后，状态会发生变化；MDP所有状态的集合是状态空间，状态空间可以是离散或连续的。

S= s1，s2，s3，s4，……,sπ

（2）机器人的动作A,动作是对智能体行为的描述，是智能体决策的结果。t时刻机器人采取的动作At,是它的动作集中某一个动作；MDP所有可能动作的集合是动作空间，动作空间可以是离散或连续的。

A= a1，a2，a3，a4，……,aπ

（3）环境的奖励R，奖励是智能体给出动作后，环境对智能体的反馈。是当前时刻状态、动作和下个时刻状态的标量函数。

t时刻机器人在状态st ,采取的动作at对应的奖励rt+1 ，会在t+1时刻得到；

R = R(st， at，st+1)

（4）机器人的策略（policy）π，策略是指代表机器人采取动作的依据，即机器人会依据策略π来选择动作。最常见的策略表达方式是一个条件概率分布π（a|s）, 即在状态s时采取动作a的概率。即π（a|s）=P（At = a| st=s），此时概率大的动作被机器人选择的概率较高。

（5）环境的状态转化模型，可以理解为一个概率状态机，它可以表示为一个概率模型，即在状态s下采取动作a ，转到下一个状态s’的概率，表示为Pass’ 。

2.4.2. 贝尔曼方程及其要素

贝尔曼方程（Bellman Equation）也被称作动态规划方程（Dynamic Programming Equation），用于求解马尔可夫决策过程（MDP）过程。

贝尔曼方程是动态规划（Dynamic Programming）这些数学最佳化方法能够达到最佳化的必要条件。此方程把“决策问题在特定时间怎么取值”以“来自初始选择的报酬比从初始选择衍生的决策问题的值”的形式表示。借此这个方式把动态最佳化问题变成简单的子问题，而这些子问题遵守从贝尔曼所提出来的“最优原理”。

几乎所有的可以用最优控制理论（Optimal Control Theory）解决的问题也可以通过分析合适的贝尔曼方程得到解决。然而，贝尔曼方程通常指离散时间（discrete-time）最佳化问题的动态规划方程。

贝尔曼方程的三个要素，策略函数、状态价值函数、状态——行为值函数（Q函数）（简称为动作价值函数）。

（1）回报（return），回报是奖励随时间步的积累，在引入轨迹的概念后，回报也是轨迹上所有奖励的总和。

（2）折扣因素，奖励衰减因子（γ），在[0,1]之间。如果为0，则是贪婪法，即价值只由当前延时奖励决定，如果是1，则所有的后续状态奖励和当前奖励一视同仁。大多数时候，我们会取一个0到1之间的数字，即当前延时奖励的权重比后续奖励的权重大。

折扣因素主要作用：

避免连续任务造成回报G无限大；

区分即时奖励和未来奖励的重要程度。

（3）状态值函数机器人在策略π和状态s时，采取行动后的状态所处的最佳的（程度）价值（value），一般用表示，是一个期望函数。

价值函数一般可以表示为下式，不同的算法会有对应的一些价值函数变种，但思路相同：

（4）状态——行为值函数（Q函数）

机器人在策略π和状态s时，采取行动后的行为的所处的最佳的程度，一般用表示，也是一个期望函数。

根据策略π从状态s 开始采取行动a所获得的期望回报，也就是贝尔曼方程，如下式所述：

（5）探索率ϵ，这个比率主要用在强化学习训练迭代过程中，由于我们一般会选择使当前轮迭代价值最大的动作，但是这会导致一些较好的但我们没有执行过的动作被错过。因此我们在训练选择最优动作时，会有一定的概率ϵ不选择使当前轮迭代价值最大的动作，而选择其他的动作。

Q-Learning算法

时序差分学习 (temporal-difference learning, TD learning)：指从采样得到的不完整的状态序列学习，该方法通过合理的 bootstrapping，先估计某状态在该状态序列(episode)完整后可能得到的 return，并在此基础上利用累进更新平均值的方法得到该状态的价值，再通过不断的采样来持续更新这个价值。

时间差分(TD) 学习是蒙特卡罗(MC) 思想和动态规划(DP) 的结合。与MC方法类似，TD方法可以直接从经验中学习，而不需要知道环境模型。与 DP 类似，TD方法基于其他学习的估计值来更新估计值，而不用等待最终的结果。首先从预测(prediction)问题出发，建立给定策略 [公式] 对应的值函数 [公式] 的估计。对于控制(control)问题，DP、TD以及MC方法都使用了广义策略迭代(GPI)的某种形式。这些方法中的不同点主要体现在解决预测问题方面。

Q-learning一种TD（Time Difference）方法，也是一种Value-based的方法。所谓Value-based方法，就是先评估每个action的Q值(Value)，再根据Q值求最优策略的方法。

在Q -值函数包含了两个可以操作的因素。

首先是一个学习率 learning rate（α），它定义了一个旧的Q值将从新的Q值哪里学到的新Q占自身的多少比重。值为0意味着代理不会学到任何东西（旧信息是重要的），值为1意味着新发现的信息是唯一重要的信息。

下一个因素被称为折扣因子discount factor（γ），它定义了未来奖励的重要性。值为0意味着只考虑短期奖励，其中1的值更重视长期奖励。

公式可以变换为：

因此：

是指旧Q值在newQ（s,a）之中所占得比重

是指为本次行动学习到的奖励（行动本身带来的奖励和未来潜在的奖励)。

3.3. Q-table

Q-Learning最终目标是获得回报G，这样需要保存训练过程中的轨迹上所有奖励的总和。因此设计了Q-table用于存储Q（s,a），创建一个二维表，可以存储每个state中每个action的未来预期的最大奖励值。这样我们可以知道每个state下的最佳action。

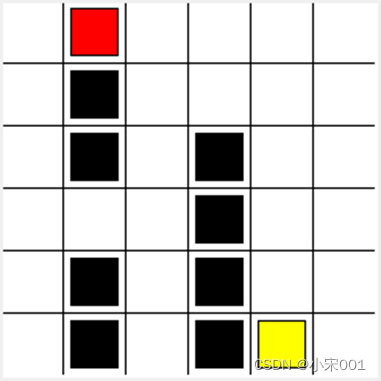
如下图迷宫，每个state（这里指的是方块）允许四种可能性的action，即上、下、左、右。

这个table就叫做Q-table（Q指的是这个action的预期奖励）。迷宫的Q-table中的列有四个action（上下左右行为），行代表state，每个单元格的值将是特定状态（state）和行动（action）下未来预期的最大奖励值

4. 迷宫游戏代码结构

迷宫游戏代码有三部分组成：

maze_env 是迷宫环境，基于Python标准GUI库Tkinter开发

RL_brain 是Q-Learning的核心实现

run_maze 是控制执行算法的代码

maze_env.py

import numpy as np
import time
import sys

sys.setrecursionlimit(10000)
if sys.version_info.major ==2:
    import Tkinter as tk
else:
    import tkinter as tk
UNIT = 40 #像素
MAZE_H = 6 #网格高度
MAZE_W = 6 #网格宽度

class Maze(object):
    def __init__(self):
        self.action_space = ['u','d','l','r']
        self.n_actions = len(self.action_space)
        # self.title('迷宫')
        # self.geometry('{0}x{1}'.format(MAZE_H*UNIT,MAZE_W*UNIT))
        # 初始化窗口 画布
        self.window = tk.Tk()
        self.canvas = tk.Canvas(self.window,bg='white',
                                height= MAZE_H*UNIT,
                                width = MAZE_W*UNIT)
        self._build_maze()
    def _build_maze(self):
        h = MAZE_H * UNIT
        w = MAZE_W * UNIT
        #创建画布，设计宽和高
        #创建栅格
        # 画线
        for c in range(0, w, UNIT):
            self.canvas.create_line(c, 0, c, h)
        for r in range(0, h, UNIT):
            self.canvas.create_line(0, r, w, r)
        # 陷阱
        self.hells = [
            self._draw_rect(3, 2, 'black'),
            self._draw_rect(3, 3, 'black'),
            self._draw_rect(3, 4, 'black'),
            self._draw_rect(3, 5, 'black'),
            self._draw_rect(4, 5, 'black'),
            self._draw_rect(1, 0, 'black'),
            self._draw_rect(1, 1, 'black'),
            self._draw_rect(1, 2, 'black'),
            self._draw_rect(1, 4, 'black'),
            self._draw_rect(1, 5, 'black')
        ]
        self.hell_coords = []
        for hell in self.hells:
            self.hell_coords.append(self.canvas.coords(hell))

        # 奖励
        self.oval = self._draw_rect(4, 5, 'yellow')
        # 玩家对象
        self.rect = self._draw_rect(0, 0, 'red')
        self.canvas.pack()

    # color 颜色
    def _draw_rect(self, x, y, color):
        center = UNIT / 2
        w = center - 5
        x_ = UNIT * x + center
        y_ = UNIT * y + center
        return self.canvas.create_rectangle(x_ - w,
                                            y_ - w,
                                            x_ + w,
                                            y_ + w,
                                            fill=color)
    def reset(self):
        self.canvas.update()
        time.sleep(0.5)
        self.canvas.delete(self.rect)
        self.rect = self._draw_rect(0, 0, 'red')
        self.old_s = None
        return self.canvas.coords(self.rect)
        # return self.window.coords(self.rect)
    # 走下一步
    def step(self,action):
        s = self.canvas.coords(self.rect)
        base_action = np.array([0,0])
        if action == 0: #up
            if s[1]>UNIT:
                base_action[1] -=UNIT
        elif action == 1: #down
            if s[1] <(MAZE_H -1) * UNIT:
                base_action[1] += UNIT
        elif action == 2: #right
            if s[0] <(MAZE_W -1) * UNIT:
                base_action[0] += UNIT
        elif action == 3:  # left
            if s[0] >  UNIT:
                base_action[0] -= UNIT
        # 根据策略移动红块
        self.canvas.move(self.rect,base_action[0],base_action[1])
        s_ = self.canvas.coords(self.rect) #next state
        # 判断是否得到奖励或惩罚
        if s_ ==self.canvas.coords(self.oval):
            reward = 1
            done = True
            s_ = 'terminal'
        elif s_ in self.hell_coords:
            reward = -1
            done = True
            s_ = 'terminal'
        else:
            reward = 0
            done = False
        self.old_s = s
        return  s_,reward,done
    def rander(self):
        time.sleep(0.1)
        self.canvas.update()
def update():
    t=0
    for t in range(10):
        s = env.reset()
        print(s)
        while True:
            env.rander()
            a = 2
            s,r,done = env.step(a)
            t+=1
            # print(t)
            if done:
                break
if __name__ == '__main__':
    print(sys.getrecursionlimit())
    env = Maze()
    env.window.after(100,update)
    env.window.mainloop()

RL_brain.py 是Q-Learning的核心实现

import numpy as np
import pandas as pd

class QLearningTable:
    def __init__(self,actions,learning_rate=0.01,reward_decay=0.9,e_greedy=0.9):
        self.actions = actions
        self.lr = learning_rate
        self.gamma = reward_decay
        self.epsilon = e_greedy
        self.q_table = pd.DataFrame(columns=self.actions,dtype=np.float64)
        print(self.q_table)
    def choose_action(self,observation):
        self.check_state_exist(observation)
        if np.random.uniform()<self.epsilon:
            state_action = self.q_table.loc[observation,:]
            # 防止相同列值时取第一个列，所以打乱列的顺序
            action = np.random.choice(state_action[state_action==np.max(state_action)].index)
        else:
            action = np.random.choice(self.actions)
        return action
    def learn(self,s,a,r,s_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s,a] # q估计

        if s_ !='terminal':
            q_target = r + self.gamma*self.q_table.loc[s_,:].max() # q现实
        else:
            q_target = r
        self.q_table.loc[s,a]  += self.lr *(q_target - q_predict)
    # 检查状态是否存在
    def check_state_exist(self,state):
        if (state not in self.q_table.index):
            self.q_table = self.q_table.append(
                pd.Series(
                    [0]*len(self.actions),
                    index= self.q_table.columns,
                    name = state,
                )
            )

run_maze.py 是控制执行算法的代码

from maze_env import Maze
from QLearn.RL_brain import QLearningTable
import numpy as np
def update1():
    for episode in range(100):
        #获取初始坐标
        observation = env.reset()
        # print(type(observation))
        print(observation)
        while True:
            # 刷新环境
            env.rander()
            #  Rl基于观测选择下一个动作
            action = RL.choose_action(str(observation))
            print(action)
            #  执行这个动作得到反馈（下一个状态observation_ 奖励reward 是否结束done）
            observation_,reward, done = env.step(action)
            # RL更新状态表Q-table
            RL.learn(str(observation),action,reward,str(observation_))
            observation = observation_
            if done:
                break

if __name__ == '__main__':
    env = Maze()
    RL = QLearningTable(actions=list(range(env.n_actions)))

    env.window.after(10,update1) # 设置10ms的延迟
    env.window.mainloop()

运行之后的效果图：