平面直角坐标系

回顾我们的数据可视化的学习历程，其实始于笛卡尔坐标系的创建，并由此建立了数与形的对应关系。在笛卡尔坐标系中随便点上一点，这个点天生具备坐标，从而与数对$(x,y)$完成映射，这就是最基础的散点图。将点连在一起，便是折线图。

但在matplotlib中，折线图反而比散点图更加基础，因为散点图至少需要两组一一对应的X和Y坐标，而折线图在只接受一组数据的情况下，便会默认自然数列为x坐标，从而绘图过程更加遍历

import numpy as np
import matplotlib.pyplot as plt
ys = np.arange(100)**2
plt.plot(ys)
plt.show()

空间直角坐标系

将曲线绘制在三维坐标系中的方法有两个，尽管从思维的角度出发，直接绘制比较方便，但从matplotlib的绘图逻辑来说，最简单的方案是把二维坐标系嵌入到三维坐标系中，换言之，为其指定一个额外的轴。

xs = np.linspace(0, 1, 100)
ys = np.sin(xs * 2 * np.pi) / 2 + 0.5

fig = plt.figure()
zs = ['x', 'y', 'z']
for i, z in enumerate(zs, 1):
    ax = fig.add_subplot(1,3,i, projection='3d')
    ax.plot(xs, ys, zs=0, zdir=z)
    ax.set_zlim(0,1)
    ax.set_xlim(0,1)
    ax.set_ylim(0,1)

plt.show()

在上面的代码中，调用的仍旧是plot，但是用zdir参数指定了z轴方向，当为z轴设置不同的方向时，曲线所嵌入到的三维直角坐标系的坐标平面是不同的。

很显然，这是个伪3D曲线，但plot函数是有实力绘制真正的三维曲线的，无非多一个坐标轴而已

xs = np.linspace(0, 5, 100)
ys = np.sin(xs * 2 * np.pi) / 2 + 0.5
zs = np.cos(xs * 2 * np.pi) / 2 + 0.5
ax = plt.subplot(projection='3d')
ax.plot(xs, ys, zs)
plt.show()

效果如下

极坐标

极坐标的建立与三维直角坐标系的建立是相同的，均以指定projection的形式实现

r = np.arange(0, 2, 0.01)
theta = 2 * np.pi * r
ax = plt.subplot(projection='polar')
ax.plot(theta, r)
plt.show()

绘图结果如下

在极坐标中绘图时，plot函数保留了默认自变量的功能，试验一下就清楚了

ax = plt.subplot(projection='polar')
ax.plot(r)
plt.show()

下图中，由于默认$\theta$的增长步长为1，这对于每圈$2\pi$的极坐标来说是非常大的一个量，故而图形在绘制过程中出现了不可避免的曲折。

但matplotlib并没有封装一个拿来就能用的柱坐标或者球坐标，除非自己在三维直角坐标系中实现一个。

地理坐标

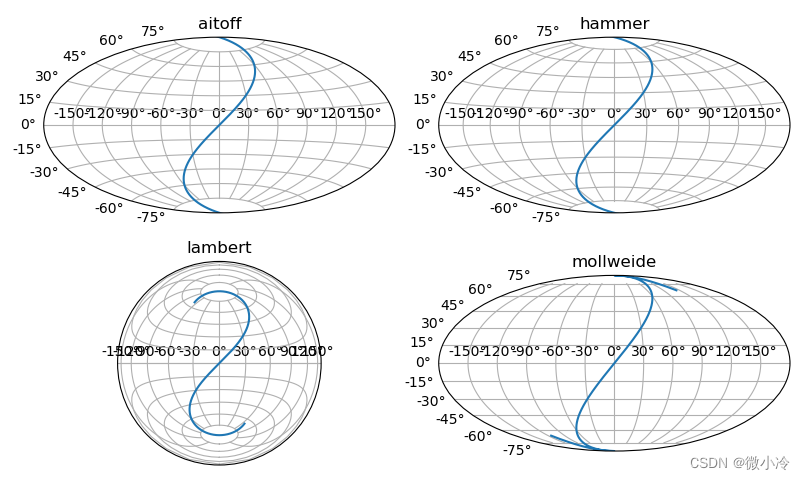
projection的含义是投影，除了3D坐标和极坐标之外，还支持多种地理坐标，例如汉迈尔-埃托夫投影等，下面就列举几个不同的地理坐标，并在其中进行

projs = ['aitoff', 'hammer', 'lambert', 'mollweide']
fig = plt.figure()
xs = ys = np.arange(-2,2,0.01)
for i, p in enumerate(projs, 1):
    ax = fig.add_subplot(2,2,i,projection=p)
    ax.plot(xs, ys)
    plt.title(p)
    plt.grid()

plt.show()