题目大意

mtc是一个很优秀的同学，他学习认真，经常刷题。这天，他正好学习到了数据离散化与二位前缀和的相关概念，并给大家进行科普.
数据的离散化:有些教据本身很大，自身无法作为数组的下标保存对应的属性，如果这时只是需要这堆数据的相对属性，那么可以对其进行离散化处理。当数据只与它们之间的相对大小有关，而与具体是多少无关时，可以进行离散化。百度百科
例如:设有4个数:
1234567、123456789、12345678、123456
排序:123456<1234567<12345678<123456789
=>1<2<3<4
那么这4个数可以表示成:2、4、3、1
实现离散化的方法有很多，大家可以自行学习
二维前缀和:定义一个二维数组s0，s川们表示二维数组中，左上角(1,1)到右下角,所包围的矩阵元素的和。如下图所示


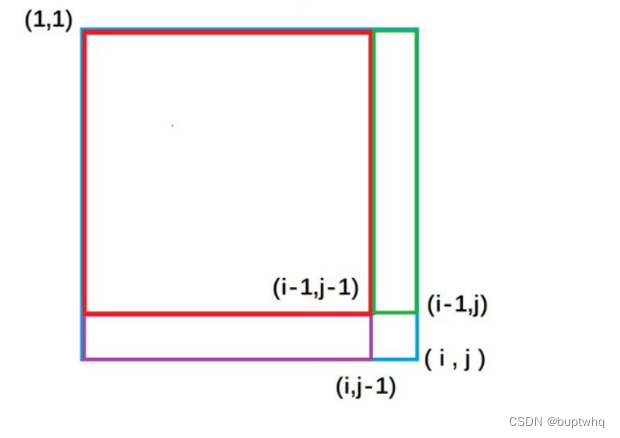
二维前缀和的推导公式:整个外围蓝色矩形面积s们=绿色面积S - 1]M] + 紫色面积 -1重复加的红色的面积 - 1-1]+小方块的面积a[ilij]。
使用二位前缀和求解矩阵的面积:求以(x1,y1)为左上角和以(2,y2)为右下角的矩阵的元素的和。

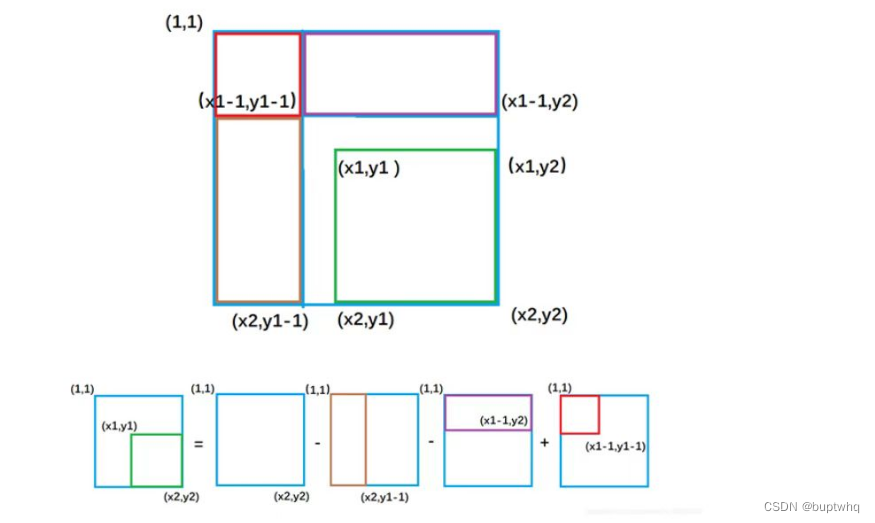
绿色形的面积 S= 整个外围面积[x2,2] -黄色面s2y1-11-紫色面1 -1,y2] +重复减去的红色面积 1 -1,y1 -11
当你认直听取m队长给你讲述的知识后，脑洞大开，决定利用所学内容解决下述问题。在一张无限大二维网格上，存在n(n<=5000个点，点i(0<=n)坐落在(y格子上。当我们任取两个点，都可以以这两个点构成一个矩形注意:当两个点横坐标相同或纵坐标相同时退化成一条宽为1的
网格条，两个点是同一坐标时退化成一个网格，这并不影响我们的任务)，我们的任务是求出这个矩形内存在多少个点?

输入

第一行输入两个整数n,m表示网格上分布着n个点，同时我们有m个矩形需要统计内部的点的数量
接下来n行，每行两个整数x,y表示点i(0<=i<n)的坐标。
接下来m行，每行两个整数k1,k2(0<=k1,k2n)，表示我们查询以点k1和点k2构成的矩形内点的数量

输出

m行，每行一个整数，表示第i次询问的矩形内部的点的数量
示例 1：

输入：
4 3
0 0
0 1
1 0
1 1
0 3
0 1
2 2
输出：
4
2
1

样例解释

一共四个点，分布在(0,0),(0,1),(1,0)11)四个网格中，如图所示:

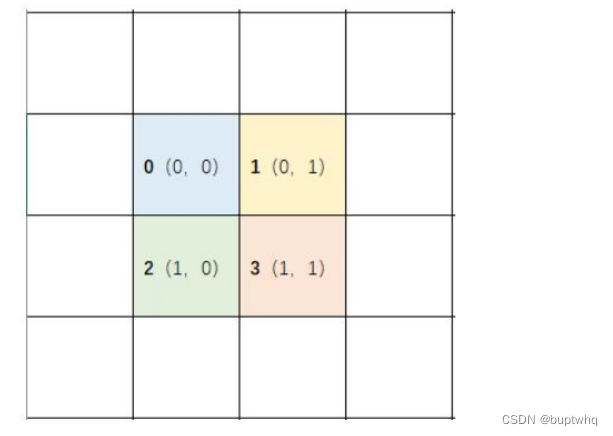
三次询问，0号点和3号点构成的矩形以(O,0)为左上角，(1,1)为右下角，内部包含4个点。
0号点和1号点构成的矩形以(0，0)为左上角， (0，1)为右下角，内部包含2个点。
2号点和2号点构成的矩形只有 (1，0)一个格子，内部包含1个点。

重要提示

保证60%的数据中，点的数量n<=100，查询的次数m<=100，并且所有点的坐标都在[1,100]以内，也就是说你完全可以不听取m队长的任何建议就可以得到本题目60%的分数。
保证80%的数据中，点的数量n<=5000，查询的次数m<=10000，并且所有点的坐标都在[1, 1000]以内，也就是说你只需要听会m队长的二维前缀和就可以得到本题目80%的分数。
保证100%的数据中，点的数量n<=5000，查询的次数m<=100000，并且所有点的坐标在int表示的范围内即[-2^31, 2^31-1]，也就是说你既需要学会m队长讲的离散化也要学会二位前缀和才可以得到本题目100%的分数。

思路

非常经典的值域大而数据数量少的问题，可采用离散化方法；而多次查询，可采用前缀和思想预先处理，节约每次查询的时间。
离散化+二维前缀和，详见代码注释。
其中数据范围通过点的数量和查询次数来确定，每次查询是选择某个点，而点数n最多为5000，因此横坐标、纵坐标最多都为5000，确定了离散化后的数组维度N与n相同。

代码

#include <bits/stdc++.h>

using namespace std;

int n, m;
const int N = 5000 + 10;
int a[N][N], s[N][N]; // 离散化后的点数组、前缀和数组
vector<vector<int>> point; // 存点的坐标
vector<int> idx; // 存放点的原始横坐标
vector<int> idy; // 存放点的原始纵坐标
// 将横坐标离散化，映射到某个下标 用的二分查找
int findx(int x){
    int l = 0, r = idx.size() - 1;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(idx[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射下标从1开始，便于计算前缀和
}
// 将纵坐标离散化，映射到某个下标
int findy(int x){
    int l = 0, r = idy.size() - 1;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(idy[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

int main(){
    cin >> n >> m;
    // n个点
    for(int i = 0; i < n; i ++ ){
        int x, y;
        cin >> x >> y;
        point.push_back({x, y});
        idx.push_back(x);
        idy.push_back(y);
    }
    // 分别对横坐标、纵坐标排序、去重
    sort(idx.begin(), idx.end());
    idx.erase(unique(idx.begin(),idx.end()), idx.end());
    sort(idy.begin(), idy.end());
    idy.erase(unique(idy.begin(),idy.end()), idy.end());
    
    // 处理原始点，映射下标
    for(int i = 0; i < n; i ++ ){
        int x = findx(point[i][0]);
        int y = findy(point[i][1]);
        a[x][y] ++;
    }
    // 处理前缀和
    for(int i = 1; i <= idx.size(); i ++ )
       for(int j = 1; j <= idy.size(); j ++ ){
           s[i][j] = a[i][j] + s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1];
       }
    // 处理询问
    for(int i = 0; i < m; i ++ ){
        int x1, y1, x2, y2;
        int p, q;
        cin >> p >> q;
        x1 = point[p][0], y1 = point[p][1], x2 = point[q][0], y2 = point[q][1];
        x1 = findx(x1), y1 = findy(y1), x2 = findx(x2), y2 = findy(y2);
        cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
        
    }
    
    return 0;
}

时间复杂度

排序：$O(nlogn)$
处理原始点，映射下标：$O(nlogn)$

处理前缀和: $O(n^2)$
处理询问：$O(m)$

前缀和优化了询问，否则复杂度为$O(m\ast n^2)$
离散化优化了数组维度N，优化后的N与点的个数n相近（可略大更保险，保证数组运算不越界），否则N需要涵盖数的范围$[-2^{31},2^{31}-1]$， 即$2^{32}$，则$O(N^2)$将严重超时，难以计算。