一、平衡二叉树

110.平衡二叉树
依旧是使用后序遍历来统计高度。

递归过程中，发现某节点的左右子树的高度差超过了1，我们就直接返回-1，不返回节点的高度了。

递归函数的参数和返回值：

int getHeight(TreeNode * node){}

终止条件：

if(node==nullptr) return 0;

单层递归逻辑：

如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？
当然是其左子树高度和其右子树高度的差值。分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。

int leftHeight = getHeight(node->left);   // 左
if (leftHeight == -1)
    return -1;
int rightHeight = getHeight(node->right); // 右
if (rightHeight == -1)
    return -1;

int res;
if (abs(leftHeight - rightHeight) > 1)  // 根
    res = -1;
else
{
    res = 1 + max(leftHeight, rightHeight);
}
return res;

完整代码：

class Solution
{
public:
    int getHeight(TreeNode *node)
    {
        if (node == nullptr)
            return 0;

        int leftHeight = getHeight(node->left); // 左
        if (leftHeight == -1)
            return -1;
        int rightHeight = getHeight(node->right); // 右
        if (rightHeight == -1)
            return -1;

        int res;
        if (abs(leftHeight - rightHeight) > 1)  // 根
            res = -1;
        else
        {
            res = 1 + max(leftHeight, rightHeight);
        }
        return res;
    }
    bool isBalanced(TreeNode *root)
    {
        return getHeight(root) == -1 ? false : true;
    }
};

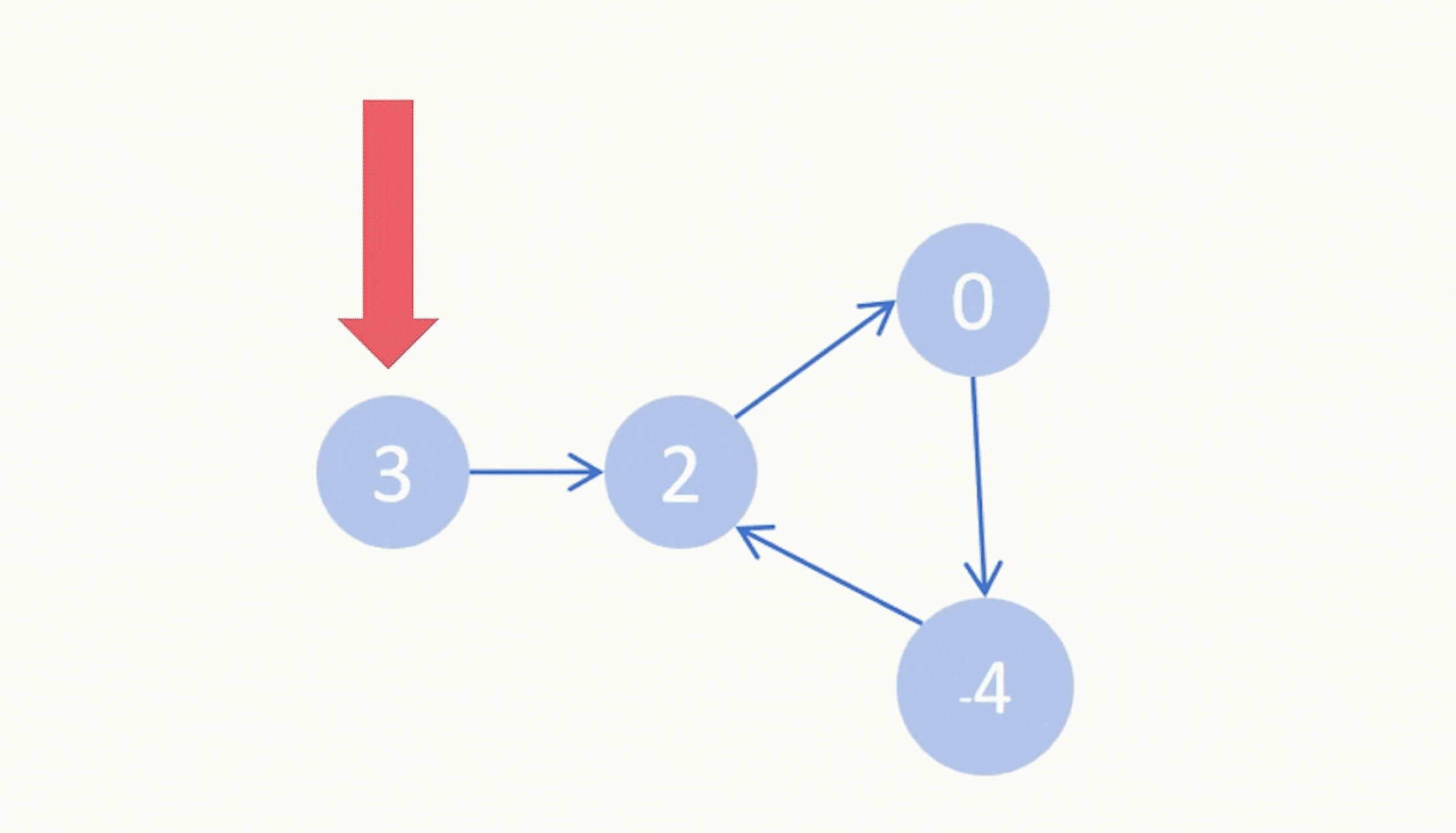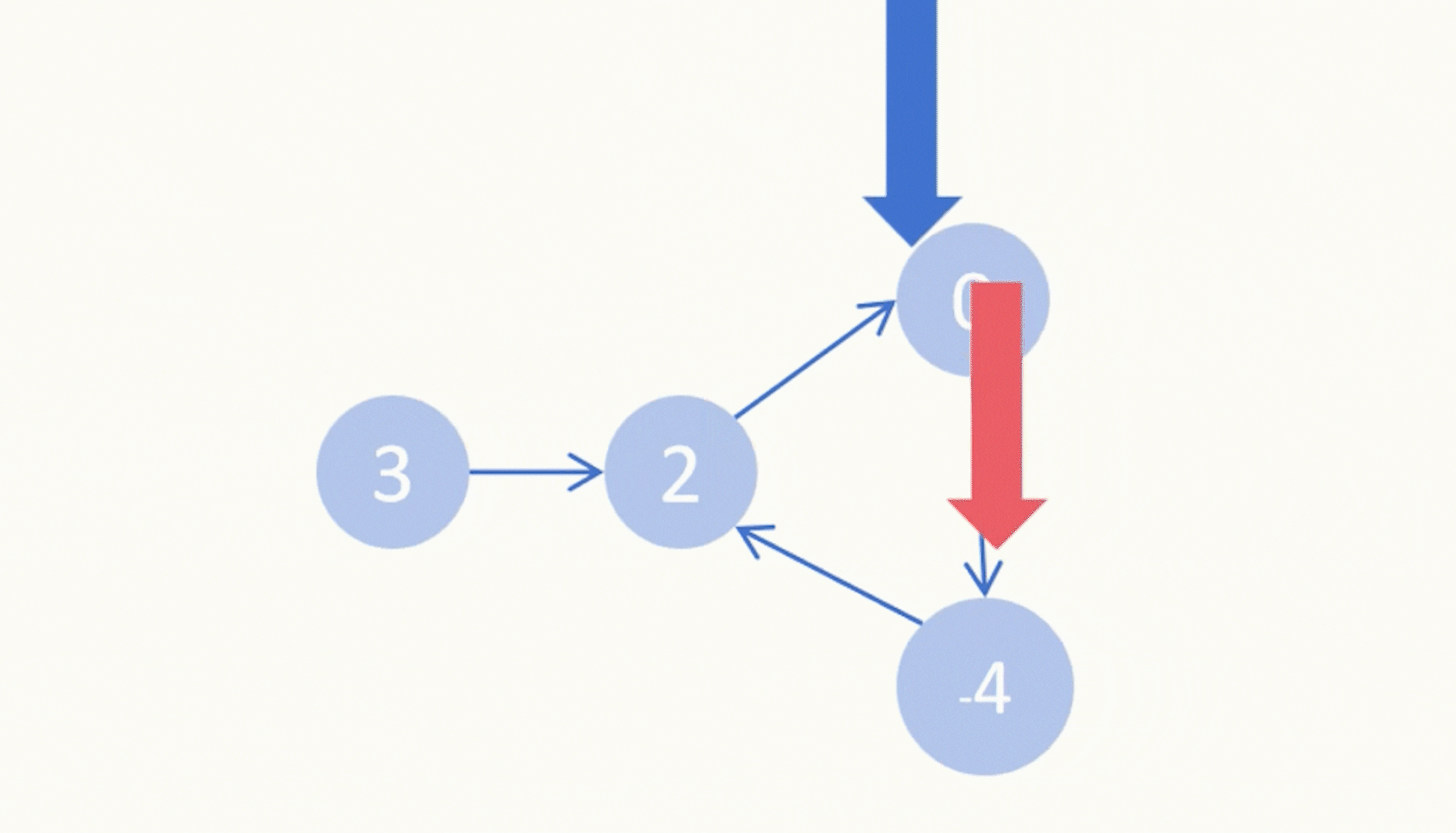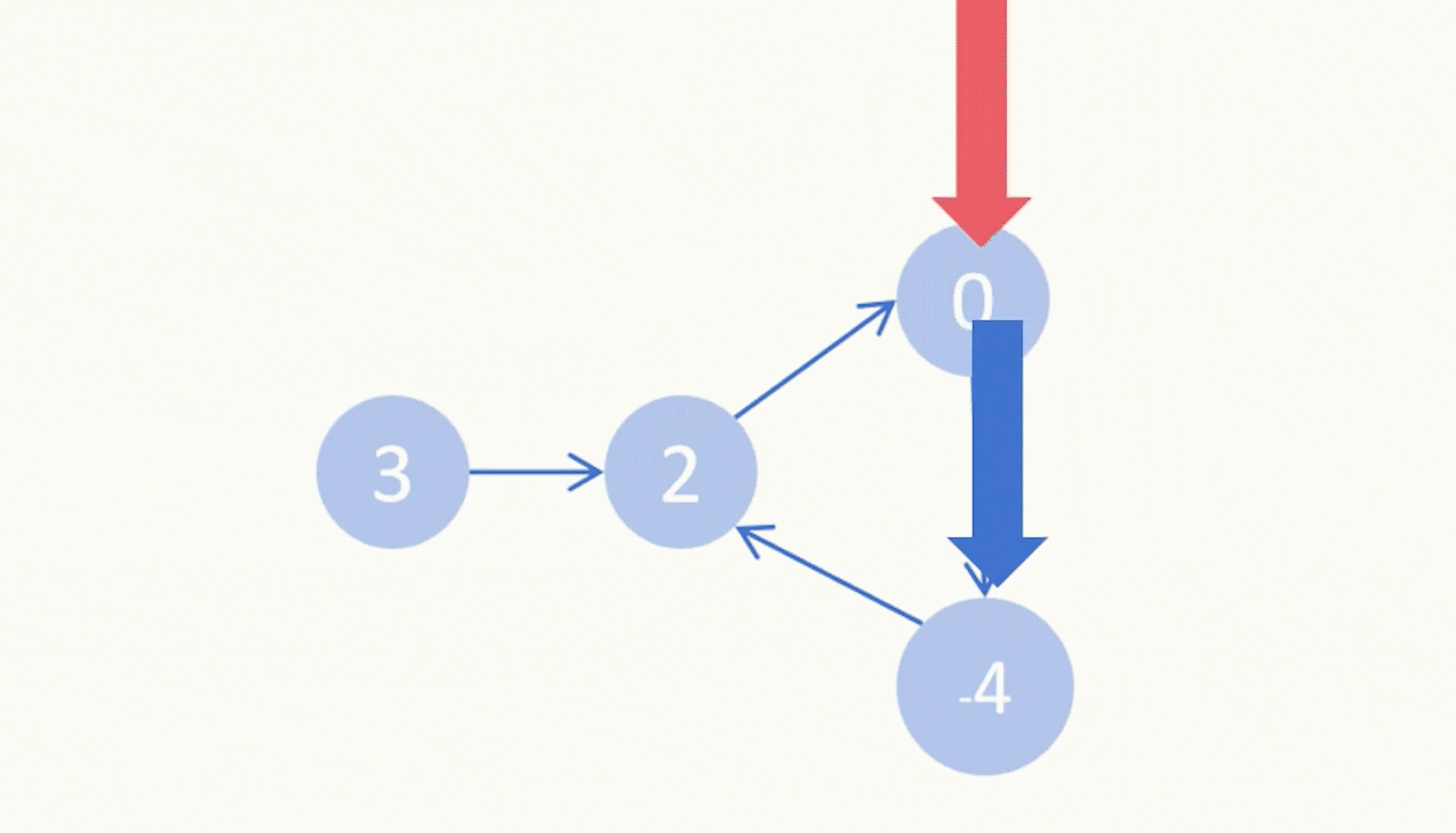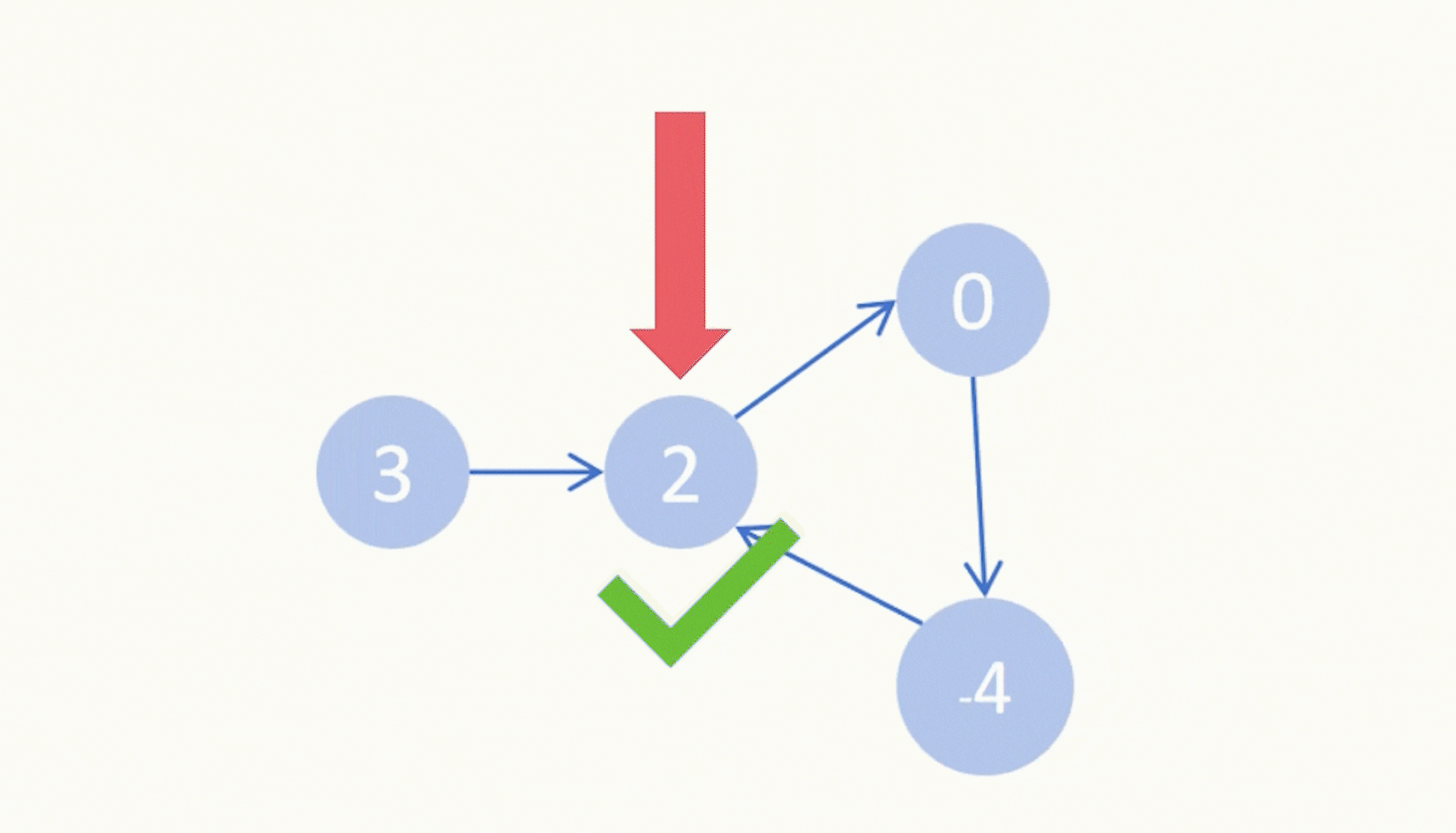
二、[回溯小难]二叉树的所有路径

257.二叉树的所有路径

我们这里要使用前序遍历。

递归函数的参数和返回值：

void travelsal(TreeNode *node){}

递归终止条件：

if (node->left == nullptr && node->right == nullptr)

单层递归逻辑：

// 单层递归处理逻辑
// 左
if (node->left)
{
    travelsal(node->left);
    path.pop_back(); // 为啥在这里pop_back()? 这是回溯的过程
}
// 右
if (node->right)
{
    travelsal(node->right);
    path.pop_back(); // 为啥在这里pop_back()? 这是回溯的过程
}

class Solution
{
private:
    vector<string> res;
    vector<int> path;
    void travelsal(TreeNode *node)
    {
        path.push_back(node->val); // 中 写在这里？ 因为最后一个叶子节点也要加入到path中
        if (node->left == nullptr && node->right == nullptr)
        {
            string s;
            for (int i = 0; i < path.size() - 1; i++)
            {
                s += to_string(path[i]);
                s += "->";
            }
            s += to_string(path[path.size() - 1]); // 记录最后一个节点(叶子节点)
            res.push_back(s);
            return;
        }
        // 中 本该写在这里
		//path.push_back(node->val);
        
        // 单层递归处理逻辑
        // 左
        if (node->left)
        {
            travelsal(node->left);
            path.pop_back(); // 为啥在这里pop_back()? 这是回溯的过程
        }
        // 右
        if (node->right)
        {
            travelsal(node->right);
            path.pop_back(); // 为啥在这里pop_back()? 这是回溯的过程
        }
    }

public:
    vector<string> binaryTreePaths(TreeNode *root)
    {
        travelsal(root);
        return res;
    }
};

1、为啥用前序？
这样才方便让父节点指向孩子节点，找到对应的路径。

2、为什么会有回溯？
因为我们要用vector装数据，然后要把数据弹出去一部分，方便递归其他路径。

三、左叶子之和

404.左叶子之和

使用后续遍历最为简洁。
判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

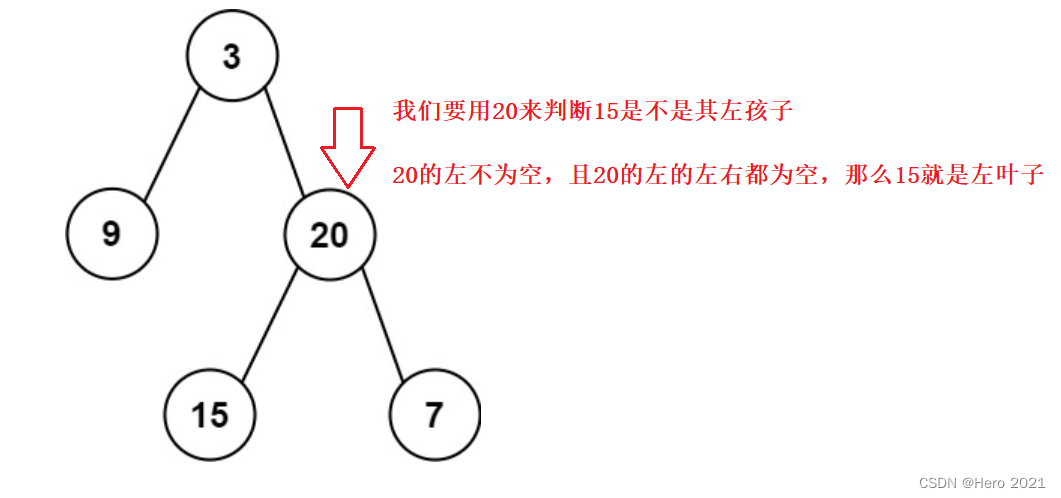
递归函数的参数和返回值：

int travelsal(TreeNode *node){}

终止条件：

 if (node == nullptr)
     return 0;

单层递归逻辑：

int leftnum = travelsal(node->left); // 左
if (node->left != nullptr && node->left->left == nullptr && node->left->right == nullptr)
    leftnum = node->left->val;
int rightnum = travelsal(node->right);// 右
int sum = leftnum + rightnum; // 中
return sum;

完整代码：

class Solution
{
public:
    int travelsal(TreeNode *node)
    {
        if (node == nullptr)
            return 0;

        int leftnum = travelsal(node->left);
        if (node->left != nullptr && node->left->left == nullptr && node->left->right == nullptr)
            leftnum = node->left->val;
        int rightnum = travelsal(node->right);
        int sum = leftnum + rightnum;
        return sum;
    }
    int sumOfLeftLeaves(TreeNode *root)
    {
        return travelsal(root);
    }
};