哈工大计算机网络课程网络安全基本原理详解之:消息完整性与数字签名
这一小节,我们继续介绍网络完全中的另一个重要内容,就是消息完整性,也为后面的数字签名打下基础。
报文完整性
首先来看一下什么是报文完整性。
报文完整性,也称为消息完整性(message integrity),有时也称为报文/消息认证(或报文鉴别),目标:
-
证明报文确实来自声称的发送方
比如接收端在收到报文时能够确认,报文是由指定发送方发送的。这一过程也是与我们上一节中介绍的身份认证相关的。
-
验证报文在传输过程中没有被篡改。
-
预防报文的时间、顺序被篡改。
-
预防报文持有期被修改。
比如Bob给Alice发报文,还应该预防Alice在持有报文时,有意或无意修改报文。
-
预防报文在发送/接收时对报文本身的抵赖
- 发送方否认。比如发送方否认发送过这个报文,或否认发送报文的内容。
- 接收方否认。比如接收方否认收到过这个报文,或否认接收报文的内容。
密码散列函数
在解决报文完整性的问题中,需要使用到一个非常重要的概念,就是密码散列函数。
密码散列函数(Cryptographic Hash Function):H(m)。
用H(m)来表示利用密码散列函数对报文m进行的散列运算。
作为密码散列函数,与我们一般性的散列函数,具有以下一些特征:
-
散列算法公开
-
H(m)能够快速计算
-
对任意长度报文进行多对一映射,均产生定长输出
-
对于任意报文无法预知其散列值
-
不同报文不能产生相同的散列值
-
单向性:无法根据散列值倒推出报文
- 即对于给定散列值h,无法计算找到满足h=H(m)的报文m
-
抗弱碰撞性(Weak Collision Resistence-WCR)
- 对于给定报文x,计算上不可能找到y且y不等于x,使用H(x) = H(y)
-
抗强碰撞性(Strong Collision Resistence-SCR)
- 在计算中,不可能找到任意两个不同报文x和y(x≠y),使得H(x) = H(y)。
密码散列函数对报文完整性的校验是至关重要的。
作为与一般性的散列函数的对比,我们来看一个例子。
在之前讲解IP协议中,会有一个16比特的checksum校验和来在接收端判断数据报是否有修改。在这种校验和的计算中,其实也具备散列函数的某些属性:
- 多对一映射
- 对于任意报文,产生固定长度的散列值(16-bit校验和)
但是它并不能作为密码散列函数,因为对于给定的报文及其散列值,很容易找到另一个具有相同散列值的不同报文。比如下面这个例子:

散列函数算法
通过上面的介绍可以看出,密码散列函数的要求是比较严格的,需要经过精心设计。目前,在网络安全领域,使用的比较常见的有以下两个函数:
- MD5:被广泛应用的散列函数(RFC 1321)
- 通过4个步骤,对任意长度的报文输入,计算输出128位的散列值。
- MD5不是足够安全。在1996年,Dobbertin找到了两个不同的512-bit块,在MD5计算下产生了相同的散列值。
- SHA-1(Secure Hash Algorithm)
- 另一个相对更安全的散列函数
- US标准
- SHA-1要求输入消息长度<264
- SHA-1的散列值为160位
- 速度慢于MD5,安全性优于MD5
报文摘要
报文摘要实际上是利用上面的密码散列函数,作用于某一任意长度的报文m,得到一个固定长度的散列值,通常把这个散列值称为报文摘要(message digest),记为H(m)。

这个报文摘要对原报文来说,是具有非常重要的意义的。重要的意义在于,报文摘要可以作为报文m的数字指纹(fingerprint)。
报文认证
有了上面的基础概念后,接下来我们就着重讨论下如何实现报文完整性的认证。
简单方案
简单方案:报文+报文摘要—>扩展报文(m, H(M))
上述简单方案利用了密码散列函数和报文摘要来实现。实际上,就是在给对方发送报文时,利用密码散列函数根据该报文内容,计算出一个报文摘要。此时,发送的报文内容除了其本身原有内容外,还包含一个报文摘要。两者构造出一个扩展报文,发送给对方。
接收方在收到该扩展报文后,根据同样的密码散列函数,根据报文内容计算得到一个散列值,然后跟报文摘要进行比对。如果一致,说明报文在传输过程中没有被修改,如果不一致,则说明已经被修改。
整体的大致过程如下所示:

为了在报文认证中,除了确保报文在传输过程中没有发生过改变外,还要认证报文的发送方确实是指定的真实发送方,而不是第三方入侵者或伪造的(身份认证),还需要对上述方案进行改进。
报文认证码MAC
报文认证码MAC:(Message Authentication Code)
实现原理:
- 引入了一个报文认证密码的概念
- 此时,一个扩展报文(m, H(m+s))包括了:原始报文m + 认证密钥s + 密码散列函数H
在使用这种方案下,报文认证过程大致如下所示:
- 发送端在发送报文中,利用密码散列函数H,对原始报文内容m和认证密码s(一般就是一个字符串或比特串)一起共同生成一个报文摘要H(m+s)。
- 该报文摘要与原始报文一起构成一个扩展报文(m ,H(m,s))
- 接收端收到该报文后,分离出原始报文和报文摘要两部分。
- 对于原始报文,利用相同的密码散列函数和认证密钥s,得到一个散列值H(m,s)
- 同样的,将该散列值与报文摘要的值比对,如果匹配,则报文完整性成功认证。否则,认证失败。

这里为什么就能够确认报文是来自指定的真实发送方,而不是伪造或第三方入侵者呢?因为,这里引入了密钥的概念,而这对密钥只有发送方和接收方所持有。由于密码散列函数的特殊性,只有该密钥才能生成相应的报文摘要,从而保证了报文认证的可靠性。
报文验证码MAC在一定程度上解决了报文完整性校验和身份认证问题,但是报文完整性里涉及的其他问题,还很难解决。比如,接收端在持有报文时,由于它有密码s,因此,它可以任意构造一个报文内容m’,并利用该密钥s生成相应的报文摘要,然后伪造说这是发送方发送的报文。这里的问题,就涉及到我们开篇报文完整性要求中说的,预防报文持有期被修改和预防抵赖。
为了解决这些问题,就需要引入我们接下来介绍的数字签名概念。
数字签名
上面我们最后说到,作为报文验证码MAC实际上有一些其他的报文完整性问题还未解决。比如,涉及到下面这些问题。
Q:如何解决下列与报文完整性相关的问题?
- 否认:发送方不承认自己发送过某一报文。
- 伪造:接收方自己伪造一份报文,并声称来自发送方
- 冒充:某个用户冒充另一个用户接收后发送报文
- 篡改:接收方对收到的信息进行篡改。
这些问题,简单依赖单一的报文认证码是很难解决的。目前比较有效的,也是在网络安全中使用比较广泛的解决方案,就是数字签名(Digital signatures)。
- 数字签名技术是实现安全电子交易的核心技术之一。
- 可验证性(verifiable),验证报文是否被修改过。
- 不可伪造性(unforgeable)
- 不可抵赖性(non-repudiation)
数字签名的简单实现原理
显然我们很容易想到,**签名的主要目的是为了预防修改,即签名本身是不能被修改的,被签名的内容是不能被修改的。**就跟我们日常生活中,对一个文件的签名,往往就是签上自己的姓名,甚至手印,而且要保存原件,就是为了签名后,签名和文件内容都是不能被修改的。
因此,与日常生活中的签名行为联系起来的话,网络安全中的数字签名技术,实际上就是在发送的报文(相当于文件),签上一个数字名称,这个名称保证了报文的完整性,同时也标识着身份认证。同时,这个签名一定是唯一特殊,不可被修改的,从而保证不可伪造和不可抵赖性。
因此,为了实现数字签名,就需要借助于上面介绍的加密技术。报文加密技术是数字签名的基础。
同时,对于加密技术,首先不能选取对称加密算法,因为对称加密算法接收和发送双方使用的是同一个密钥,也就是说接收方是可以利用这个密码对接收报文进行修改的,也就是我们上面说的报文验证码的问题。
因此,对于加密算法的算法一定需要选择非对称加密算法(公钥技术)。此时,假设Bob要想Alice发送带有数字签名的信息,就可以利用其私钥对报文m进行加密,创建签名报文,KB-(m)。
整体流程如下所示:

作为Alice,实际上接收了两份报文:一份是明文原始报文m,另一份是Bob用私钥加密的签名报文。之后,Alice的响应帧流程大致如下所示:
-
Alice利用Bob的公钥KB+解密KB-(m),并检验KB+(KB-(m))= m来证实报文m确实是由Bob签名的。
-
如果KB+(KB-(m))= m成立,则签名m的一定是Bob的私钥
-
于是:
Alice可以证实:
- Bob签名了m
- 没有其他人签名m的可能
- Bob签名的是报文m而不是其他报文m‘
不可抵赖:
- Alice可以持有报文m和签名KB-(m),必要是可以提交给法院证明是Bob签名的报文m。
实际上,通过上面的介绍我们细想就能发现,实际上报文验证码MAC和数字签名技术的实现区分,实际上也就是对称加密算法和非对称加密算法实现原理的区别。因为有了非对称加密算法,使得每个用户都可以保留自己的私钥,同时公开一个公钥来进行解密。而这个私钥就成了身份认证的唯一标识,比如身份证ID,或指纹。从而保证了报文传输过程中的消息完整性和身份认证。
签名报文摘要
上述简单数字签名的方案有一个较大的缺点,就是在利用私钥对报文加密后(签名后),该签名要跟着报文一起发送给接收端。一来,传输的报文量相当于是两倍的报文,造成信道资源消耗。二来,接收方在对签名解密时,原始报文往往比较大,解密速度也会比较慢。因此,可以设计一些方案来改进这个签名过程。
怎么做呢?可以联想到上面提到过的报文摘要,对于报文摘要来说,它可以作为报文的数字指纹这样一个特征,也就是可以唯一标识一个报文。换句话说,报文摘要其实就与原始报文一一对应。
因此,显而易见,我们在签名的时候可以不对整个原始报文进行签名,而改为对这个报文摘要进行签名,也可以实现同样的效果。
因此,目前大部分的数字签名,使用的都是报文摘要签名的方法。
接下来我们来看一下,利用报文摘要数字签名的实现流程:
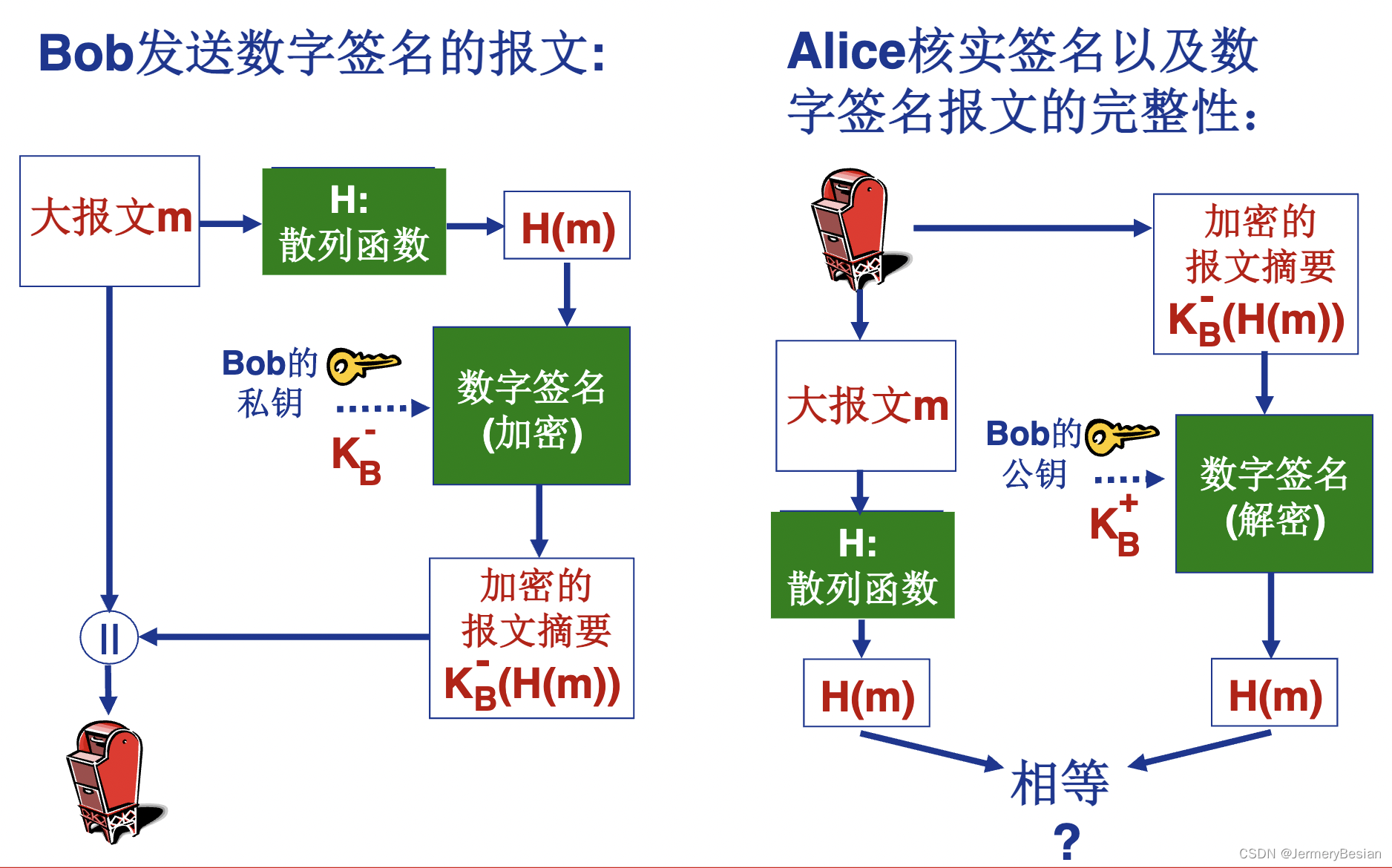
Bob发送数字签名的报文:
- Bob在发送报文时,利用密码散列函数,对报文生成报文摘要H(m)
- Bob利用自己的私钥,对报文摘要进行签名,得到签名后的报文摘要:KB-(H(m))
- 把该签名后的报文摘要和报文一起,组成扩展报文(m, KB-(H(m)))发送给接收端。
Alice核实签名以及数字签名报文的完整性:
- Alice分离出原始报文本身,和签名报文摘要
- Alice利用相同的密码散列函数,根据原始报文,生成报文摘要
- 再利用Bob的公钥对签名报文摘要进行解密
- 将解密后的报文摘要与刚刚生成的报文摘要进行比对,判断两者是否相同。