基于应用值迭代的马尔可夫决策过程(MDP)的策略的机器人研究（Matlab代码实现）

news2024/9/28 5:33:38

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

MDP（Markov Decision Process）是一种用于建模决策问题的数学框架，而机器人网格是一种常见的环境模型，用于描述机器人在离散的网格世界中移动和执行动作的问题。

在机器人网格中，通常将环境表示为一个二维网格，每个网格单元可以是机器人可以到达的位置。机器人可以根据当前所处的网格位置和执行的动作来决定下一步的移动方向。常见的动作包括向上、向下、向左、向右等。

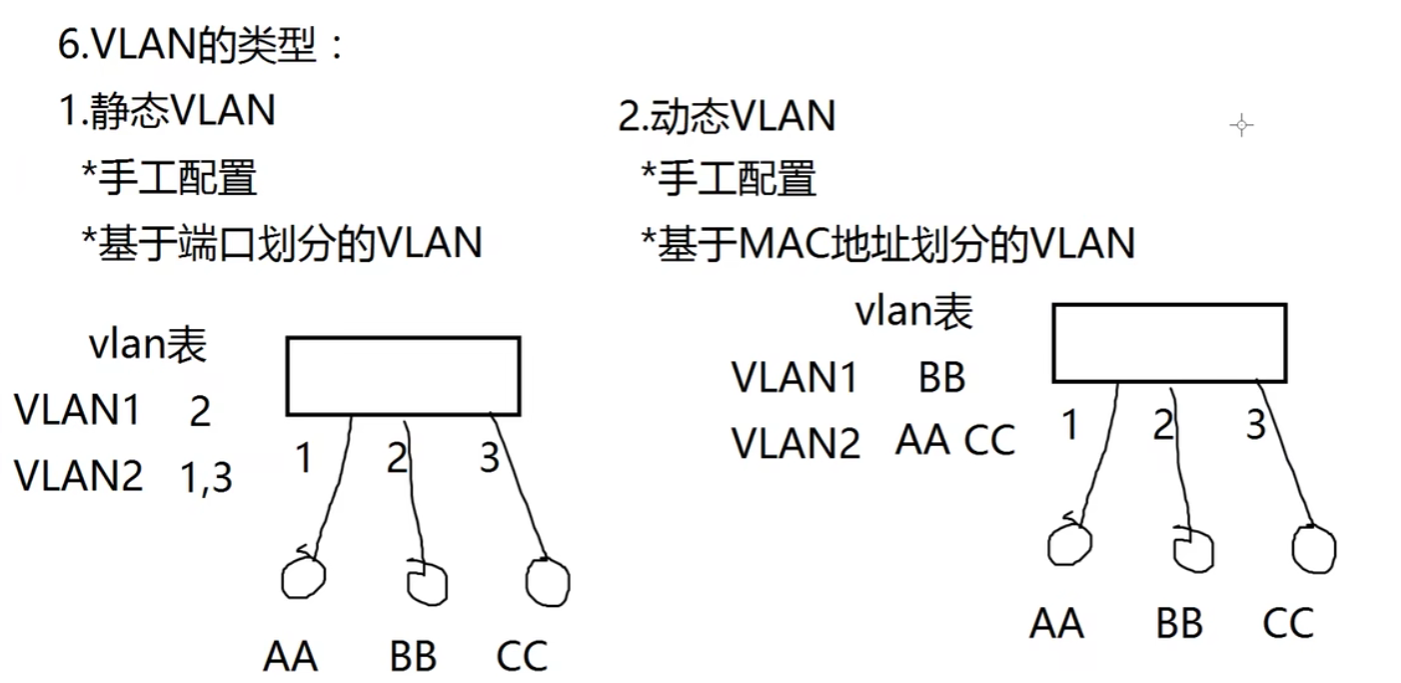
MDP可以用来描述机器人在网格世界中的决策问题。具体来说，MDP包括以下要素：
1. 状态（State）：在机器人网格中，状态可以表示机器人所处的网格位置。
2. 动作（Action）：机器人可以执行的动作，如向上、向下、向左、向右等。
3. 转移概率（Transition Probability）：给定当前状态和执行的动作，机器人转移到下一个状态的概率。
4. 奖励（Reward）：在每个状态执行每个动作时，机器人可以获得的奖励。
5. 值函数（Value Function）：用于评估每个状态的价值，表示从该状态开始，机器人能够获得的期望累积奖励。
6. 策略（Policy）：决定机器人在每个状态下选择哪个动作的策略。
通过建立MDP模型，可以使用强化学习算法（如值迭代、策略迭代、Q-learning等）来求解最优策略，使机器人在网格世界中能够做出最优的决策。

应用值迭代来学习马尔可夫决策过程（MDP）的策略 -- 网格世界中的机器人。
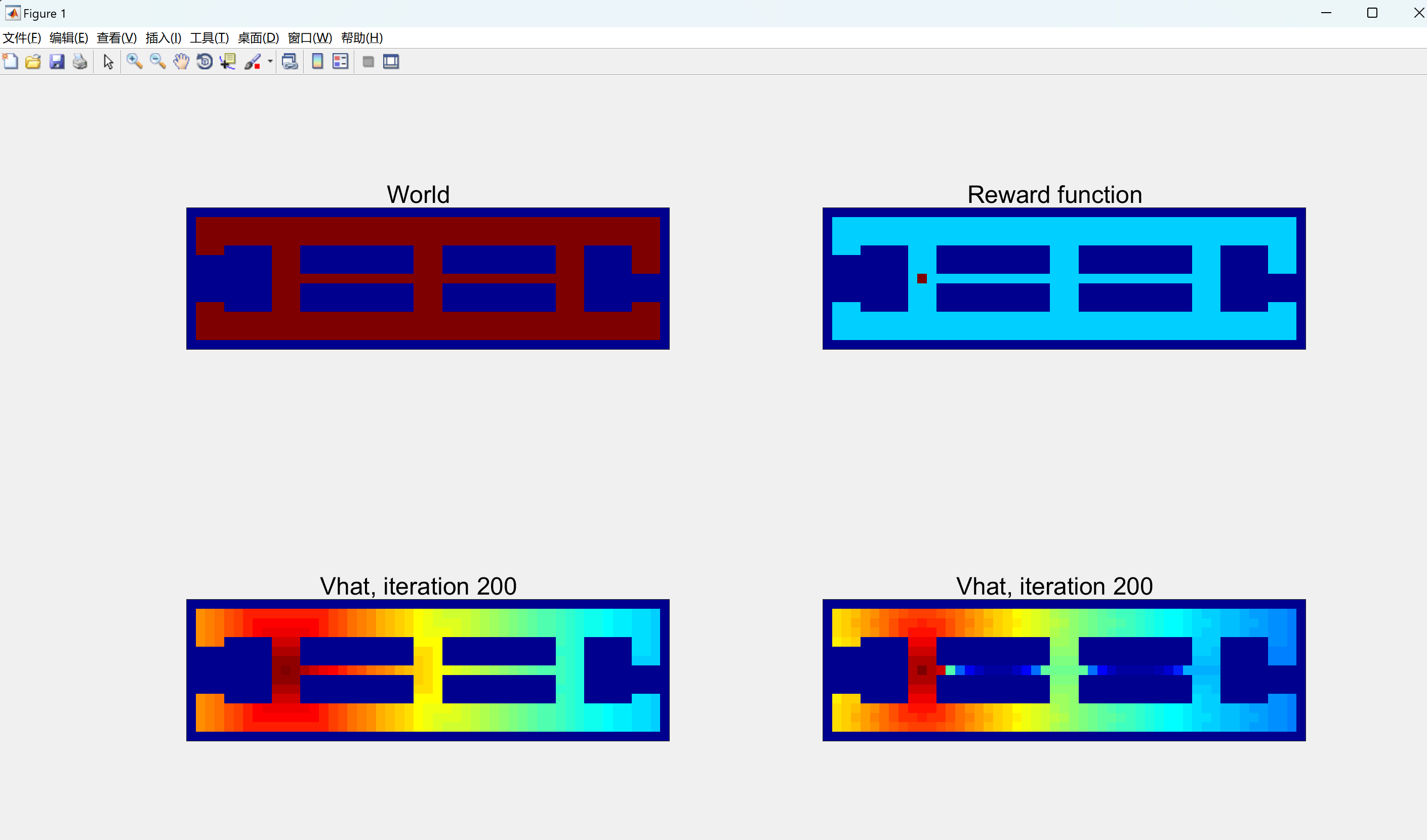
世界是自由空间（0）或障碍物（1）。每转一圈，机器人可以向8个方向移动，或保持在原地。奖励函数为一个自由空间，即目标位置提供高奖励。所有其他自由空间都有很小的惩罚，障碍物有很大的负奖励。值迭代用于学习最佳“策略”，该函数将
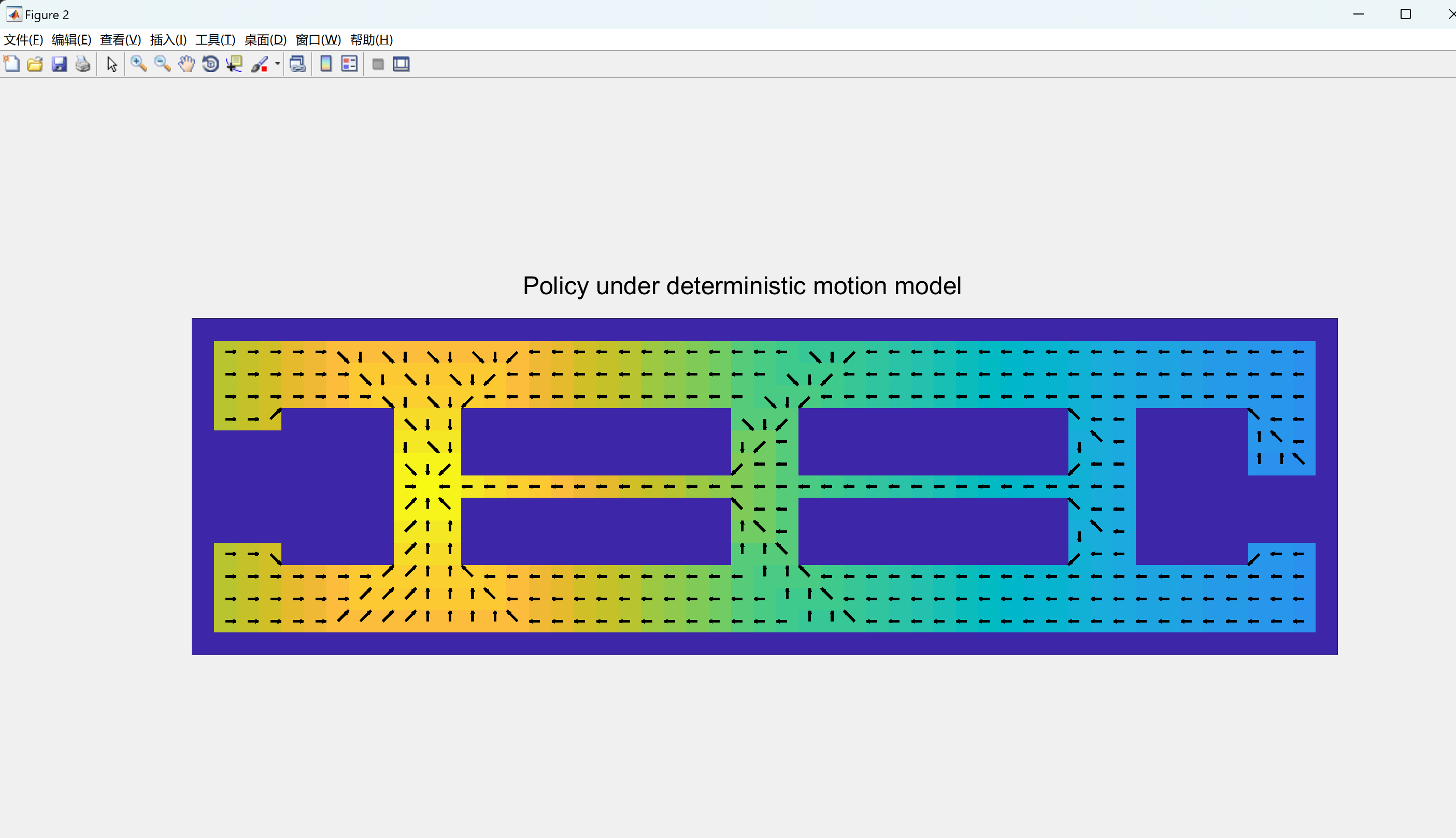
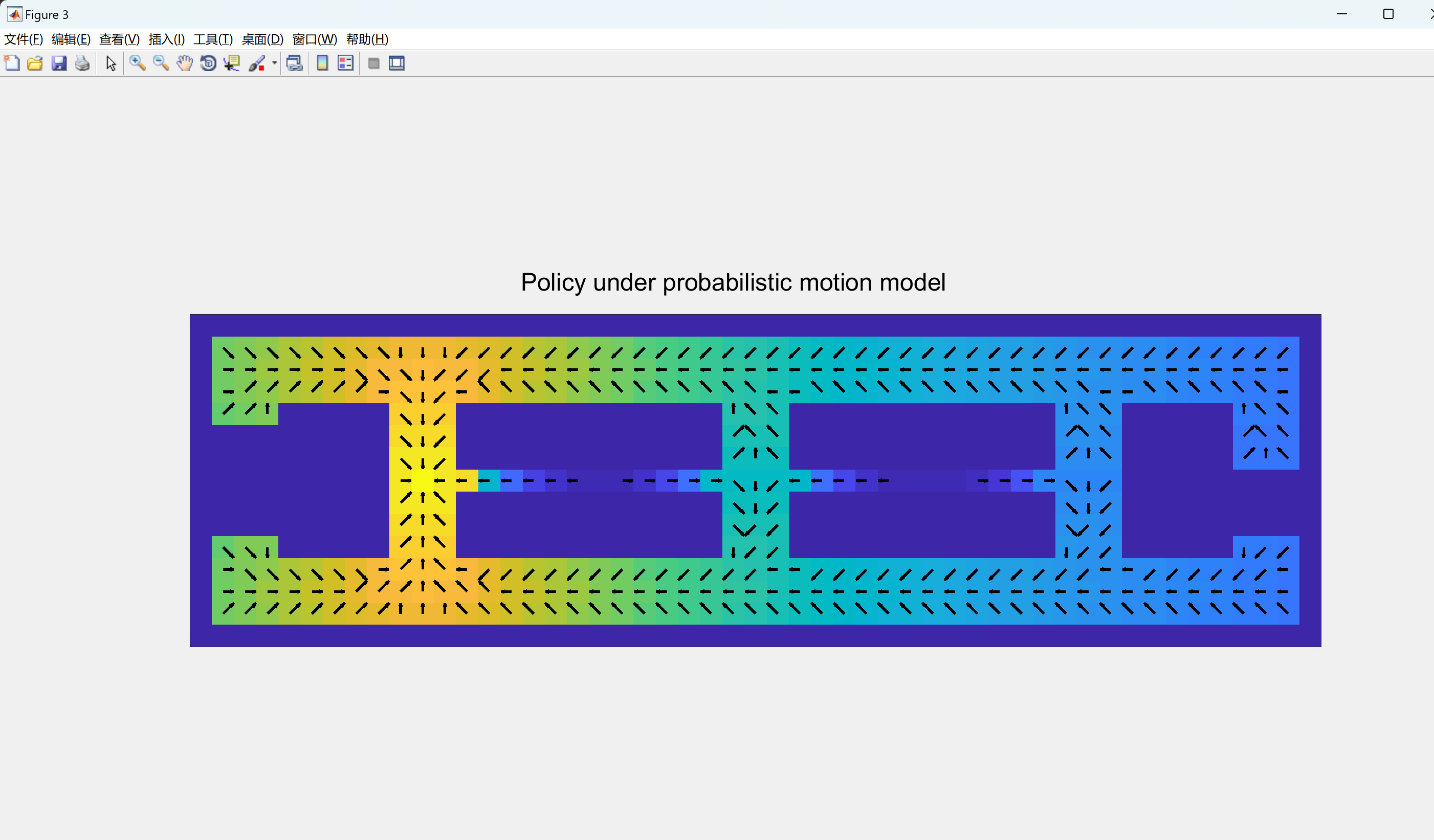
控制输入分配给每个可能的位置。本文将始终完美执行运动的确定性机器人与随机机器人进行比较，后者与命令移动的概率很小+/-45度。随机机器人的最佳策略是避开狭窄的通道并尝试移动到走廊的中心。

📚2 运行结果

部分代码：

% DRAW THE WORLD, REWARD, ANIMATE VALUE ITERATION, DISPLAY POLICY
subplot(2,2,1)
imagesc(~World);
set(gca,'Xtick',[], 'Ytick',[])
axis equal
axis tight
text(25,-1,'World','HorizontalAlignment','center','FontSize',18)
drawnow
if pauseOn; pause(); end %#ok<*UNRCH>

subplot(2,2,2)
imagesc(R);
axis equal
axis tight
set(gca, 'Xtick',[], 'Ytick',[])
text(25,-1,'Reward function','HorizontalAlignment','center','FontSize',18)
drawnow
if pauseOn; pause(); end

V_hat = MDP_discrete_value_iteration(R,World,false);
if pauseOn; pause(); end

DrawPolicy(V_hat,World,false);
if pauseOn; pause(); end

figure(f1)
V_hat_prob = MDP_discrete_value_iteration(R,World,true);
if pauseOn; pause(); end

DrawPolicy(V_hat_prob,World,true);
if pauseOn; pause(); end