参考代码：None

介绍

深度估计任务作为基础环境感知任务，在基础上构建的3D感知才能更加准确，并且泛化能力更强。单目的自监督深度估计已经有MonoDepth、ManyDepth这些经典深度估计模型了，而这篇文章是对多目自监督深度估计进行探索，在单目自监督深度估计基础上利用多目相机之间相互约束构建了多目自监督深度估计方法。具体为，在该方法中每个相机会预测自身深度图和位姿信息，依靠相机之间视角重叠关系、自身运动位姿、深度估计结果构建自监督损失，多目视角的使用主要用于约束各个视角下生成的位姿，而且正是由于使用了外参数使得网络具备了真实距离的感知能力。

方法设计

使用spatial-temporal的自监督深度估计

在单目深度估计任务中依靠不同时序下的成像结果构建广度重构误差，其典型形式为：
$$L_p(I_t,{\hat{I}}_t)=\alpha \frac{1-SSIM(I_t,{\hat{I}}_t)}{2}+(1-\alpha )||I_t-{\hat{I}}_t||$$
其中，${\hat{I}}_t$是通过估计出来的位姿和深度估计warp之后得到的，其warp的过程记为：
$${\hat{p}}^t=\pi ({\hat{R}}^{t\to c}\varphi (p^t,{\hat{d}}^t,K)+{\hat{t}}^{t\to c},K)$$
而在多目系统下除了能够像单目系统那样使用时序信息之外，还可以将空间信息引入（因为多目系统的相邻两个相机之间多存在重叠视角），或者将空间和时序信息混合使用（也就是当前帧经过时序warp之后在进行空间warp）。在下图中展示了多目系统在不同时序和空间维度下的变换关系。

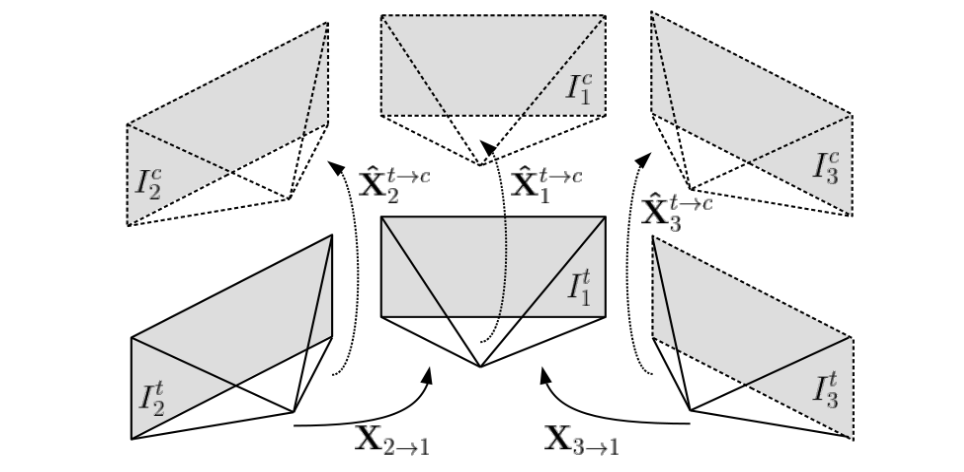
对于同时刻下可以依据相邻相机之前的内外参数将相机$i$的图像映射到相机$j$中去，也就是如下变换关系：
$${\hat{p}}_i={\pi }_j(R_{i\to j}{\varphi }_i(p_i,{\hat{d}}_i)+t_{i\to j})$$
在不同时刻下可以通过估计出来的位姿投影到相同时刻下，则在该相同时刻下可以构建temporal-spatial关联：
$${\hat{p}}_i^t={\pi }_j(R_{i\to j}({\hat{R}}_j^{t\to c}\varphi (p_j^t,{\hat{d}}_j^t)+t_j^{t\to c})+t_{i\to j})$$
使用这样关联关系可以使得重叠区域产生更多的响应像素，见下图（最后一行为temporal-spatial方式得到的响应区域）：

多目相机之间的位姿约束

由于算法中多目相机是各自单独预测位姿的，那么但是这些相机确是同处于一个运动系统中的，它们预先标定好的外参变换关系还是可以构建它们的约束关系的。则对于相邻的两个相机它们时序和空间上的对应约束为：
$${\bar{X}}_i^{t\to t+1}=X_j^{-1}{X}_i{\hat{X}}_i^{t\to t+1}{X}_i^{-1}{X}_j$$
上面的公式建立了不同相机在时序和空间上的变换关系，不过需要注意的是上面的公式是存在问题的。它的原理应该是依据周围相机各自预测出来的位姿，通过标定好的外参将预测出来的位姿变换到目的相机下，这样约束目的相机本身位姿估计结果和变换位姿，也就是从平移和旋转两个分量上使得两者近似：
$$t_{loss}=\sum _{j=2}^N||{\hat{t}}_1^{t+1}-{\bar{t}}_j^{t+1}|{|}^2$$
旋转分量上（旋转角）：
$$R_{loss}=\sum _{j=2}^N||{\hat{\varphi }}_1-{\bar{\varphi }}_1|{|}^2+||{\hat{\theta }}_1-{\bar{\theta }}_1|{|}^2+||{\hat{\Phi }}_1-{\bar{\Phi }}_1|{|}^2$$

损失计算的mask

在损失计算时采用两种类型的mask：non-overlaping和self-occlusion。对于第一种mask是根据重构误差的有效区域确定的，则会在temporal（相同相机不同时序）和spatial（不同相机相同时序）下在mask的引导下得到广度重构误差。

对于第二种那就由于设备本身安放位置决定得了，在计算过程中排除那些自身部分，其效果见下图：

实验结果

KITTI数据集：

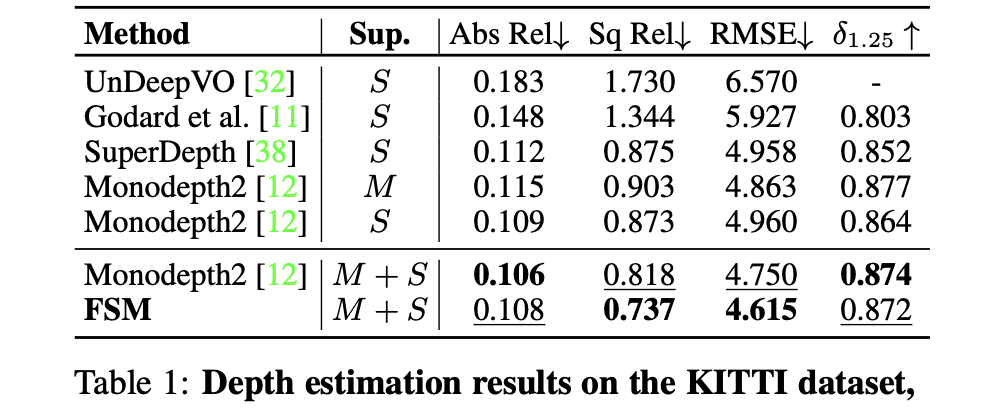
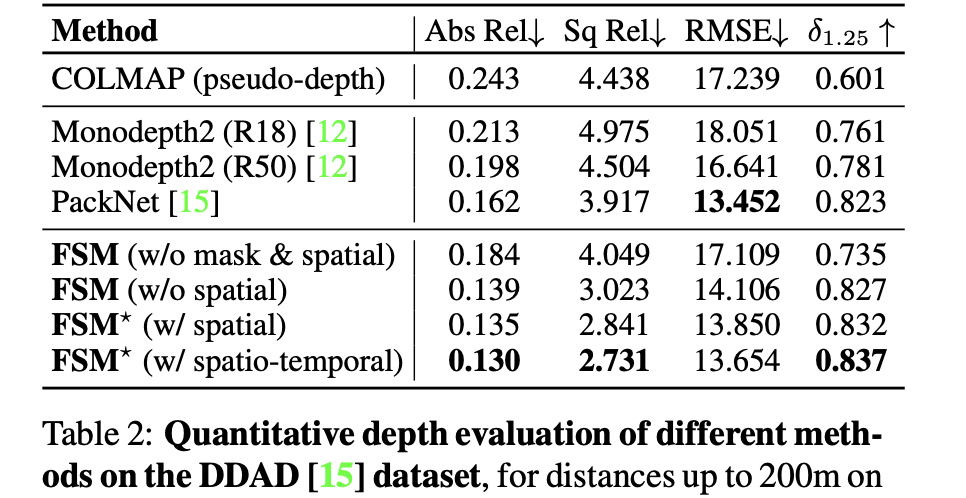
DDAD数据集：