代码实现
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
def forward(x):
return x * w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
print("w=", w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t', x_val, y_val, y_pred_val, loss_val)
print('MSE=', l_sum / 3)
w_list.append(w)
mse_list.append(l_sum / 3)
if __name__ == "__main__":
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
实验分析
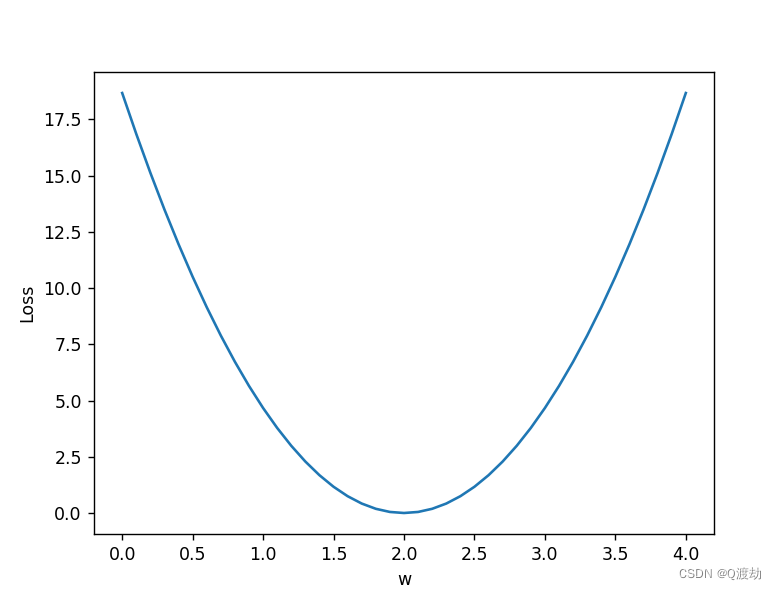
由上面实验结果可以看出,当 w = 2 时,损失函数降到最低。因此这个时候找到了最优的线性模
型即为 y^ = 2x