程序员自由创业周记#4：从一笔30美元的收入谈起

本文是一位程序员进行独立开发创业的记录，将分享创业过程中的所思所想以及收支明细。在文末，您还可以找到之前的历史文章。

惊喜之旅

这次的惊喜源于 学伟扫描Pro 在美国销售的第一笔订单，这标志着我的产品获得了漂亮国用户的认可，让我感到非常欣慰。学伟扫描 是我四年前尝试独立开发的第一款产品，最初命名为微扫描，但商标注册失败；后来改成了微扫，商标依然未能注册成功；最终，我决定将”学伟“注册为第9类软件商标，成功注册，于是有了这个朴实无华的名字。然而，无论名字如何，最重要的是产品本身。学伟扫描 上线三年来，在没有任何推广的前提下，收获了2.2万次下载，获得32个评分，其中30个是五星评价，1个是四星评价，1个是三星评价；好评率高达93.75%。因此，她确实挺好用，能够吸引漂亮国用户也就不足为奇了。值得一提的是，Pro版本在美区售价为30美元，而普通版本则为3.99美元（包年订阅）。

学伟扫描 的功能简介

简单来说，学伟扫描 的功能就是将照片中的文字提取出来，这项技术被称为OCR。除此之外，它还扩展了其他功能，比如：

• 当朋友发来一张充满文字的图片时，可以用它提取文字内容；
• 上课时拍摄了很多课件，可以用它按科目进行整理，并删除相册中的重复照片；
• 在刷微博时看到一张英文图片，不知道其意思，可以用它进行识别和翻译，从而了解其含义；
• 将一张或多张图片转换成PDF格式导出，或通过打印机进行打印。

突出优势

市面上类似的软件成百上千，甚至iPhone自带的拍照功能也具备OCR功能，那么学伟扫描 有何优势呢？

• 它采用了市面上最准确的API，确保了最高的识别准确率；
• 完全无广告，用户体验更加纯粹；
• 仅需0.25秒即可启动，操作更加高效便捷；
• 可以根据需要建立文件夹分类整理文件；
• 数据安全，所有资料均在本地管理，保障用户隐私。

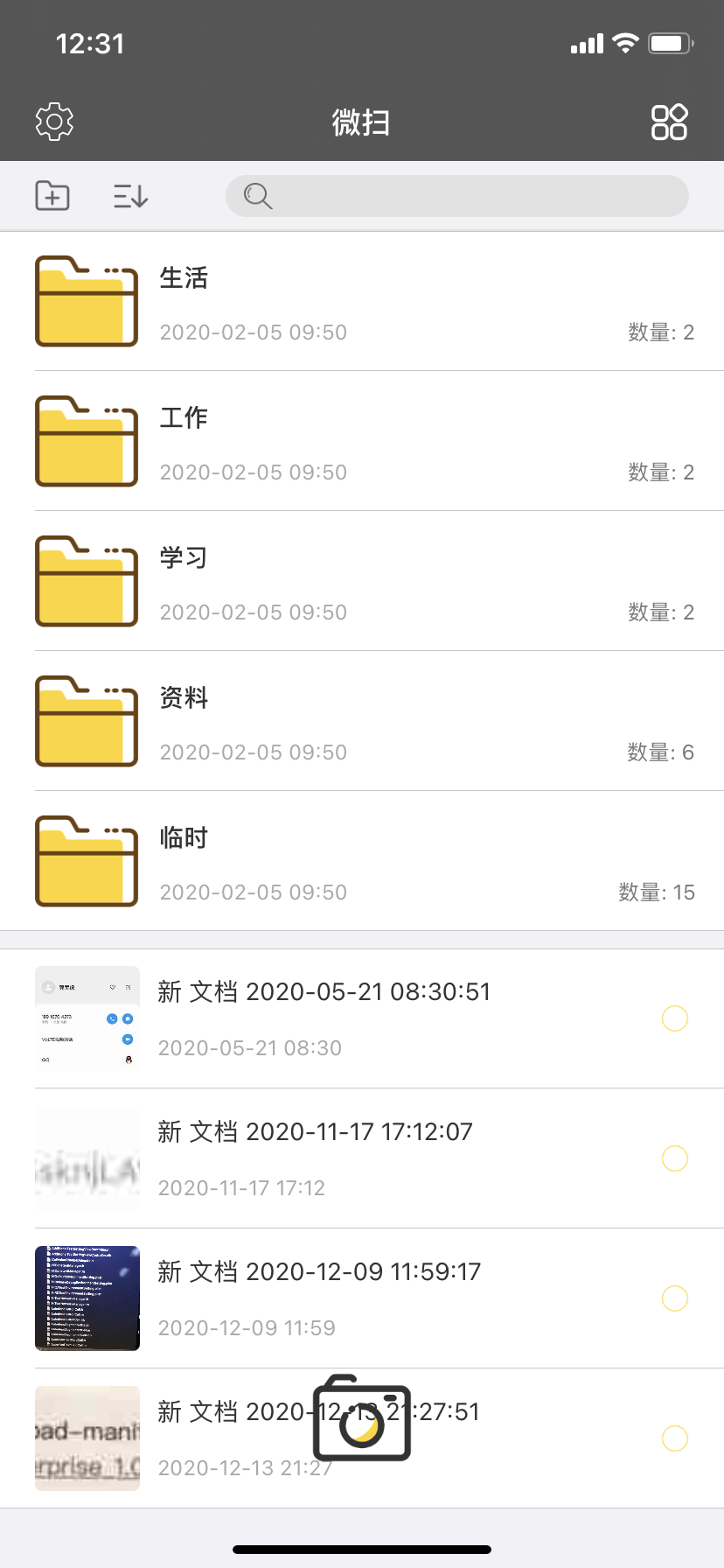
种下的种子

虽然 学伟扫描 三年来的收入还不足以覆盖一年开发者账号的年费，但它确实是当初我准备追求全职独立开发道路时所种下的一颗种子。通过这一过程，我深刻体验到开发一款完全属于自己的软件带来的乐趣。相比之下，为他人打工无论有多轻松都让我感到痛苦，而做自己的产品无论再累也让我感到幸福。

周更和往期文章

我的周记主要发布在个人博客：极客学伟 和 同名微信公众号上，期待您的关注。

往期文章：

• 程序员自由创业周记#1：做一场梦吧
• 程序员自由创业周记#2：前期准备
• 程序员自由创业周记#3：No1.作品