今天接到一个任务就是需要基于给定的数据集来进行数据挖掘分析相关的计算,并完成对未来时段内数据的预测建模,话不多少直接看内容。
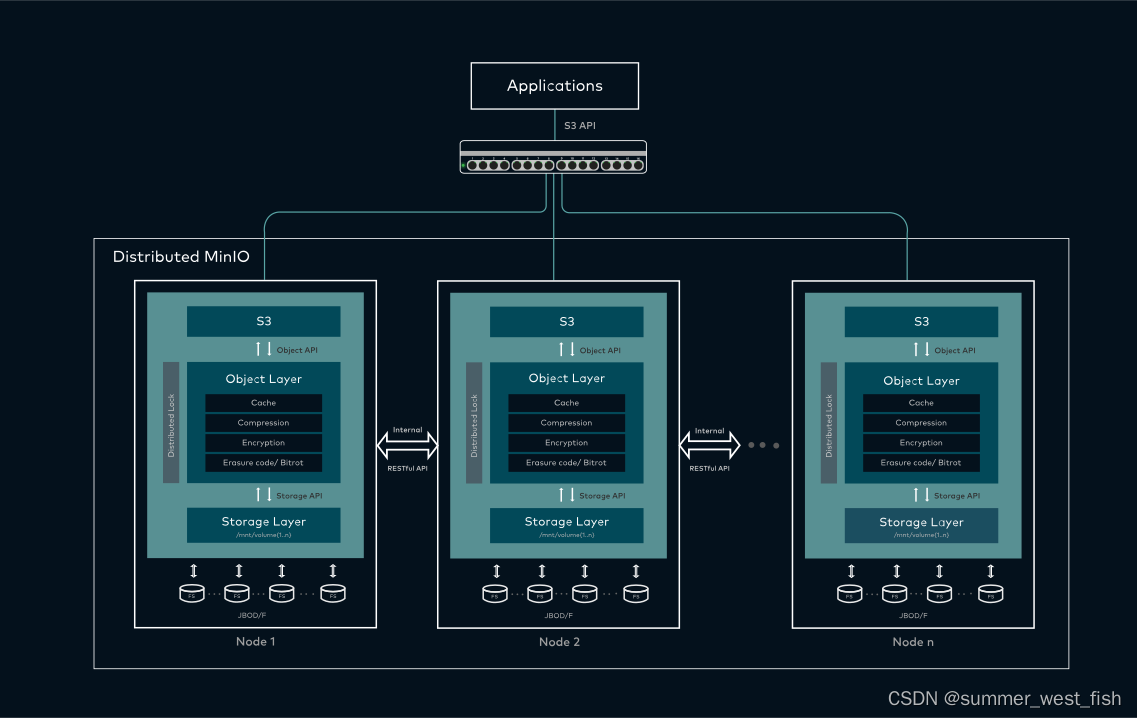
官方数据详情介绍在这里,如下所示:
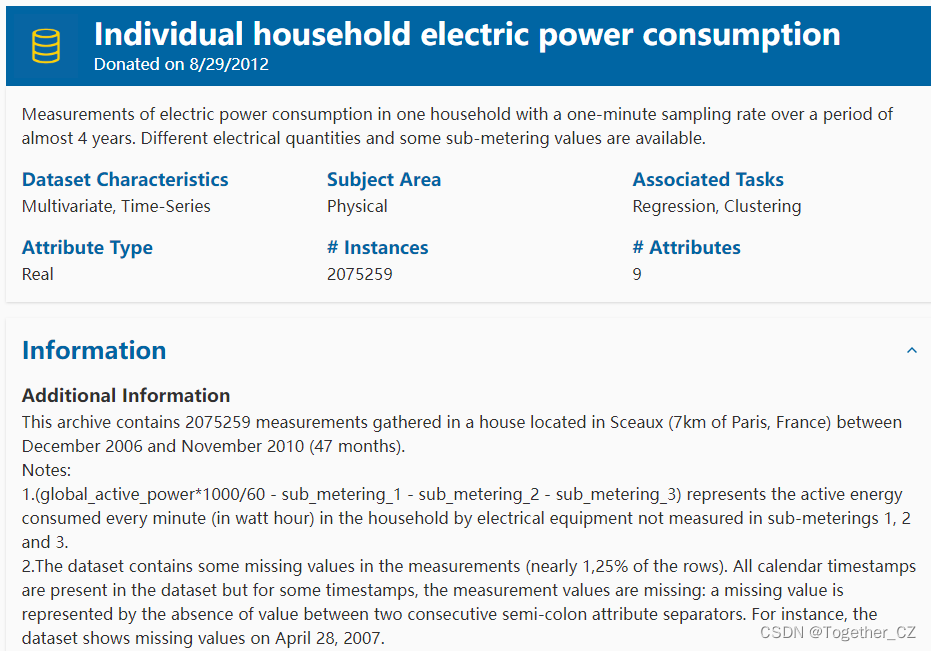
数据集中一共包含9个不同的字段,详情如下:
1.date:日期格式为dd/mm/yyyy
2.时间:时间,格式为hh:mm:ss
3.global_active_power:家庭全球分钟平均有功功率(千瓦)
4.global_reactive_power:家庭全球分钟平均无功功率(千瓦)
5.电压:分钟平均电压(单位:伏特)
6.global_intensity:家用全球分钟平均电流强度(安培)
7.sub_metering_1:1号能量子计量(以有功能量的瓦时为单位)。它对应于厨房,主要包括洗碗机、烤箱和微波炉(热板不是电动的,而是燃气的)。
8sub_metering_2:2号能量子计量(以有功能量的瓦时为单位)。它对应于洗衣房,里面有一台洗衣机、一台滚筒式干燥机、一台冰箱和一盏灯。
9_metering_3:3号能量子计量(以有功能量的瓦时为单位)。它对应于电热水器和空调。需要数据集的话可以自行下载,在这里。数据详情截图如下所示:
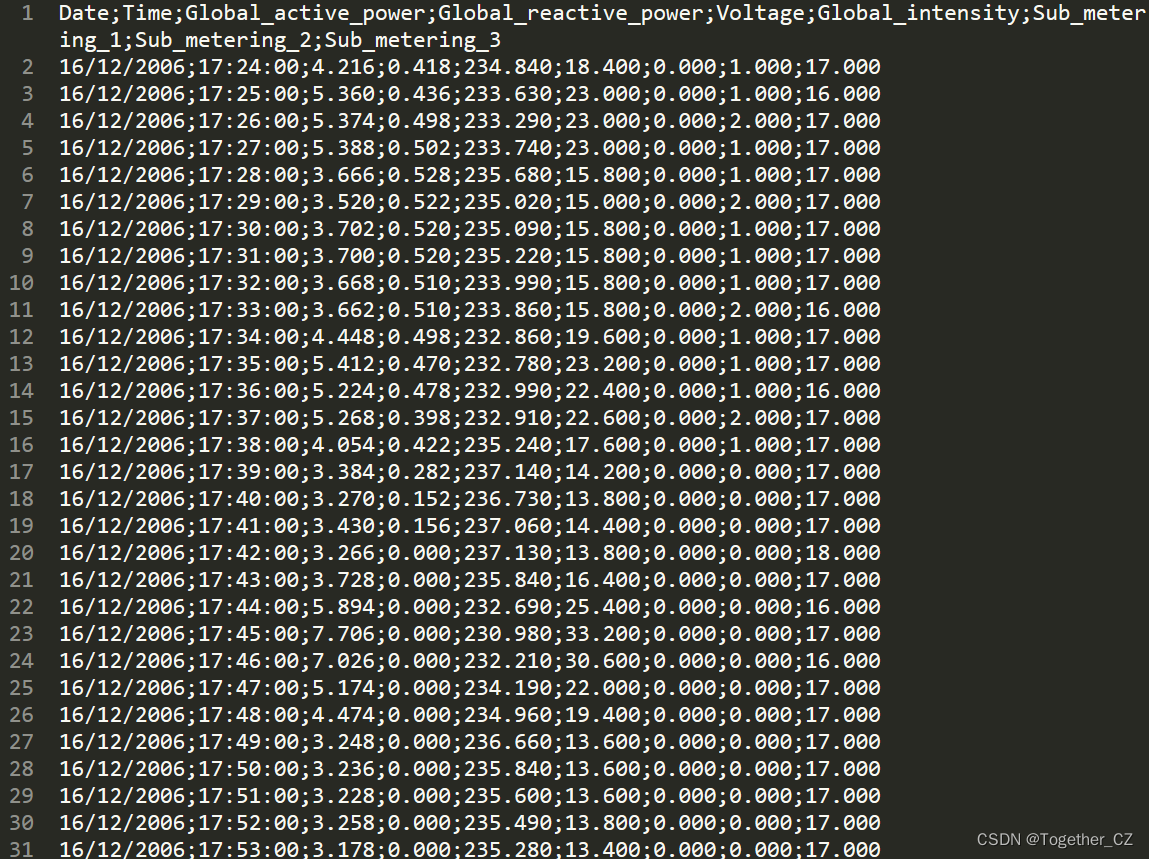
首先就是需要加载读取数据集,这里可以直接使用Pandas实现如下所示:
def loadData(data="household_power_consumption.txt"):
"""
加载数据集
"""
df=pd.read_csv(data,sep=";")
print(df.head(10))
for one_name in names[2:]:
df[one_name].fillna(df[one_name].mean(), inplace=True)
data_list=df.values.tolist()
return data_list加载本地数据集的同时,基于均值对不同列数据进行了填充处理,这里对于数据填充的处理可以使用其他的方式,比如pandas内置的众数、中位数、指定值、均值填充等等都是可以的,在我之前做环保大脑项目的时候其实我们对时序数据有着更细粒度的处理方式。主要分为:滑动窗口数据填充、移动加权数据填充、卡尔曼滤波数据填充几种方式,不同填充算法对比效果图如下所示:

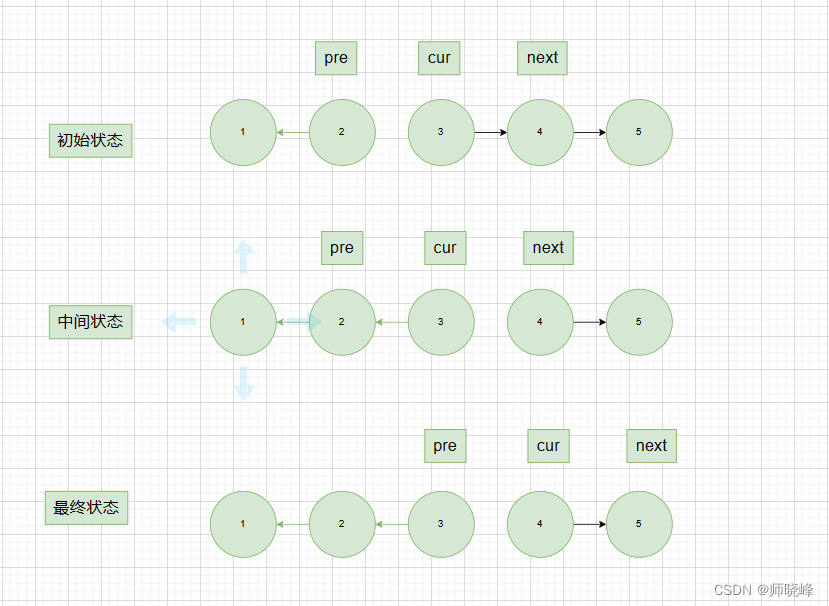
在这里考虑到时间的问题,我主要是使用了比较常用的滑窗数据填充算法,填充原理示意图如下所示:

这种方式在时序数据的缺失值填充上面更为细粒度,不是单纯粗暴地直接使用均值、中位数之类的数据来进行缺失值的填充处理。
代码实现如下所示:
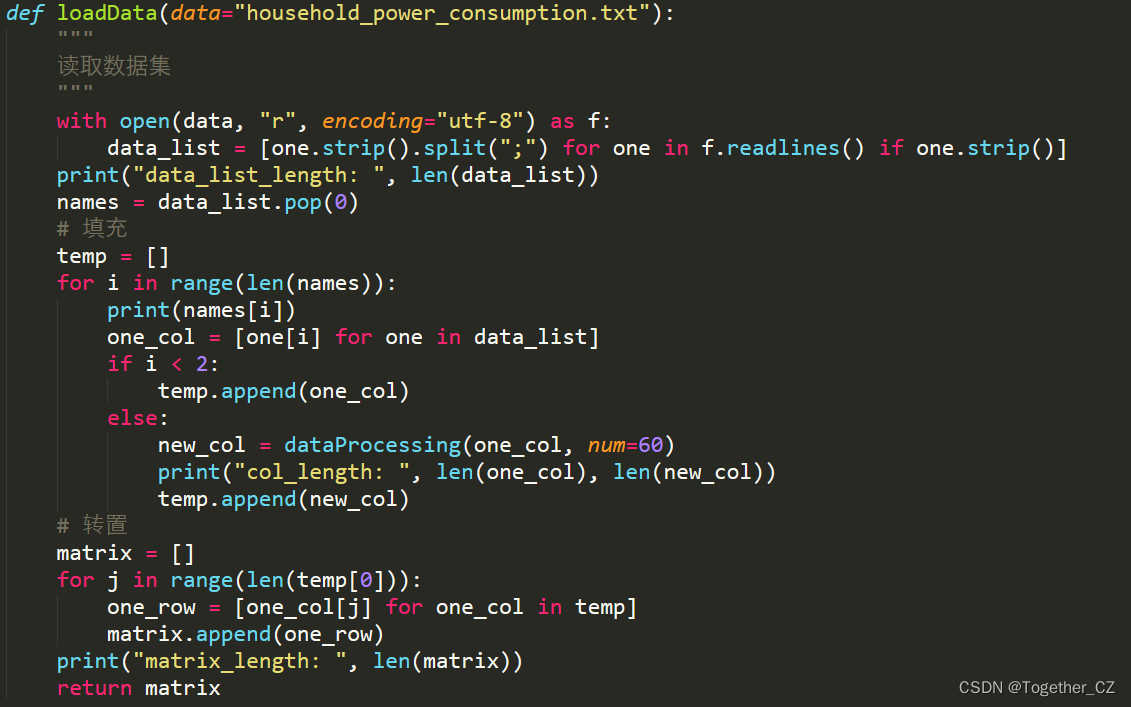
dataProcessing提供的就是因子数据的填充处理计算,之后将填充处理后的因子数据经过转置处理得到新的经过填充处理后的数据集。
接下来我们先对原始数据集进行简单的可视化,如下所示:
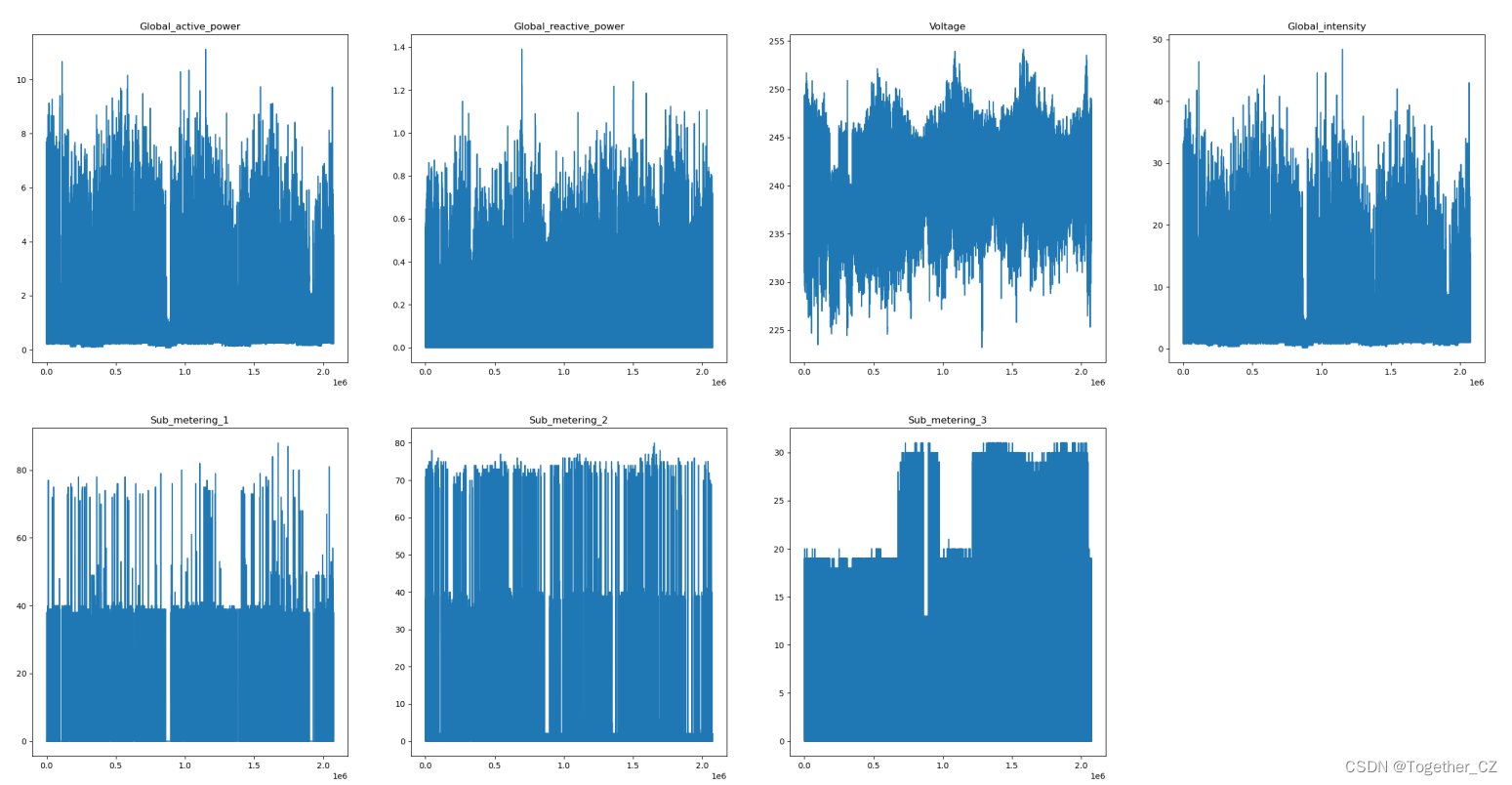
除去前两列是时间列后一共有7个数据列,这里对其进行了整体的可视化,因为200多万的样本数据量导致可视化出来的图像非常的稠密难以看清整体的走势,这里对数据进行抽稀处理,绘制小时粒度的数据曲线,如下所示:
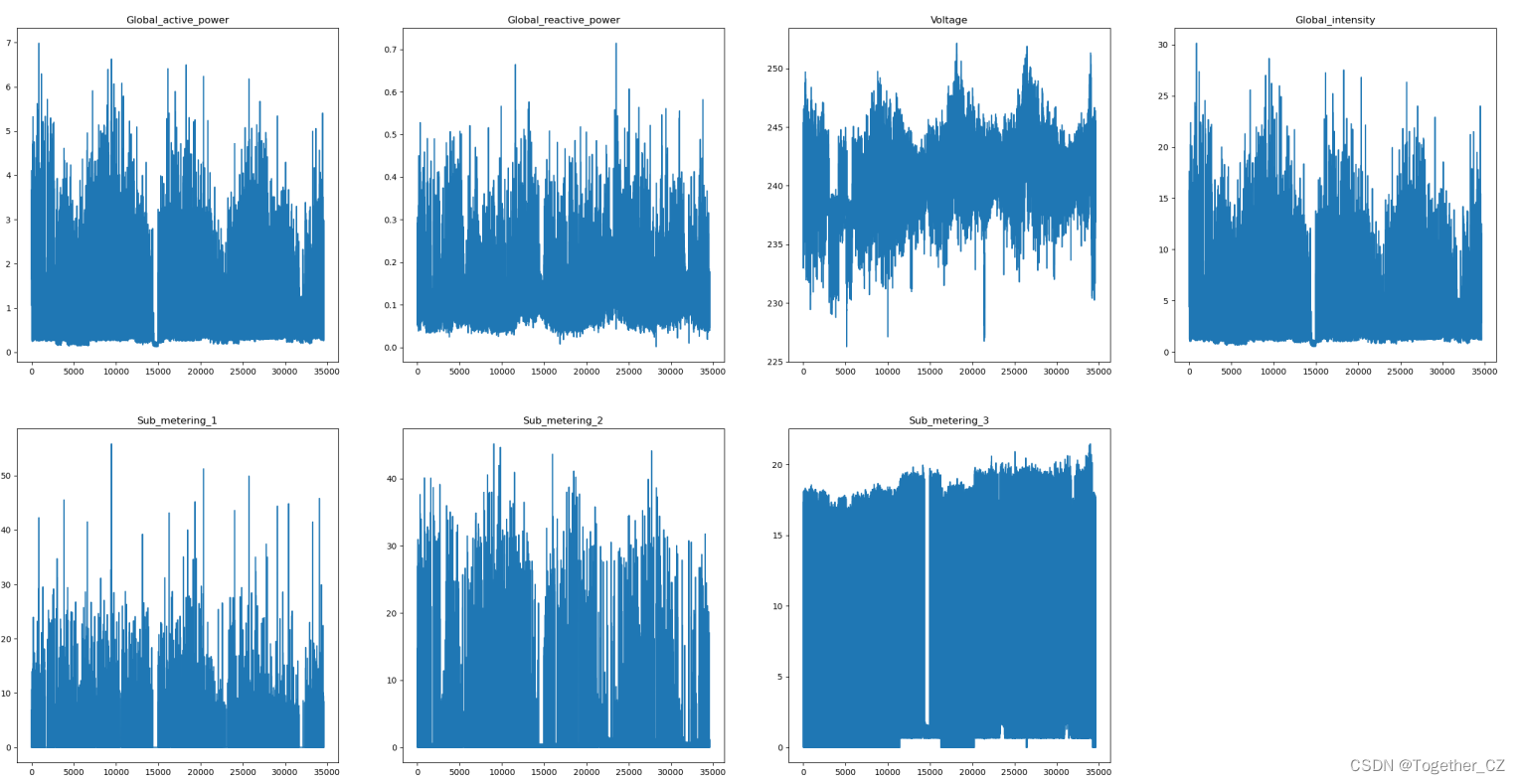
可以看到:整体数据走势还是比较稠密的,需要继续抽稀处理。
同样的处理思路,我们可以绘制日粒度的数据曲线,如下所示:
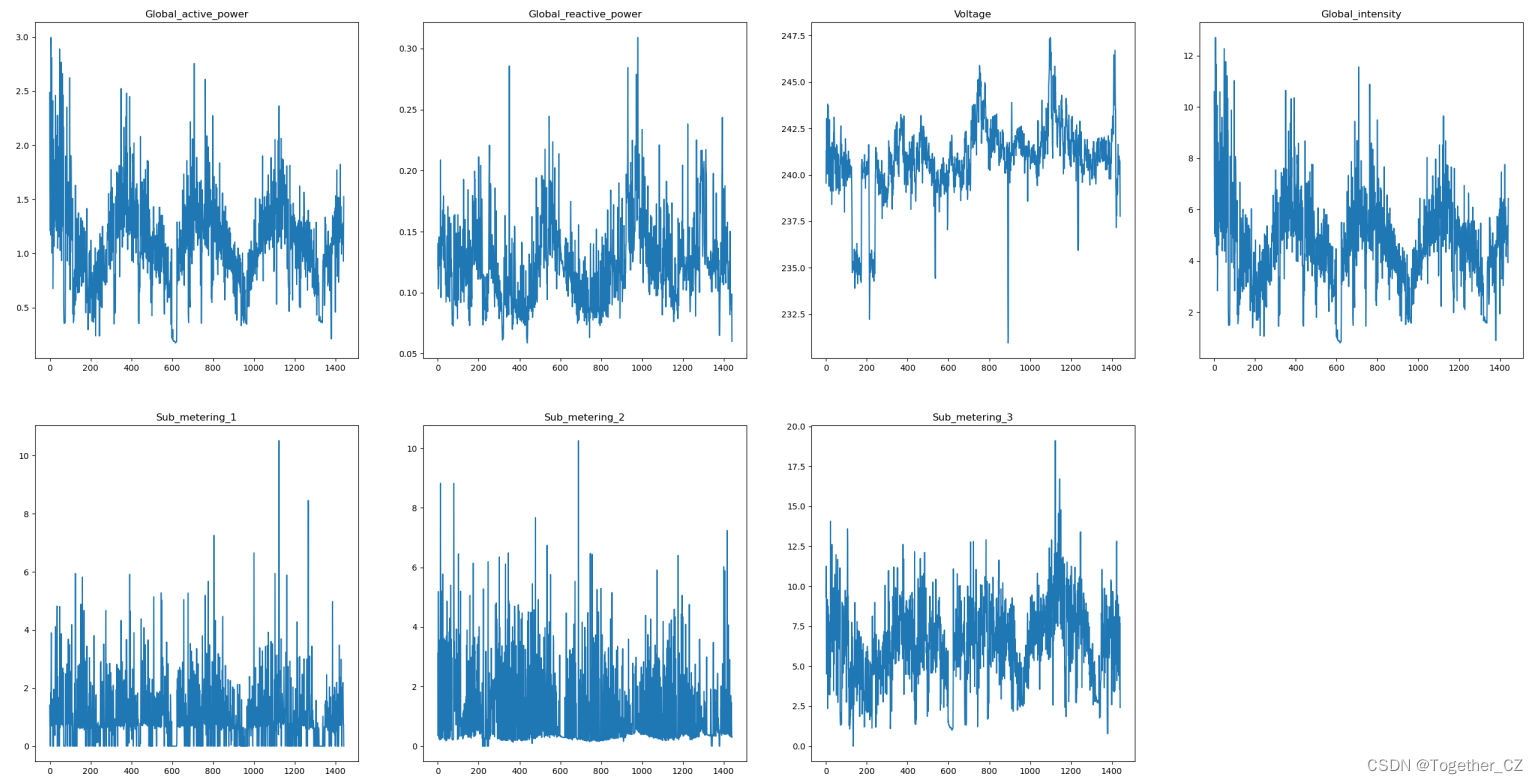
日粒度的数据就已经比较清晰可见了,从不同因子数据走势来看,数据呈现出来的周期性还是比较明显的。
接下来想要对不同因子数据进行挖掘分析计算变量之间的相关性关系绘制热力图,如果这块实现有问题的话可以参考我前面写的文章:
《基于seaborn的相关性热力图可视化分析》
《Python基于seaborn绘制喜欢的热力图,不同色系一览》
《python实践统计学中的三大相关性系数,并绘制相关性分析的热力图》
代码实现和结果实例都是很详细的,相信能够帮你实现这部分的功能。
相关性热力图主要是基于不同变量之间的相关性值进行的可视化,本质就是需要计算变量之间的相关性,这里我常用到的相关性算法主要就是:皮尔斯系数、斯皮尔曼系数和肯德尔系数,当然海鸥其他的方法可以使用可以根据自己的爱好去选择即可。这块代码核心实现如下所示:
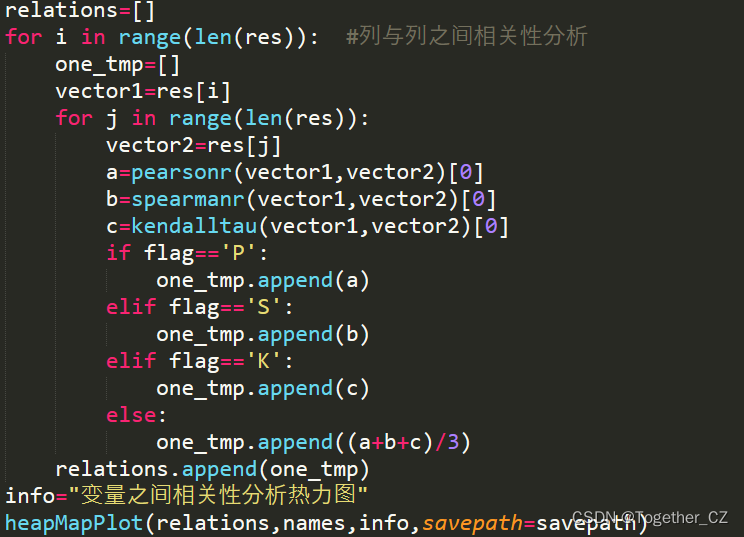
提供了四种方式可选,分别是单独方法以及简单的加权方法实现,接下来我们以日粒度的数据来看下可视化分析结果:
【皮尔斯系数】

【斯皮尔曼系数】
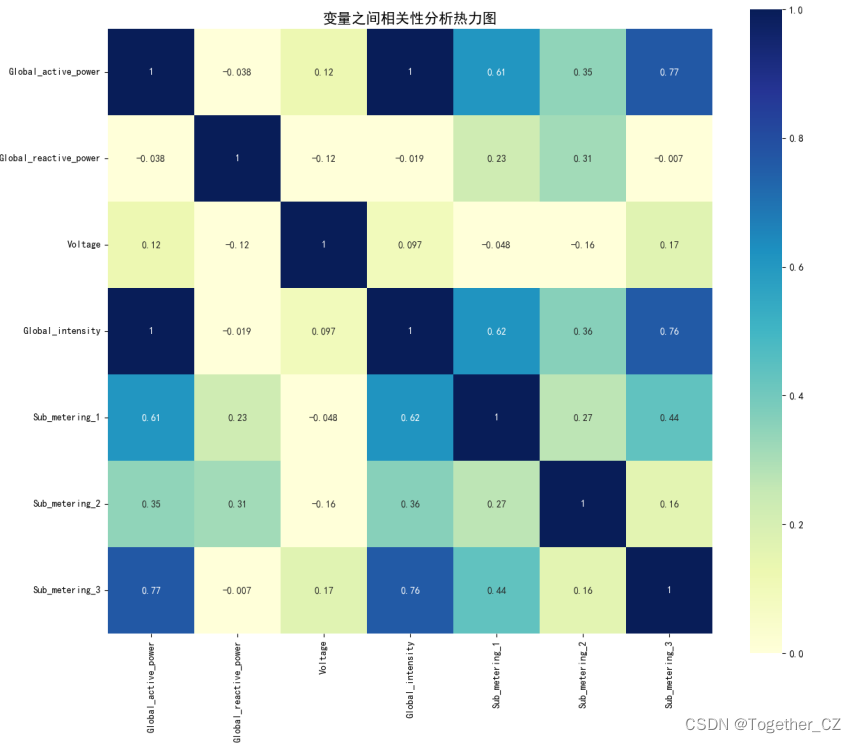
【肯德尔系数】
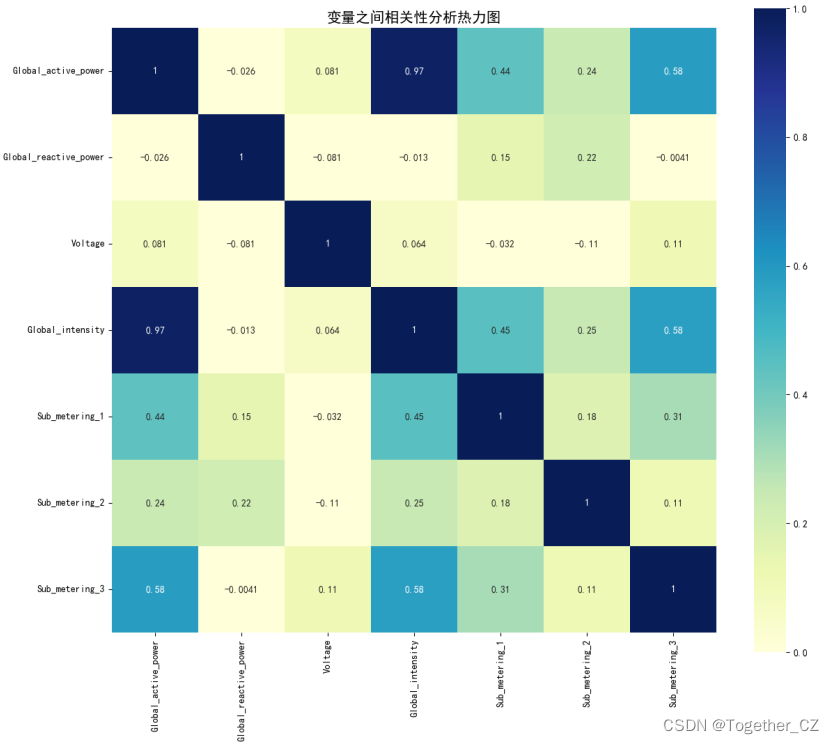
【加权平均方法】
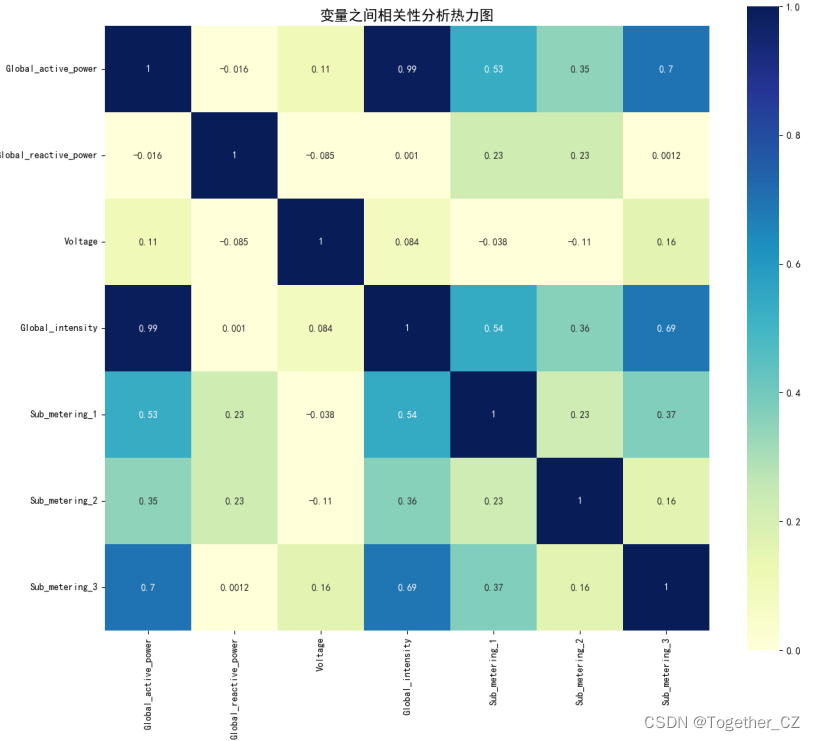
可以看到:不同计算方法计算得到的结果略有不同,但整体趋势是相同的。
Global_active_power和Global_intensity高度相关
Global_active_power和Sub_metering_1、Sub_metering_2、Sub_metering_3相关程度都是较高的
简单的数值分析就到这里,从热力图中还能找到其他的关系这里就不再展开描述了。
接下来我们来尝试对不同时段以及不同日期比如(工作日、非工作日、节假日)进行分析,尝试理解不同时间粒度上用电量的特点。代码实现如下所示:
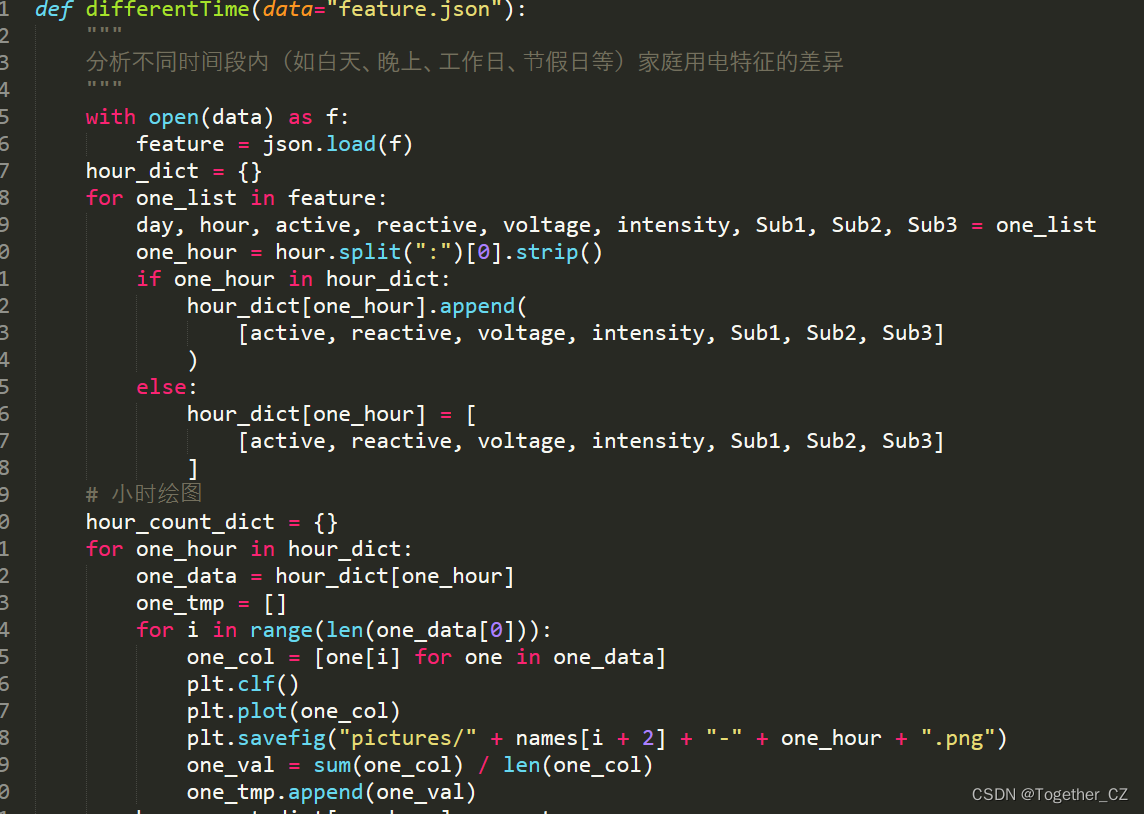
我们先来看小时粒度上,数据呈现出来的差异:
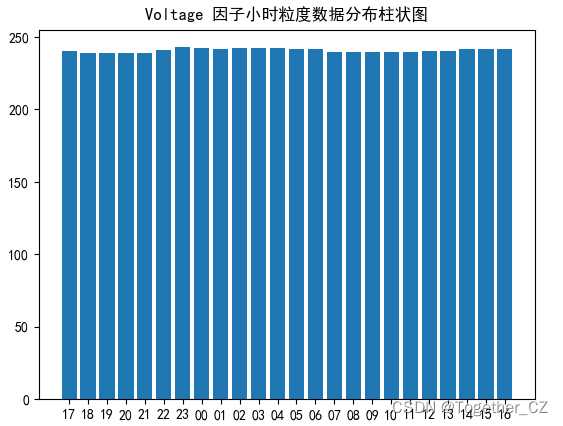
电压的话还是比较稳定的,不同小时粒度上面几乎没有什么差异。
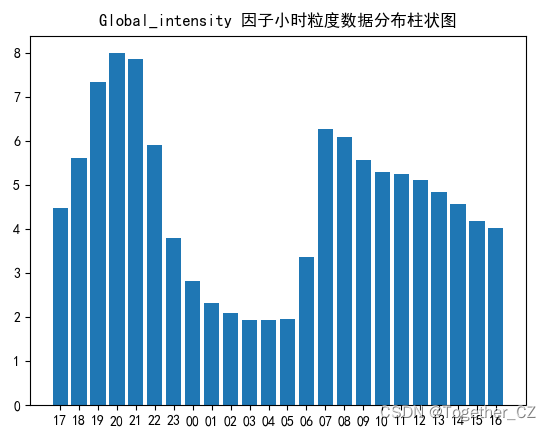
Global_intensity整体呈现出来的差异还是比较明显的,在深夜凌晨期间偏低。
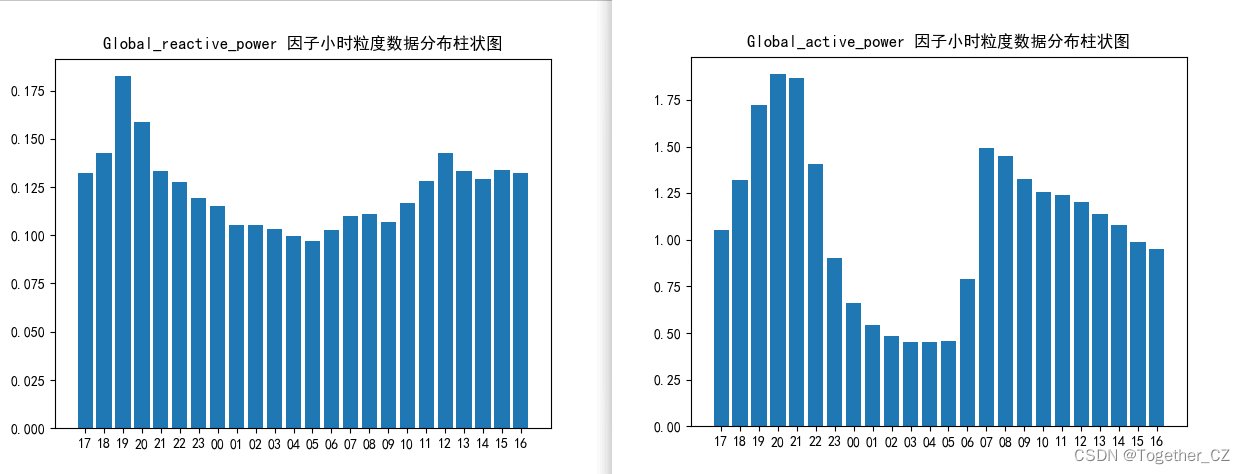
global_active_power和global_reactive_power整体呈现出来的趋势也有类似的表现。
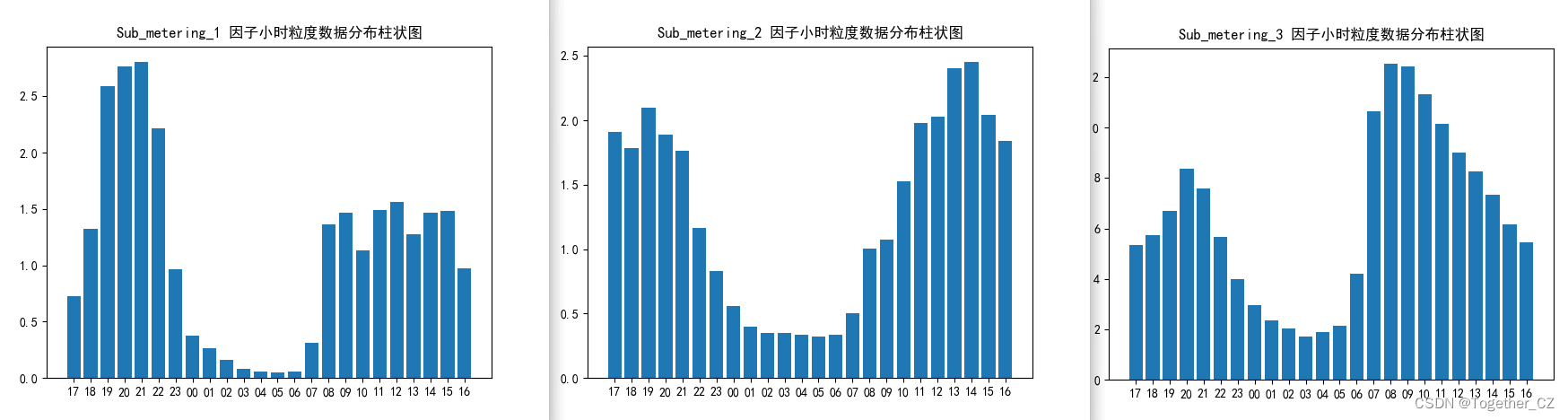
Sub_metering_1、Sub_metering_2、Sub_metering_3整体呈现出来的走势也是基本一致的。
接下来我们来看白天-黑夜两个时段维度上数据整体呈现出来的差异性。代码实现和小时粒度是相似的这里就不再赘述了。
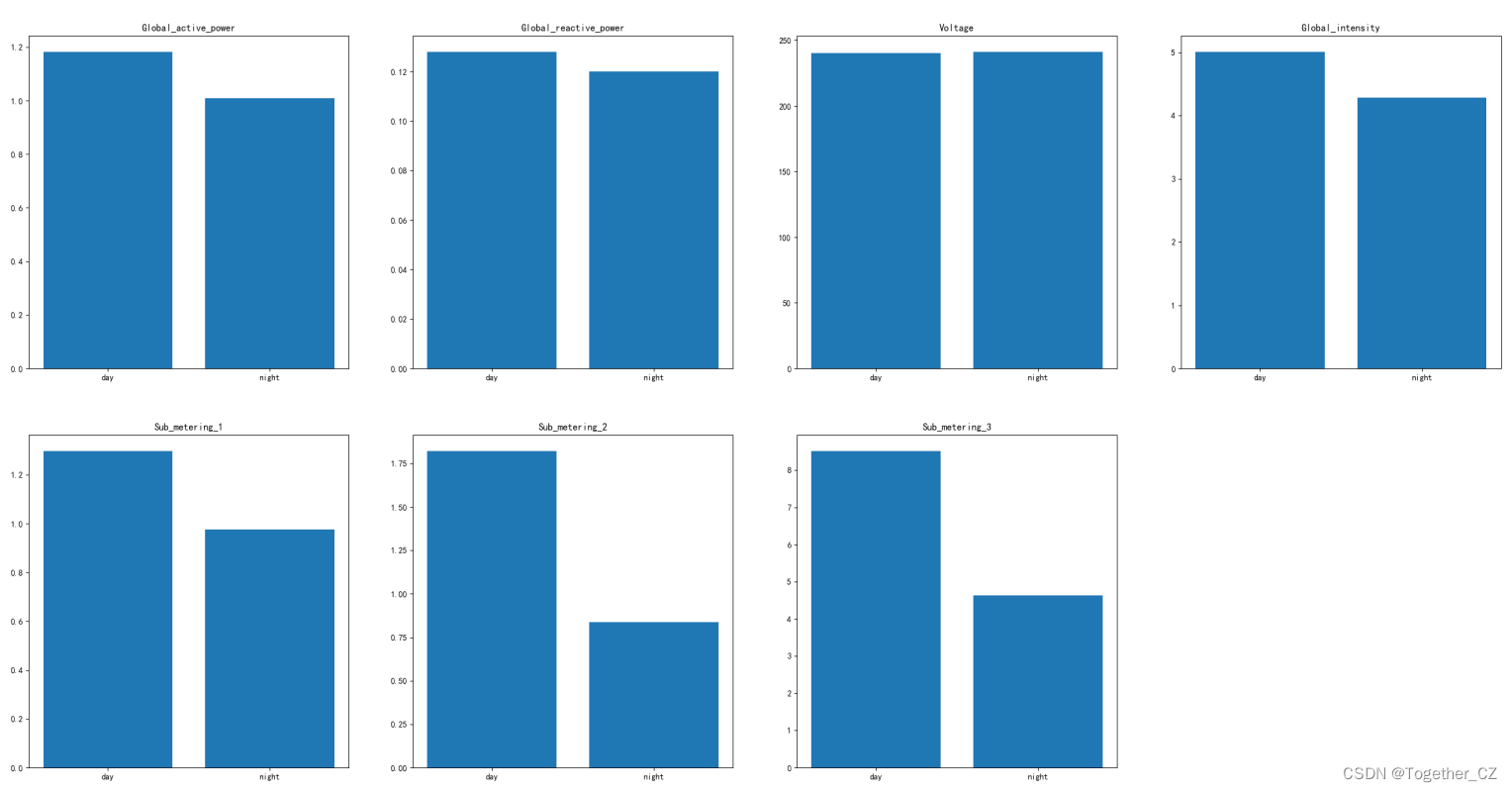
我将其绘制在一张图表上面看起来更加直观一些,这里要注意的一个点就是白天和黑夜的时段划分不同人的理解可能是不一样的,我这里的设置是:
day_list=["08","09","10","11","12","13","14","15","16","17","18"]
night_list=["00","01","02","03","04","05","06","07","19","20","21","22","23"]这里其实还可以进一步细化,比如:不同季节的白天和黑夜时段又是有区别的,当然这里时间的缘故就不再细化了。
最后我们想探索下在工作日、休息日、假节日不同的时间段内用电量的差异情况,整体实现是完全一致的,这里我们直接来看结果就行,这里我一共划分了三个粒度:工作日、非工作日和节假日,如下所示:

工作日和非工作日的时段上用电的变化较为明显,非工作日和节假日因为本身时间段上就是有重叠的,数据呈现出来的趋势也是比较相近的,最后为了直观呈现,将其同样绘制在一起,如下所示:
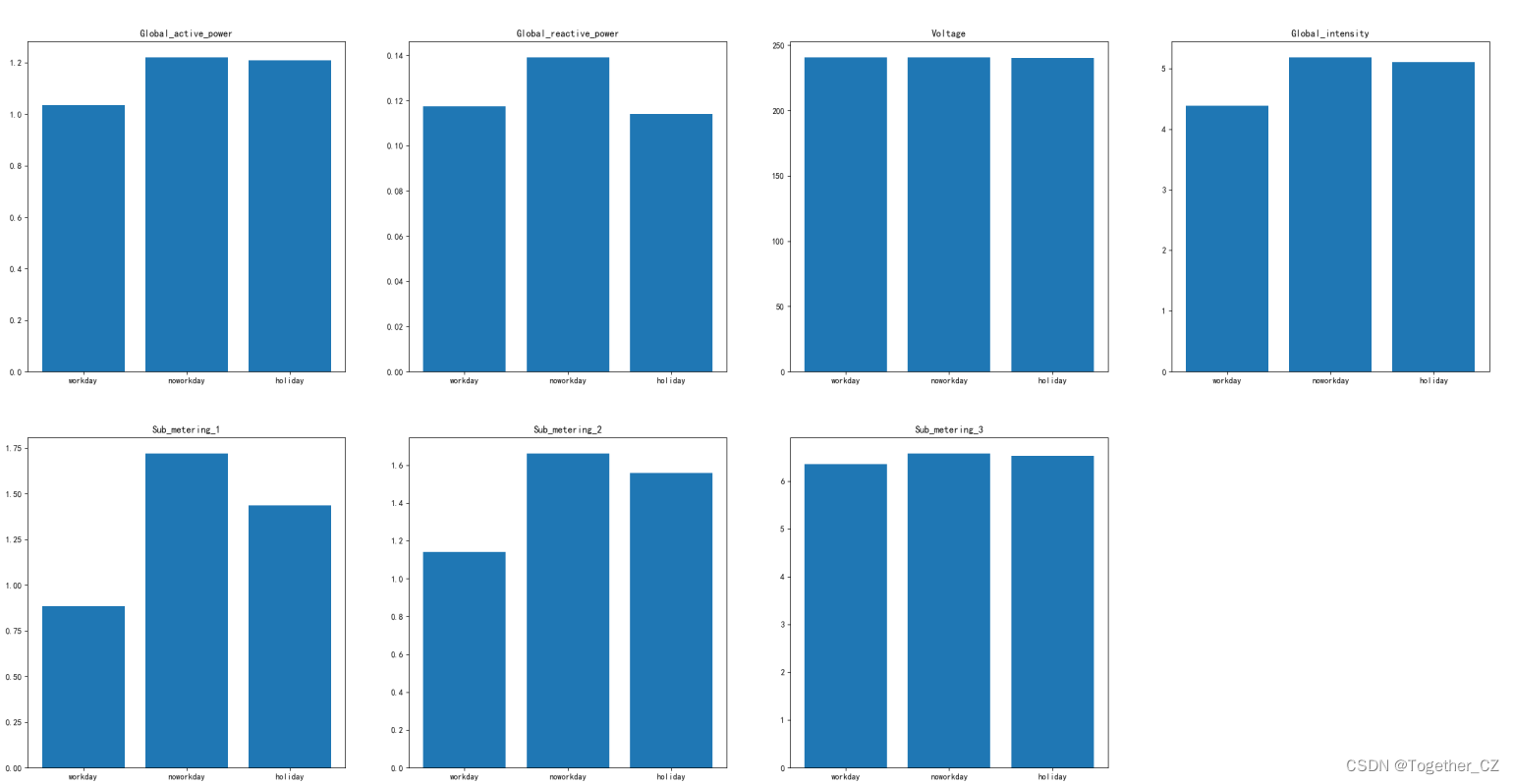
到这里,数据处理和EDA基本就结束了,接下来的主要内容就是想要基于模型来实对未来用电量数据的预测建模分析。时间序列预测类型的任务中主要的预测类型有两种:单变量预测和多变量序列预测,不同的方法适用场景或者说是开发目的也不同,结合前面我们数据热力图分析来看,这里使用多变量序列预测模型更为合适。
在前面的步骤中我们已经解析处理好了原始的数据集存储在feature.json文件中,这里就可以直接进行使用了,加载数据集的同时对原始数据集进行了抽稀处理,不然模型的训练会极为耗时,之后对数据进行了归一化处理,来消除不同量纲带来的影响,提升模型后续迭代收敛速度的同时也有助于模型精度的提升,这部分代码实现如下所示:
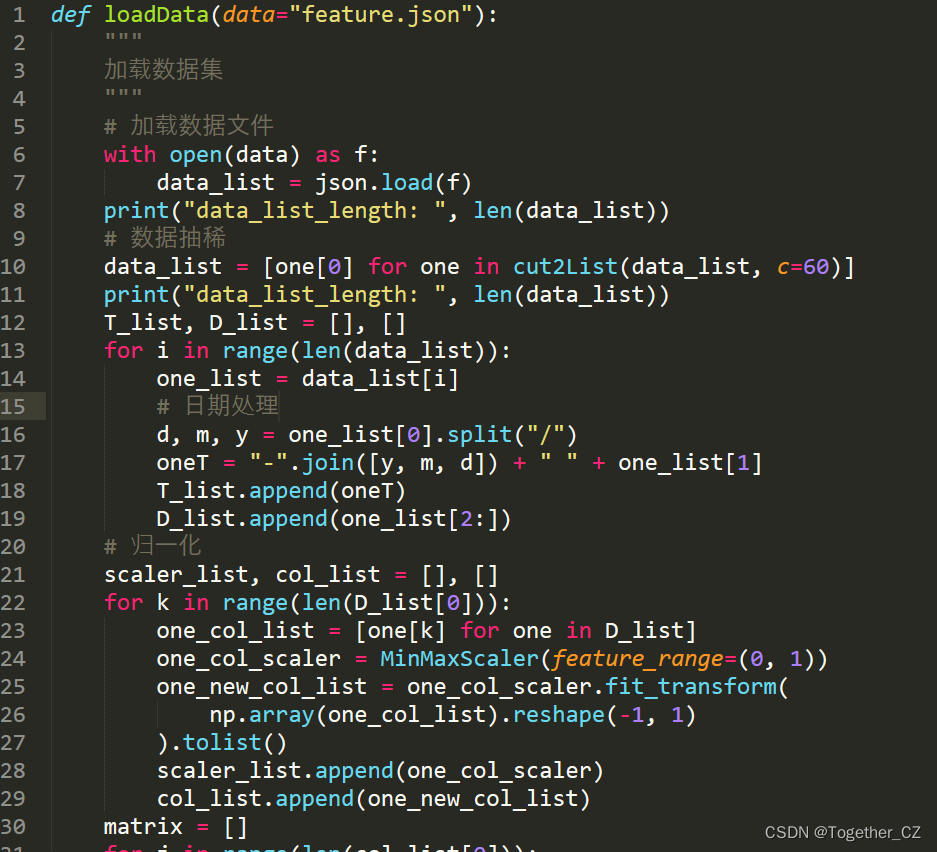
接下来就可以创建数据集,时序数据本身是序列的数据,常用的方式就是基于滑动窗口来进行数据集的创建,原理示意图如下所示:
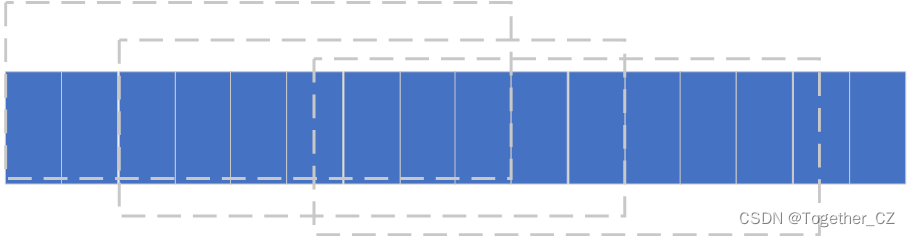
也可以自由的设定步长和间隔从而动态地调整获得的数据集shape。
接下来就可以初始化构建模型了,模型的选择性就比较广了,可以单独地使用LSTM、RNN、GRU、CNN之类的模型也可以使用模型的组合,比如CNN-LSTM、CNN-GRU等等都是可以的,这里时间的问题就不再一一去做实验了。
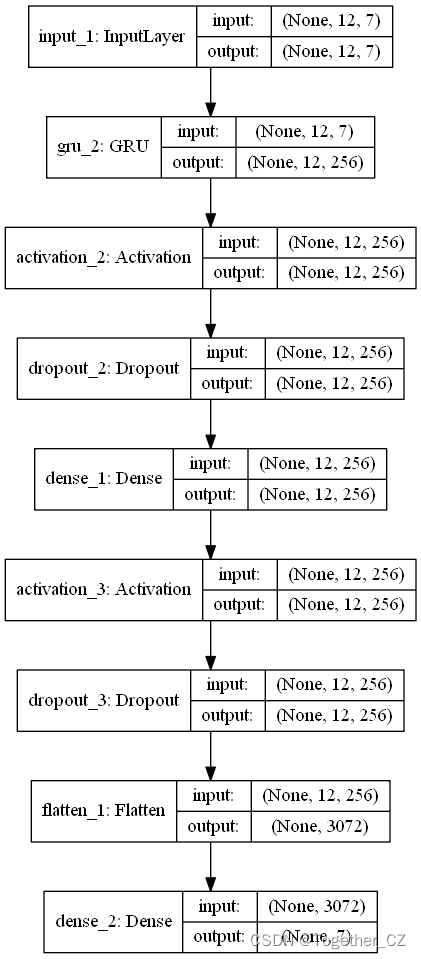
CNN-GRU模型结构图如下所示:
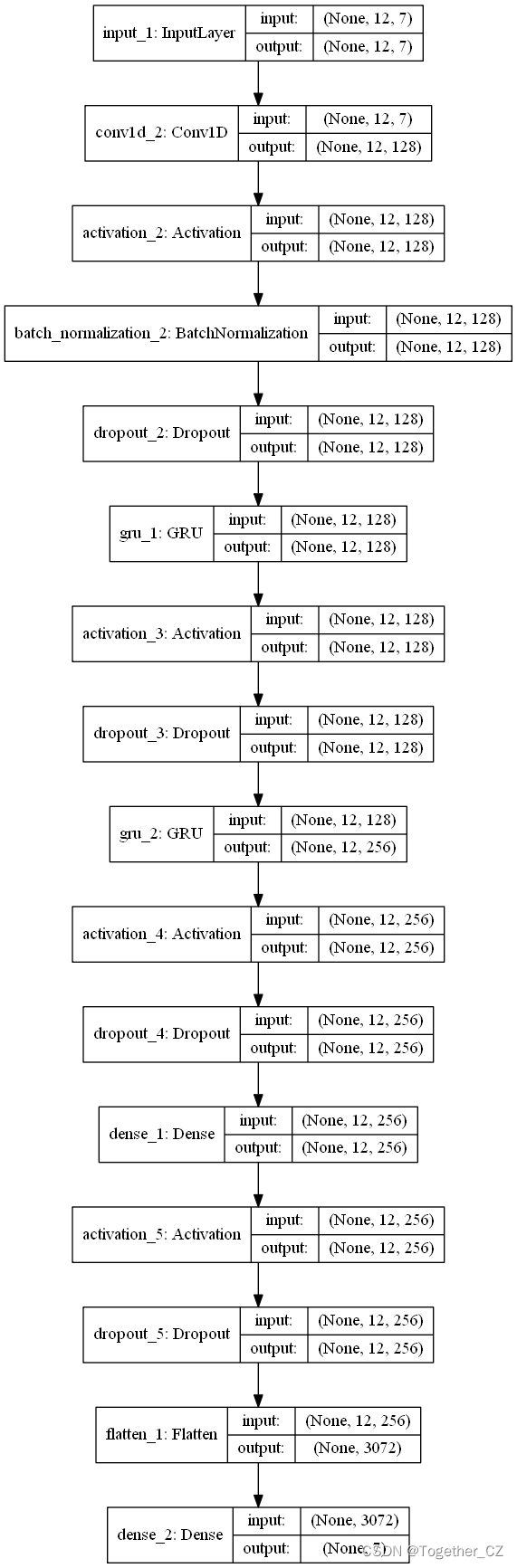
模型训练日志输出如下所示:
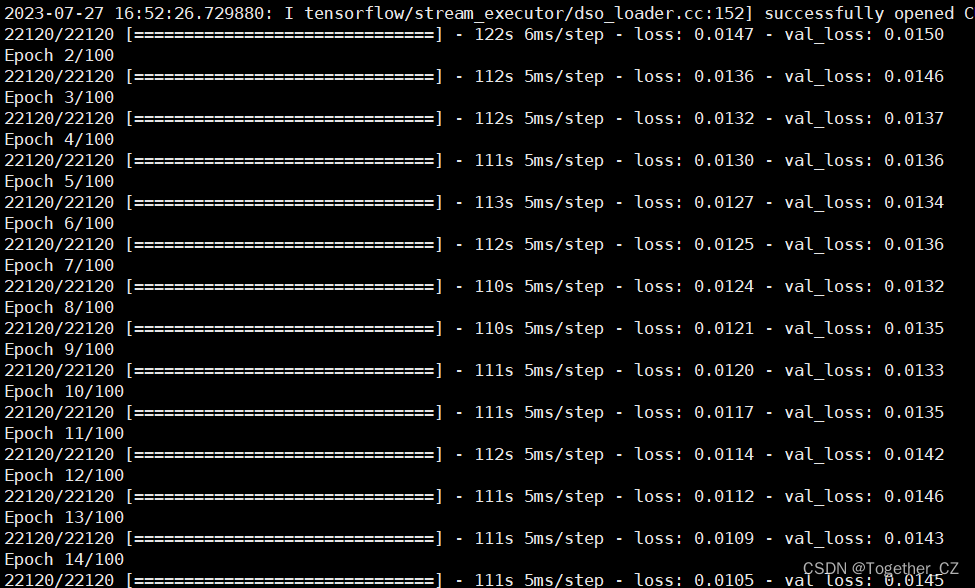
为方便对模型进行评估和可视化,实现了专用的方法,在我之前的文章中其实都有的,这里简单看下就行:
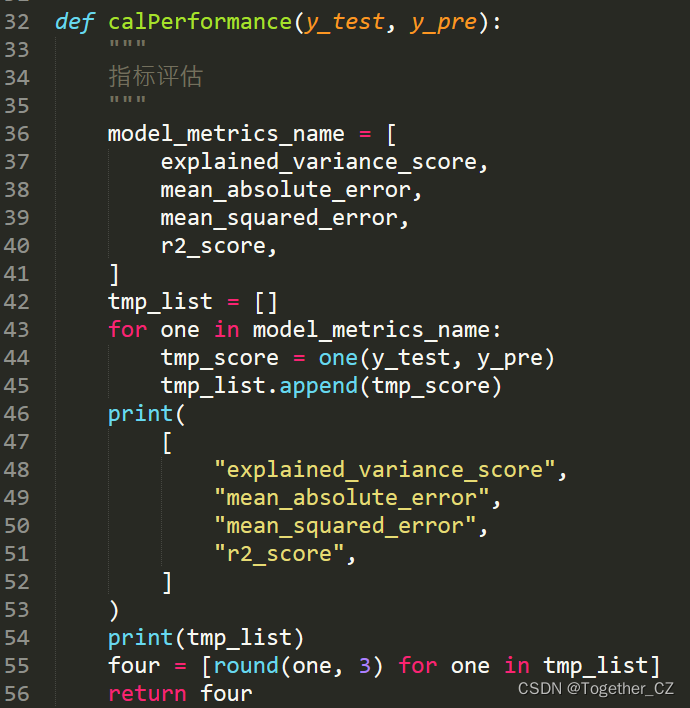
loss可视化:
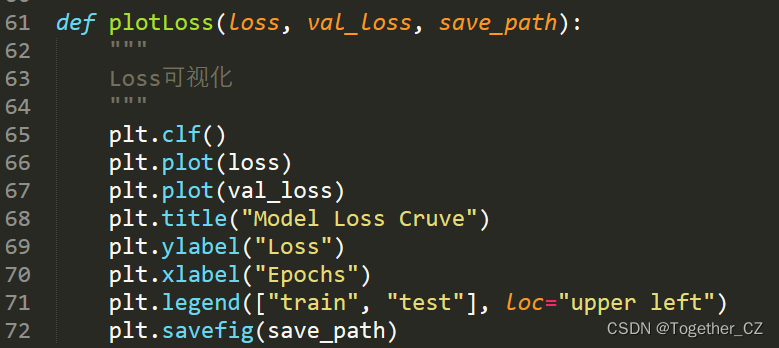
当然了如果是单独使用GRU之类的模型也是可以,这里同样也做了下:
最后我们想要挖掘不同时段用电特征的不同,需要基于Kmeans算法来完成这一工作,K-Means算法是一种常用的无监督学习算法,用于将数据集划分为K个不同的簇(cluster)。每个簇都具有相似的特征,并且簇内的数据点彼此之间更加接近。以下是K-Means算法的详细步骤:
选择K个初始质心:从数据集中随机选择K个数据点作为初始质心。
分配数据点到最近的质心:对于每个数据点,计算其与每个质心之间的距离,并将其分配给距离最近的质心所属的簇。
更新质心位置:对于每个簇,计算该簇所有数据点的均值,并将其作为新的质心位置。
重复步骤2和3,直到质心位置不再发生变化或达到预先定义的迭代次数上限。
最终聚类结果:得到最终的簇划分结果,每个数据点都被分配到一个簇中。
K-Means算法的目标是最小化簇内数据点与质心之间的平方误差和(Sum of Squared Errors, SSE)。通过迭代优化质心位置,算法试图找到使SSE最小化的最佳簇划分。
K-Means算法的特点和注意事项:
K值的选择:K是作为输入参数提供给算法的,需要根据实际问题和经验来选择合适的值。不同的K值可能会导致不同的聚类结果。
初始质心的选择:初始质心的选择可以影响最终聚类结果,因此应该注意使用随机种子或多次运行算法以避免局部最优解。
数据预处理:在应用K-Means算法之前,通常需要对数据进行标准化或归一化处理,以确保各个特征具有相似的重要性。
尽管K-Means算法在许多场景下表现良好,但也存在一些限制:
对初始质心位置敏感:初始质心的选择可能影响最终结果,且算法可能陷入局部最优解。
处理非球形簇困难:K-Means算法假设簇是凸形并且具有相同的方差,因此对于非球形的、大小不一的簇效果可能较差。
需要指定K值:K值的选择通常是主观的,并且较大的K值可能会导致过度拟合。
这里需要确定合适的聚类中心数K,常用的方法就是手肘法。
手肘法(Elbow Method)是一种常用的方法,可用于帮助确定K-Means聚类算法中最优的聚类数量。它基于聚类的SSE(Sum of Squared Errors)或误差平方和来评估不同K值下的聚类效果。以下是使用手肘法确定最优聚类数量的步骤:
在给定范围内选择K值:首先,选择一个合适的K值的范围,例如从2开始到预设的最大聚类数量。
计算每个K值对应的SSE:对于每个K值,在数据集上运行K-Means算法,并计算该K值下的SSE。
绘制SSE与K值的关系图:将每个K值对应的SSE绘制成折线图或曲线图。
寻找“手肘点”:观察SSE与K值的关系图,寻找一个明显的拐点或“手肘点”,即在该点后进一步增加K值所获得的SSE减少幅度较小。
确定最优的聚类数量:选择手肘点对应的K值作为最优的聚类数量。
需要注意的是,手肘法并不总是能够明确地指出最佳的聚类数量,尤其当数据集没有明显的手肘点时。在这种情况下,可以结合其他评估指标、领域知识和实际问题考虑选择适当的聚类数量。
这里我们基于日粒度的数据采用手肘法绘制了对应的曲线如下所示:
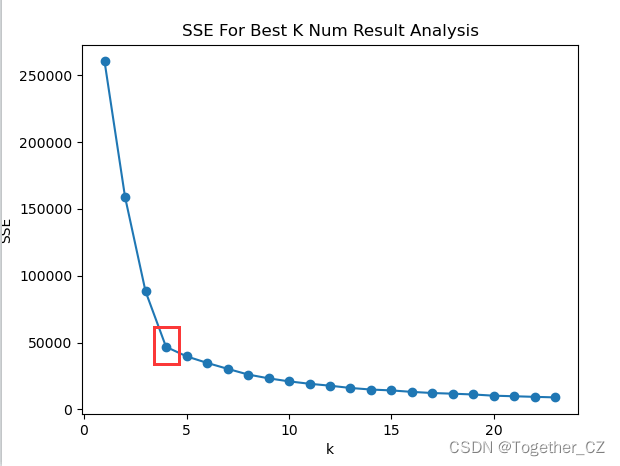
结合结果图分析这里考虑最优的聚类中心数为4。
接下来就设定聚类中心为4来进行聚类计算,Kmeans的使用还是很简单的可以直接使用sklearn内置的模块即可,如下:
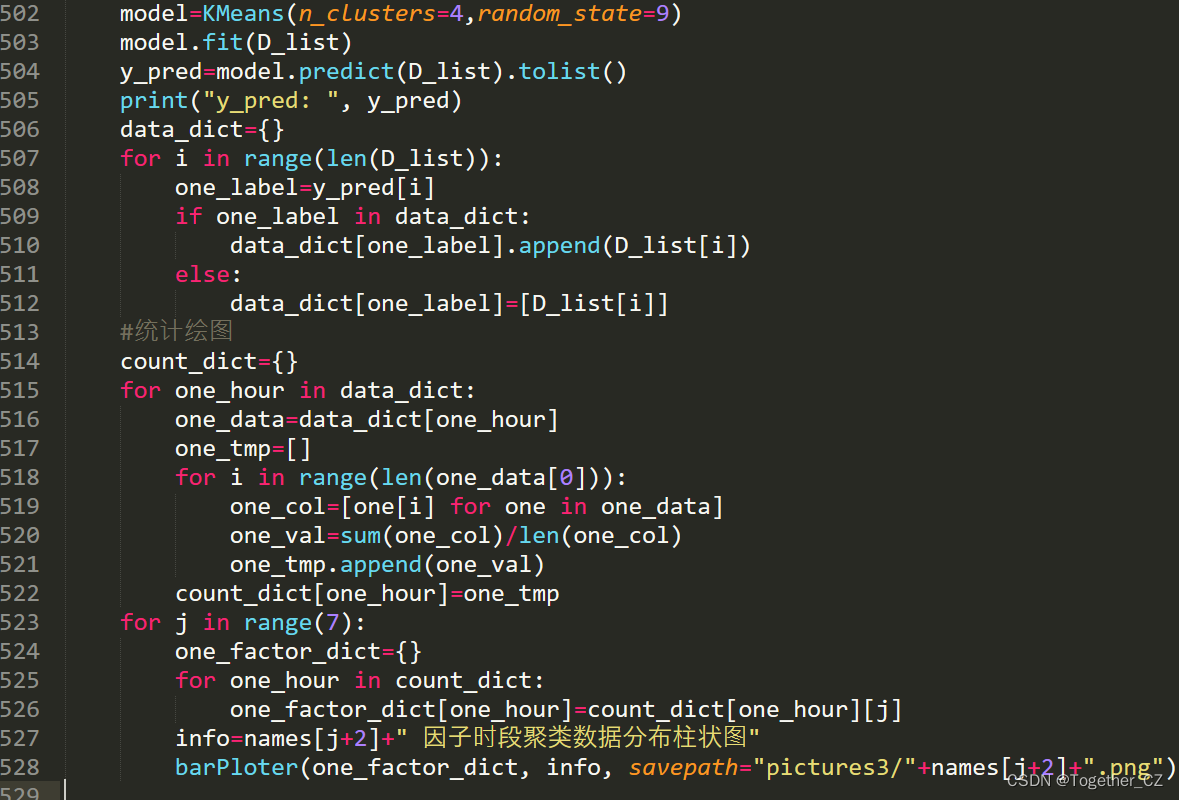
这里绘制了7个因子经过聚类后的数据结果图,如下所示:
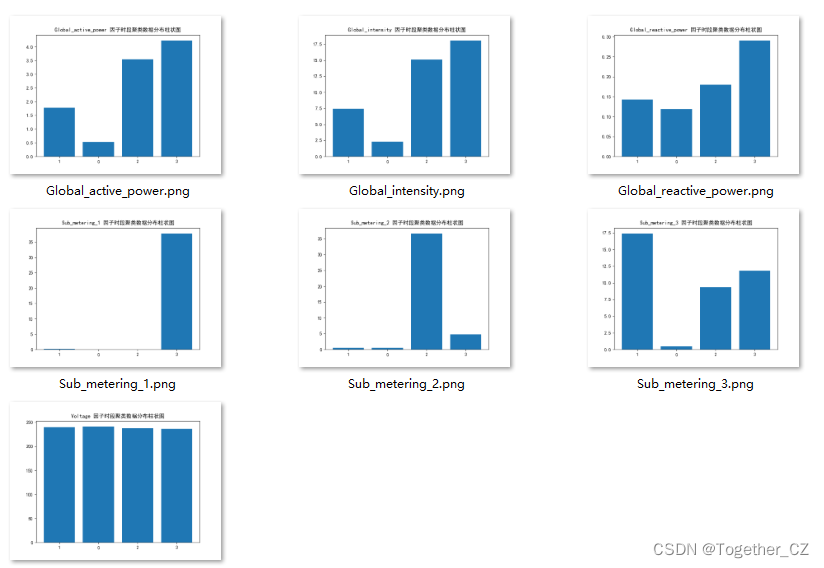
电压的话应该一直都是保持几乎不变的状态,Global_active_power、Global_reactive_power、Global_intensity以及Sub_metering_3呈现出来的差异还是比较明显的。
不知不觉也写了挺久了,算是整体流程记录下。