题目
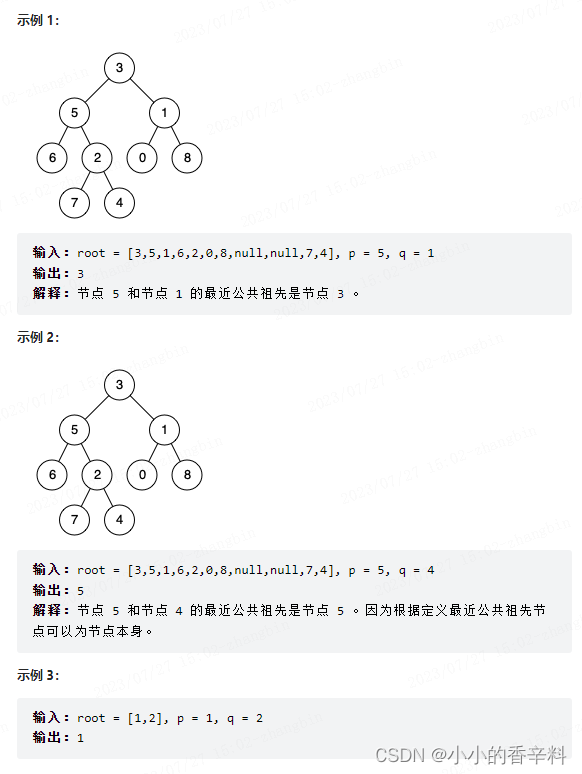
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
思路
这题的难点在于:
- 如何建立每个节点与它的两棵子子树之间的关系,用什么遍历方式?
- 找到答案之后,怎么返回?判断条件是什么?
解决了这两个问题,这道题也就不难了。
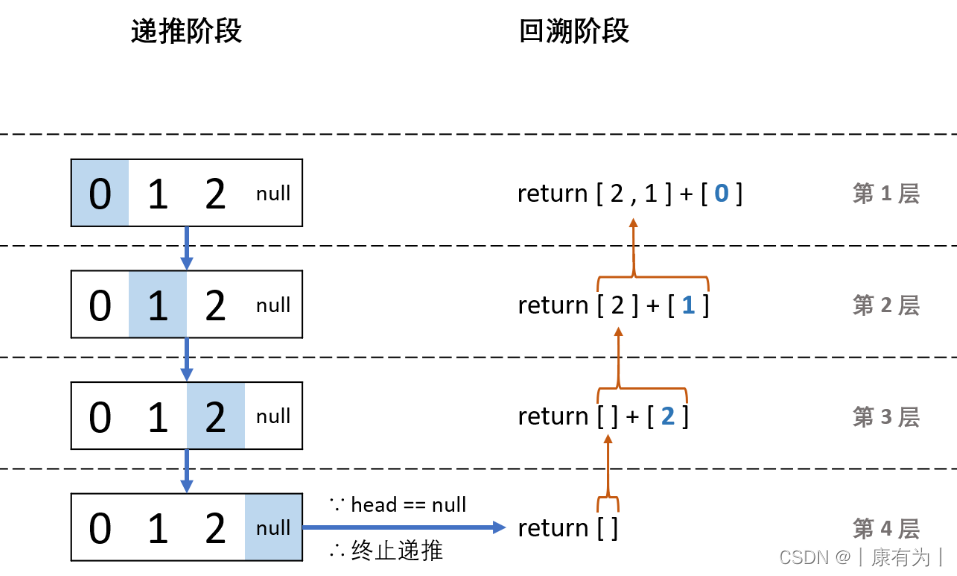
首先思考第一个问题,我们该用什么遍历方式?试想一下,如果用前序和中序,顺序是自顶向下的,那当我们找到p和q时,怎么返回他们的最近公共祖先节点呢?无法找到了吧!所以我们希望遍历的顺序时自底向上,先找到p和q,再去找他们的公共祖先并返回。这其实就是一种回溯的思想,我们理所当然应该想到后序遍历。为什么后序遍历能做到回溯?因为后续是左右根,也就是先不断地递归调用自身的左右子树,在这个递归过程中的状态会被内部栈存储起来,直到遇到递归出口,才执行左右根中“根”的逻辑,执行完毕从栈中弹出当前状态,返回到上一层节点的状态,不断重复这个过程向上回溯。所以利用后序遍历找到p和q很容易。
第二个问题,找到p、q之后如何处理?我们可以通过后序遍历的递归过程(自顶向下)去找到p和q所在的节点位置。接下来我们这样处理,如果遇到p和q或者root为空,则直接返回自身。然后开始回溯,如果left和right有一个不为空则返回不为空的那个,不为空的那个节点一定是p和q的最近公共祖先。因为当前已经找到p和q了,并且是自底向上回溯,而在递归过程规定了只有遇到p和q才不会返回空,所以遇到的第一个left和right都不为空的root就是我们要找的最近公共祖先。如果left和right都为空,则直接返回空。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
# 根节点为空或者遇到p、q则应该返回当前节点
if not root or root==q or root==p:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
# 当遇到第一个left和right不为空的节点就是答案
if left and right:
return root
# 如果有一个不为空,应该直接返回不为空的节点,因为它实际上就是我们要找的答案,最后要返回到根节点所在层
if not left and right:
return right
elif not right and left:
return left
# 都为空返回空
else:
return