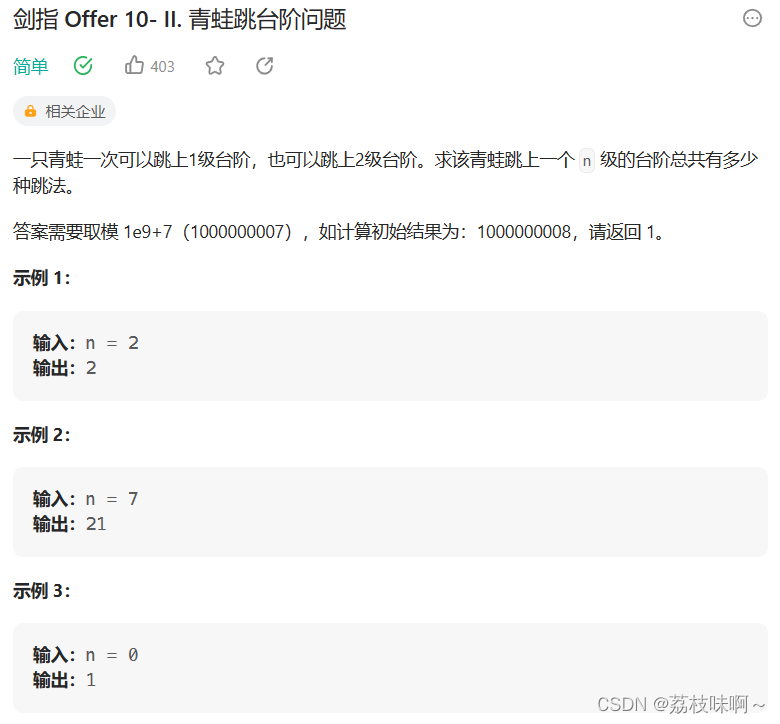
这道题和上一道斐波那契一模一样，如果你要到达第n个台阶，你有两种方法，第一种是到达n-1级然后跳一下，第二种是到大n-2级然后跳两下，所以到达n级的方法数就是到达n-1级的方法数加上到达n-2级的方法数。其实就是和斐波那契数列一样只不过前两个数不一样。

动态转移方程：dp[i] = dp[i-1] + dp[i-2];

初始状态：dp[0] = 1; dp[1] = 1;

返回值：dp[n];

class Solution {
    public int numWays(int n) {
        if(n==0)return 1;
        if(n <= 2){
            return n;
        }
        int p=1,q=2,r=0;
        for(int i=3; i<=n;i++){
           r = (p+q) % 1000000007;
           p = q;
           q = r;
        }
        return r;
    }
}