摘要

知识图谱是一种普遍存在的数据结构，已被应用于许多领域。知识图谱推理是根据知识图谱中已有的信息发现或推断知识。然而，大多数现有的工作都属于 point-wise 方法，这些方法对一条线索执行推理。

point-wise
是一种常见的评估和处理文本数据的方法。Point-wise方法将文本数据转化为单个数据点的形式进行处理和评估。
在文本分类任务中，point-wise方法将每个文本样本视为一个独立的数据点，并为每个数据点分配一个标签或分数。这样，可以使用常见的机器学习算法（如支持向量机、逻辑回归等）对每个数据点进行独立的分类或评分。这种方法的优点是简单直观，易于理解和实现。
例如，在情感分析任务中，point-wise方法将每个句子或文本片段视为一个数据点，并为其分配一个情感标签（如正面、负面、中性）。然后，可以使用分类算法对每个数据点进行情感分类。

知识图谱的比较推理侧重于推断多条线索的共性和不一致性，这是一个新的研究方向，可以应用于许多应用。

在本文中，我们正式给出了比较推理的定义，并提出了几种不同的方法来处理 成对(pairwise) 和集合情况下的比较推理。

pair-wise
和List-wise方法与point-wise方法相对， Pair-wise方法考虑了两个数据点之间的关系，例如比较两个文本的相似性或排序。List-wise方法则将整个数据集作为一个整体进行处理，例如在搜索排序中考虑整个文档列表的排序。

所提出的方法的思想是，我们从知识图谱中找到一个知识片段来最好地表示给定声明的语义，并根据它给出理由。并真实世界的数据集上进行了广泛的实证评估，以证明所提出的方法具有良好的性能。

介绍

知识图谱是一种普遍存在的数据结构，用于存储真实世界的实体及其关系。

自2012年首次亮相以来，已经提出了几种广泛使用的知识图谱，包括Yago、Wikidata、Freebase等。过去几年来，旨在发现或解释现有知识或从知识图谱中的现有信息推断新知识的知识图推理已成为一个重要的研究方向。

尽管在学术界和工业界都取得了巨大的成就，但现有的知识图谱推理工作大多属于point-wise（点式）方法，对一条线索（例如，三元组、多跳查询、复杂查询图）进行推理。例如，在事实核查中，给定一个主张（例如，表示为知识图谱的三元组），它决定该主张是真实的还是伪造的。然而，比较推理很少被研究。不同于点式推理（或在知识图谱上的推理），知识图谱上的比较推理侧重于对多条线索推断共性和（或）不一致性（例如关于一篇新的文章的多条声明），这是知识图谱推理上的新的研究方向并且可以广泛的应用于众多领域，例如事实核查。

与逐点（单一声明）事实核查相比，比较推理具有许多独特的优势。这是因为在许多真实世界的情况下，例如，多模态假新闻检测，单独的单一声明事实核查是不够的，而比较推理提供了关于输入线索的更完整的画面，这反过来帮助用户发现通过逐点方法看不见的细微模式（例如不一致性）。

当我们同时验证两个声明（或三元组）时，如果我们单独评估，即使每个声明(三元组)组本身是一致的，结果也可能不一致。

假设有一篇 多模态新闻的文章 ，我们希望验证它的真实性。为此，分别从给定的新闻中提取了两个查询图。一个查询图形包含来自文本的所有信息，另一个包含来自图像的信息。如果我们执行点式推理来分别检查这两个查询图中的每一个，那么两者似乎都是真的。然而，如果我们同时对两个查询图进行推理，并通过比较，我们可以发现它们之间微妙的不一致性（即，不同的飞机类型，最大飞行距离的差异）。此外，比较推理还可以用于知识图的扩展、集成和完成。

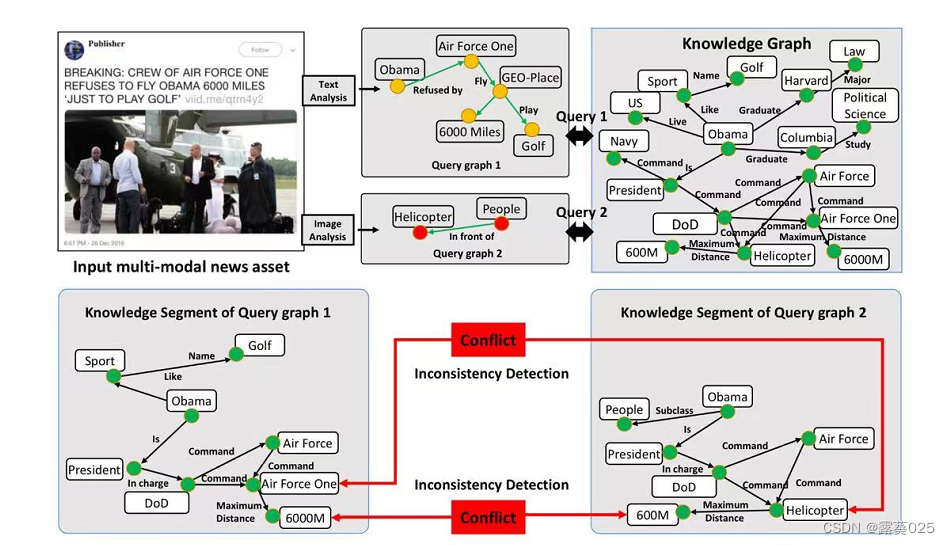
“Multi-modal news”（多模态新闻）
是指结合多种媒体形式（如文本、图像、视频、音频等）来呈现新闻内容的方式。

本文解决了比较推理的问题。主要关注两个问题：成对比较推理和集体比较推理。

具体而言，我们应对以下两个关键挑战：

1. 我们利用图神经网络和图核，根据背景知识图中的信息，揭示输入线索的共性和不一致性。我们提出了几种不同的算法，并证明了它们的有效性。
2. 比较推理的一个常见构建块是知识段，它是给定线索（例如，三元组或其一部分）的一个小连接子图，用于总结其语义上下文。在此基础上，我们提出了实现成对推理和集合推理的核心算法。关键思想是利用知识片段中的结构和语义信息来帮助发现模糊矛盾。

这篇论文的主要贡献：

• 问题定义：我们在知识图上引入了比较推理，它补充并扩展了现有的逐点推理能力。
• 算法：我们提出了一系列比较推理算法，既可以解决成对比较推理，也可以解决集体比较推理经验
• 评估：我们进行了广泛的实证评估，以证明我们提出的方法的有效性。

问题定义

首先介绍符号——本文中将使用的符号，然后介绍其他重要概念和比较推理的正式定义。

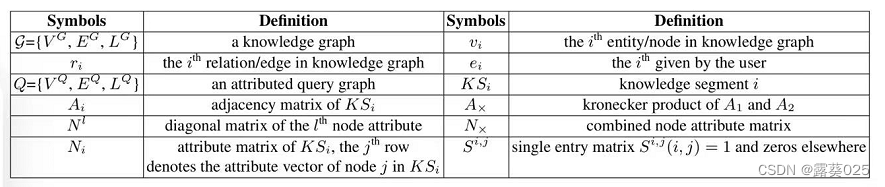
给定多条线索，比较推理的目标是推断它们的共性和（或）不一致性。
如果给定的信息是一对线索，则称之为成对比较推理或成对策略检验。目的是推断这两条线索是否连贯。
如果给定的信息是一个连接的查询图，那么目标是检测给定图内部是否存在不一致。这个问题被称为集体比较推理或集体事实核查。

与传统的点推理方法不同，比较推理可以揭示一些点推理方法可能忽略的微妙模式。以基于知识图的事实核查为例，考虑两种声明（三元组）：（巴拉克·奥巴马，哈佛大学毕业）和（巴拉克·奥巴马，政治学硕士）。即使每一条线索（说法）都是真实的，但如果我们同时检查它们，我们可以看到它们不可能都是真的。这是因为巴拉克·奥巴马在哈佛大学学习时主修法律而不是政治学。因此，如果不适当地将不同的线索/主张放在一起检查，我们可能无法发现它们之间的不一致。

为了便于比较推理，如何利用知识图中的背景信息是一个重要的问题。

如果我们能在知识图谱中找到一个子图，它能最好地表达每个输入线索的语义，那么隐藏的冲突就更容易被检测到。理想情况下，这个子图应该包含知识图中与给定线索相关的所有有意义/重要的实体和关系。我们称之为子图 知识段，其形式定义如下：

知识段（Knowledge Segment KS）

知识图谱中能够最好地表述一条线索的语义的连接子图。

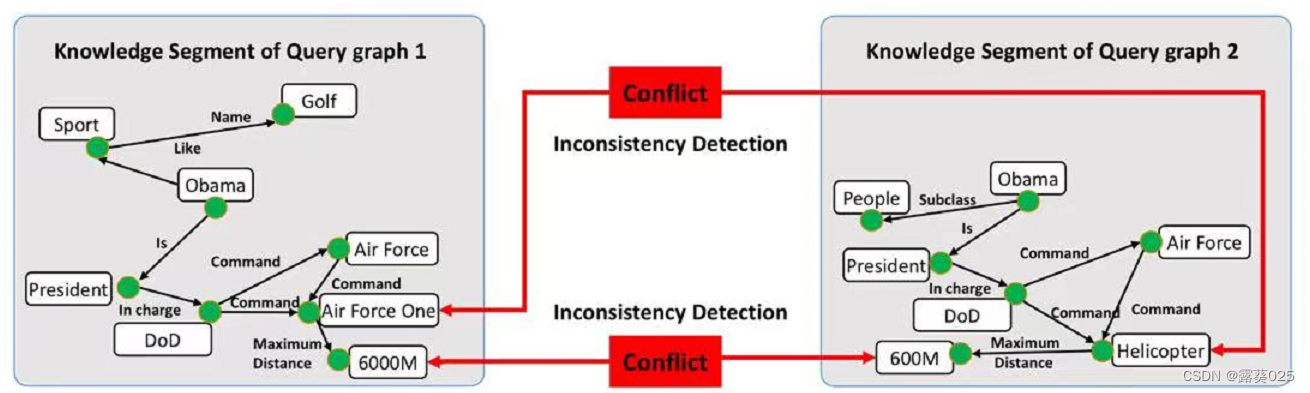
可以看到，用知识片段来表达给定的线索可以帮助我们毫不费力地发现不一致性。

对于成对的案例来说，这种共性指的是两个知识片段的相同元素。不一致性包括相互矛盾的任意元素。

共性

两个三元组的共性是指这两个三元组共享的点和边，也是两个知识片段共享的点和边。

不一致性

两个知识片段中任何相互矛盾的元素（节点、节点属性、边）

集体共性

在一个查询图中的任意三元组之间的共同点也就是集体共同性

集体不一致性

在一个查询图的所有知识片段中相互矛盾的任何元素

成对比较推理

给出一个知识图谱和两个三元组，输出关于这两个三元组一致性的二元决策

集体比较推理

给出一个知识图谱和一个查询图，输出关于查询图一致性的二元决策

知识片段提取

本节将介绍如何对抽取知识段，以最好地表达给定术语的语义。

首先介绍了如何将知识图转换为关系指定的加权图，并介绍了如何从中提取特定于边的知识段（Edge-specific KS）和特定于子图的知识段（Subgraph-specific KS）。

知识段提取的目的是抽取一个子图，该子图能够最好地表达给定线索的语义。目前已经提出了许多现有的方法来提取加权图或未加权图中从查询边的源节点到其目标节点的简明子图。

然而，这些方法并不直接适用于知识图，因为知识图的边（即谓词）具有特定的语义（如类型、关系）。为了解决这个问题，我们试图通过设计用于知识段提取的谓词-谓词相似性（Predictate-Predictate Similarity）度量，将知识图转换为加权图。

Predictate-Predictate Similarity

为了将知识图转化为加权图，我们提出使用基于TF-IDF的方法来测量不同谓词之间的相似性，并将知识图转换为一个加权图，其边缘权重表示边缘谓词和查询谓词之间的相似度。

基于TF-IDF的方法的关键思想是，将知识图中的每个三元组及其相邻的三元组视为一个文档，并使用类似TF-IDF加权策略来计算谓词相似度。例如，谓词receiveDegreeFrom可能有相邻谓词major和graditeFrom。这些谓词具有高度的相似性。

具体而言，使用知识图谱来构建一个谓词的同时发生矩阵（co-occurence maxtrix of predicates），并且通过类似TF-IDF加权策略计算他们的相似度。

对于Predictate-Predictate Similarity来说，假设我们想计算major和study的相似度。major和study都只有一个相邻谓词graduate。这意味着谓词i ≠graduate，同时发生矩阵U(major,i)=U(study,i)=0。

特定边的知识段

特定边的知识片段提取旨在找到一个知识片段来最好地表征给定边的语义上下文（即三元组）。

对于带权图，存在几种连接子图提取方法，例如，使用基于重新启动的随机行走方法来找到近似子图；使用最大网络流来寻找子图，旨在寻找更密集的局部图分区。

在本文中，将知识图转换为带权图后，我们找到了从给定查询边的主体到对象的k-simple最短路径作为其知识段。

特定子图知识段

根据特定边知识段提取的思想，我们在给定的子图中的每个边缘提取一个知识段，并将包含所有边缘特定知识片段的图称为图特定知识片段。换言之，子图特定知识段由多个相互链接的边缘特定知识段组成（即，输入查询子图的每条边缘对应一个边缘特定知识片段）。

特定子图知识段提供了更为丰富的语义，包括查询图的每条边的语义和输入查询图的不同边之间的关系的语义。

比较推理

首先介绍什么情况下我们需要对两条线索（两个边或三元组）使用成对推理，然后介绍了两种侧重于成对推理的方式。最后，我们提出了集体比较推理。这些功能背后主要思想就是，使用知识段来表达每一个查询三元组的语义，并且根据知识段中的信息检查不一致性。

成对比较推理的情景

由上述六种情况可以看出，C₁、C₅、C₆涉及的是不同的事情，因此，也就不需要检查它们之间的不一致性。
对于C₂而言，我们只需要检查它们的谓语的语义即可，比如 p₁和p₂是否矛盾。例如 p₁ = isFather ，p₂ = isSon，那么它们彼此之间就是不一致的，否则它们之间就没有不一致性。

主要看C₃和C₄，这两条线索即使它们每一个都是真的也有可能不一致。例如<奥巴马，毕业于，哈佛大学>或者<奥巴马，主修，政治科学>可能都是真的，但是把它们放在一起看，它们不可能都是真的，因为奥巴马在哈佛大学读书的时候主修的是法律，而不是政治科学。换言之，它们是相互排斥的，因此是不一致的。然而，<艾伦，出生在，迈达威尔>和<艾伦，出生在，英国>这两条就可以同时是真的，因为迈达威尔属于英国。

所以，可以看出，1. 如果两条线索的主体是相同的；2. 它们的谓词彼此相似或相同，那它们涉及的是同一件事情。

进一步，如果它们的对象是两个不相关的实体，那这两条线索大概率是不一致的。

基于以上观察，我们采取以下三个步骤进行配对比较推理。

1. 给出一对线索，通过检查这两条线索的主语、谓语和宾语，我们决定它属于六种情况中的哪一种。
2. 如果这对线索属于C3或C4，我们需要进一步判断它们是否一致。在下面的部分中，我们将说明如何处理这种情况。

基于神经网络的成对比较推理

给定一对线索中属于C3或C4的两个知识段，我们将每个知识段视为一个属性图，并采用 网络对齐（network alignment） 的一些思想来促进比较推理。
基本思想是，如果两个知识段是一致的，那么它们的大多数节点必须能够在嵌入空间中相互对齐或接近。否则，不一致节点的嵌入距离应该过大。通常，不一致性检查问题类似于嵌入空间中的异常检测或相异性检测问题。

网络对齐（Network Alignment）
指在两个或多个不同的网络之间，通过找到节点之间的对应关系，将这些网络进行对齐或匹配的过程。这个概念通常用于图论和网络科学中，用于比较和分析不同网络之间的相似性和关联性。

在对一对知识段进行推理时，我们考虑两种信息：结构信息和语义信息。
例如，空军一号和直升机具有相似的结构信息，因为它们有许多共同的邻居，但它们的语义非常不同，这可能表明这两个知识片段之间存在潜在的不一致。
另一方面，即使空军一号和直升机有不同的结构信息（在考虑 边缘类型 时），它们也有不同的语义信息。这提示它们指的是不同的事物。
受此启发，我们提出了一个 同时考虑知识片段的 结构信息 和 语义信息 的神经网络模型，以实现成对的比较搜索。

边缘类型（Edge Type）
指连接图中两个节点的边的类型或关系类型。边缘类型描述了节点之间的语义关系，用于表示实体之间的连接、属性之间的关系或其他语义关联。
边缘类型通常是通过标签或属性来表示的，可以是预定义的，也可以是根据具体应用场景定义的。不同的知识图谱可能有不同的边缘类型，例如，在一个人物关系图谱中，可能存在"父子关系"、“兄弟关系”、"朋友关系"等边缘类型。
通过定义和使用不同的边缘类型，知识图谱能够更准确地表示实体之间的关系，并支持更复杂的查询和推理操作。

为了对结构相似性进行编码，我们使用 随机游走重启(Random Walk with Restart)（考虑边缘类型）对知识片段的结构信息进行编码。

Random Walk with Restart（随机游走重启）
是一种图算法，用于在图中进行节点排序或推荐任务。它结合了随机游走和重启机制，通过模拟节点之间的随机游走来计算节点之间的相似度或相关性。
在随机游走过程中，从一个起始节点开始，根据一定的概率选择下一个节点进行扩散。重启机制会定期将游走的节点重置为起始节点，以防止游走过程过于远离起始节点。这样做可以平衡节点的局部和全局信息，使得算法能够在节点之间进行有效的传播和探索。
Random Walk with Restart常用于图中的节点排序和推荐任务。通过计算节点之间的相似度或相关性，可以将节点按照重要性进行排序，或者根据节点之间的相似性为用户进行推荐。

给定一组 锚节点（anchor node），随机游走重启将计算跟每个锚节点有关的知识段中每个节点的分数。如果两个节点具有相似的随机游走重启得分向量，则它们的结构相似性应该很高。

锚节点（Anchor Node）
是在网络对齐中使用的一种特殊节点。锚节点是两个或多个网络中 已知对应关系 的节点，它们在不同网络中具有明确的对齐关系。通过使用锚节点，可以将其他节点与其对齐，从而实现整个网络的对齐。
锚节点的选择通常基于一些先验知识或已知的相似性度量。在网络对齐算法中，通过将锚节点的对齐关系与其他节点之间的相似性进行比较，可以推断出其他节点的对齐关系。

为了对知识片段的语义信息进行编码，我们从知识图谱中抽取一些路径，并将每条路径视为一个句子，知识图中的节点可以视为句子中的单词。如果两个节点出现在同一个句子中，它们的语义信息应该相似。

结构嵌入

给定两个知识片段，这两个知识段中的公共节点可以被视为锚实体，结构嵌入旨在将知识片段中的节点嵌入到 高维空间，同时保留其结构信息。

“high dimension space”（高维空间）
指一个具有很多维度的空间。在这个空间中，每个维度都代表了知识图谱中的一个特征或属性。
在知识图谱中，每个节点可以有多个属性，每个属性可以有多个取值，这就导致了高维度的特征表示。
以一个简单的例子来说明，假设我们有一个人物关系图谱，其中包含了人物的姓名、年龄、性别、国籍等属性。将每个人物看作一个节点，每个属性看作一个维度，那么我们就可以将这个人物关系图谱表示为一个高维空间，其中每个节点在这个空间中的位置由其属性值确定（可以用不同的数值表示方法或特征提取方法来将属性值转化为节点在空间中的坐标）。

核心思想是，锚链路(Anchor Link) 集合L为两个网络中的所有节点提供了 陆标。基于锚链路的相对位置可以为所有节点形成统一的空间，而不管它们属于哪个网络。因此，我们可以使用重新启动的随机行走来测量节点和锚链接之间的相对位置。让KS₁和KS₂作为两个知识片段。
给定锚定链接l∈L（我们使用l₁和l₂来表示KS₁和KS₂中的链接实体），可以获得大小为n₁×1的RWR得分向量r l ₁

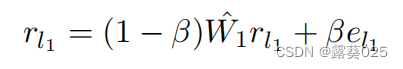
在使用锚点进行目标检测时，通常需要定义一个参考点或参考区域，称为landmark或landmark point，用于生成相对于该参考点或参考区域的锚点。这个参考点或参考区域也可以称为锚点提供的landmark。

Anchor Link
是指一个连接两个不同实体之间的关系或连接的链接，类似于超链接。这种链接通常由两部分组成：源实体和目标实体之间的关系和目标实体的标识符。
Anchor Link的作用是将不同实体之间的关系或连接可视化，以便更好地理解它们之间的联系。例如，在一个包含人物、书籍和作者的知识图谱中，可以使用Anchor Link将一个人物与他所写的所有书籍之间的关系可视化，或将一本书与它的作者之间的关系可视化。
Anchor Link在知识图谱中也可以用于支持实体之间的跳转和导航，类似于网页上的锚点链接。用户可以通过单击Anchor Link，快速跳转到与当前实体相关联的其他实体，以便深入研究和探索知识图谱中的关系和连接。

语义嵌入

为了理解知识段中每个节点的语义，我们在背景知识图谱中随机抽取一些路径，并将每条路径视为句子，而将每个节点视为句子中的一个单词。然后我们使用流行的语言模型Bert来学习每个节点的语义嵌入。如果两个节点出现在同一路径上，则它们的语义嵌入应该彼此靠近，反之，它们的语义嵌应该彼此远离。

我们将两个知识段的节点语义嵌入和结构嵌入连接起来，并使用图神经网络分别学习KS₁和KS₂的图嵌入。最后根据图的嵌入来预测它们是否一致。该算法的体系结构如图所示

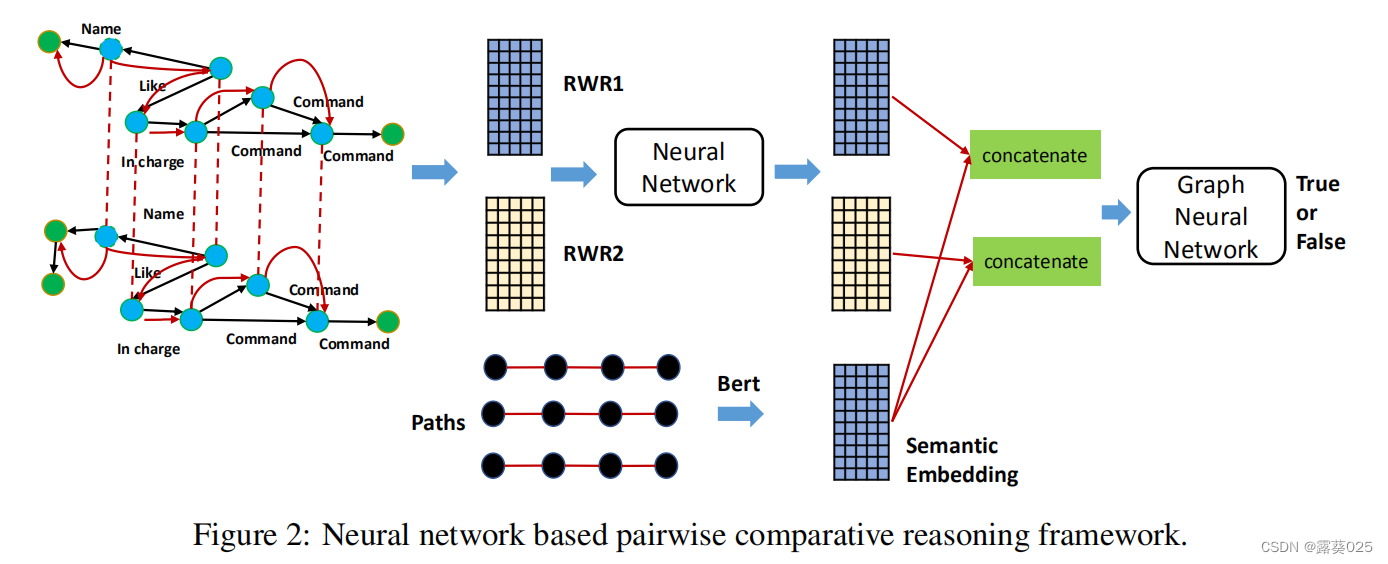
GNN图神经网络的定义：

伪代码：

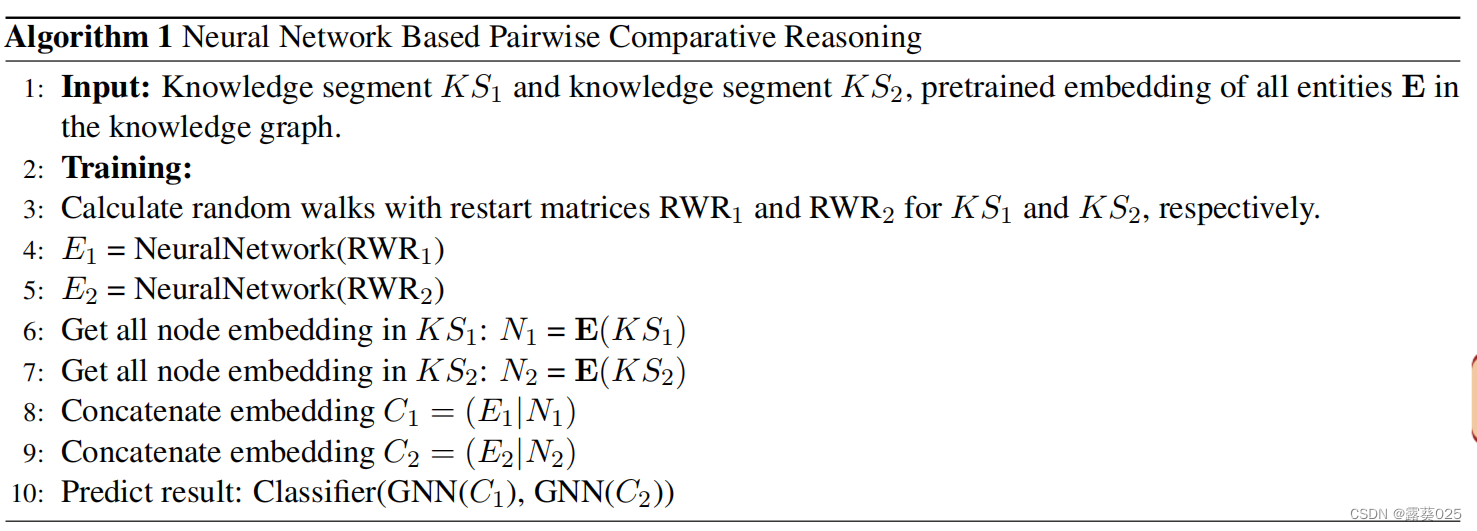
基于图核的成对比较推理

与基于神经网络的成对比较推理不同，基于图核的成对比较推理旨在利用图核在这两个知识段中找到一组关键元素（节点或边或节点属性）， 然后根据这些元素和知识图谱中的相关信息做出决策。其想法是，如果这些关键元素中的大多数都属于这两个知识片段的共性，那么它们很可能指的是同一件事。否则，这两条线索指的是不同的东西。第三，如果它们指的是同一件事，我们将进一步决定它们是否相互冲突。在这里，关键思想如下。我们构建了两个新的查询三元组<O₁，isTypeof，O₂>和<O₂，isTypeof，O₁>。如果其中一个个为真，那么原来的两个三元组是一致的。否则，它们是不一致的。

为了找到关键元素，我们建议使用关于知识分段相似性的影响函数。
基本思想是，如果我们扰乱关键元素（例如，更改节点的属性或删除一个节点或边），这将对这两个知识段之间的总体相似性产生显著影响。我们可以将知识段视为属性图，其中不同的实体具有不同的属性。我们使用具有节点属性的随机游走图核来测量这两个知识片段之间的相似性。

我们提出使用关于知识段元素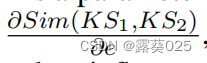 的影响函数Sim(KS₁, KS₂)，其中e代表一个KS₁ 或KS₂中的元素。具有高绝对影响函数值的元素被视为关键元素，它可以是节点、边或节点属性。不同元素的影响函数可以根据以下引理计算。

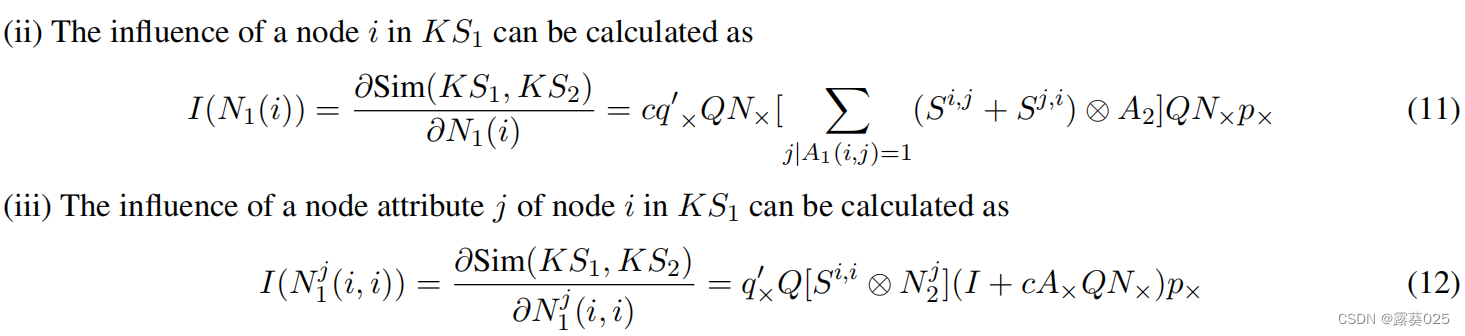
对于给定的知识片段，我们将具有最高绝对影响函数值的前50%的元素（例如，节点属性、节点和边缘）标记为关键元素。
我们想检查一下这些关键元素是否属于这两个知识段的共性。如果它们中的大多数（例如，60%或更多）属于这两个知识片段的共性，我们就说这两个查询线索描述的是同一个东西。否则，它们指的是不同的东西，因此我们不需要检查它们之间的不一致性。
如果我们确定查询线索指的是相同的东西，下一步就是判断它们是否不一致。也就是说，给定查询线索<s1，p1，o1>和<s1，p2，o2>，我们需要确定o1属于o2还是o2属于o1。为此，我们构建了两个新的查询<o1，isTypeof，o2>和<o2，isTypeof，o1>。然后，我们提取这两个查询的知识片段，并检查这两个片段是否为真。如果其中一条是真的，我们就说原始线索是一致的，否则就是不一致的。在我们提取<o1，isTypeof，o2>和<o2，isTypeof，o1>的知识片段后，我们将每个知识片段视为有向图，并计算有多少信息可以从主体传递到对象。我们将转移的信息量定义为：

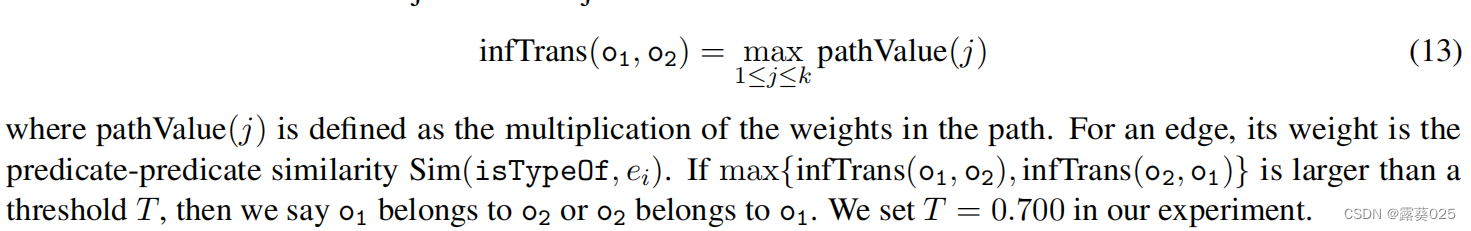
基于图核的集体比较推理

与成对比较推理不同，集体比较推理 旨在发现由一组互连边（三元组）组成的查询图内部的共性和（或）不一致性。
对于前者（成对比较推理），如果两条线索（例如新闻文章中的两条声明）在查询图上较弱或不相关，我们可能根本不需要检查它们之间的不一致性。
对于后者（集体比较推理），在一些副标题中，只有当我们对多个（两个以上）知识片段进行集体推理时，才能识别出语义不一致。例如，考虑到以下三种说法，包括（1）奥巴马被空军一号拒绝；（2） 奥巴马是美国总统；（3） 美国总统在一架直升机前。只有我们把这三种说法放在一起推理，我们才能发现它们之间的语义不一致。

基于上述观察，我们提出了下面的方法来发现集体不一致性。

首先，我们在语义匹配子图中找到一组关键元素。与成对比较推理不同，一个元素对集体比较推理的影响是由整个语义匹配子图来计算的。更具体地说，我们首先将查询图及其语义匹配子图（即子图特定知识段）转换为两个线形图，定义如下。
线形图：对于任意图G=（V,E），G的线形图L（G）=（V^’，G^’）有以下属性：

1. L(G)的节点集是G（V^’ = E）的边集
2. 当且仅当对应G的边e_i、e_j入射在G中的同一节点上时，L(G)的两个节点V^’_i，V^’_j是相连的。
   
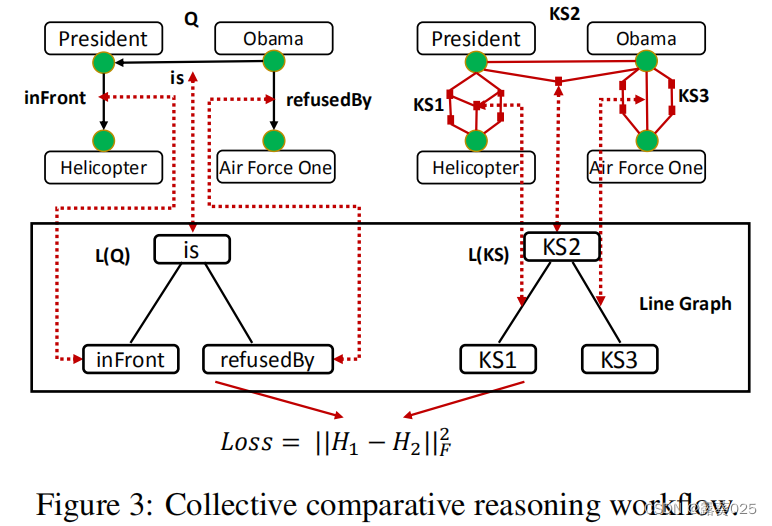
   图3给出了一个线形图的例子。对于线形图L(Q) ，边的权重是它所连接的两个节点的谓词-谓词相似性。对于线形图L(KS)，边的权重是它连接的两个节点的知识段相似度。构建这两个折线图的合理性在于，如果语义匹配子图是原始查询图的良好表示，则L(Q) 中的边缘相似度将类似于L(KS) 中的知识段相似性。

为了测量一个元素的重要性，我们提出使用关于L(Q)和L(KS)的距离的影响函数。我们假设一个关键元素被改变，这将会对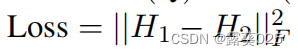距离产生大影响，其中H₁是L(Q)的加权连接矩阵，H₂是L(KS)的加权连接矩阵。
我们使用影响函数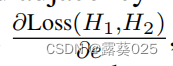，其中e是知识段中的一个元素。下面提供了如何计算影响函数的细节。


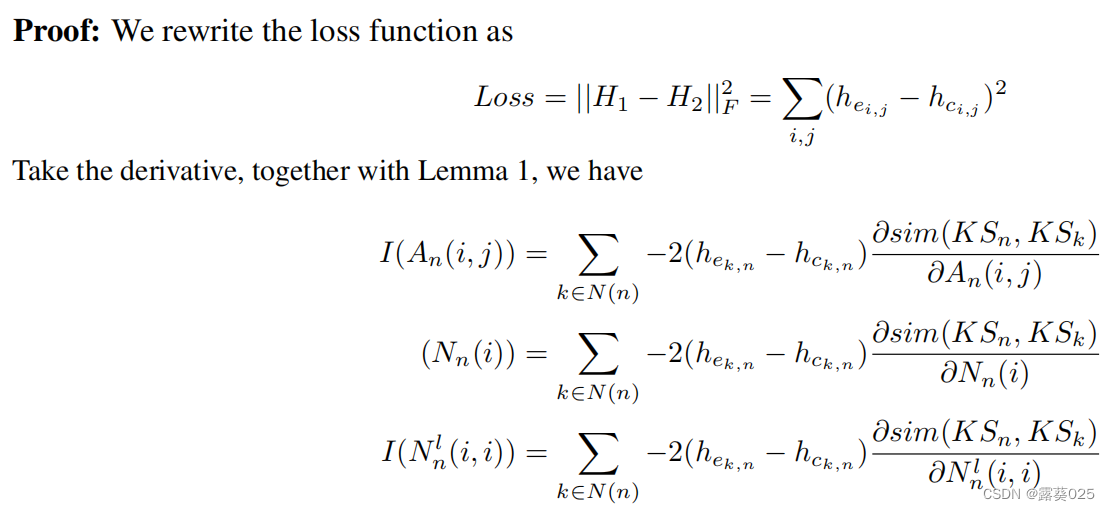
其次，在找到所有关键元素后，根据这些关键元素检查语义匹配子图的一致性。步骤如下：

对于语义匹配子图的每对知识段，如果它们的关键元素重叠率大于阈值（60%），我们检查这对知识段的一致性。假设相应的三元组分别为<s1，p1，o1>和<s2，p2，o2>。我们检查<s1，isTypeof，s2>或<s2，isTypeof，s1>是否为true。如果它们都是假的，我们跳过这对线索，因为它不属于C3或C4。
否则，我们检查<o1，isTypeof，o2>或<o2，isTypeof，o1>是否为true。如果两者都为false，则表示该查询图具有集体不一致性。当检查三元组（例如，＜s1，isTypeof，s2>，＜s2，isTypeof，s1>，＜o1，isTypeof，o2>和＜o2，isTypeof，o1>）的真实性时，我们使用与成对比较推理相同的方法（即，方程中的传递信息量）。