欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
参考自polygon mesh proccessing这本书
基本思路及原理
余切拉普拉斯算子是一种考虑了网格底层几何联系的一种算子,在网格平滑,参数化等算法中经常被用到。它是受到了有限元思绪启发推导出来的。
用到有限元中的散度定理。
目标是对三角平面分片线性函数的梯度的散度进行面积积分。
散度定理如下,对散度的面积分,可以转化为梯度对边界的线积分。
∫
A
i
d
i
v
F
(
u
)
d
A
=
∫
∂
A
i
F
(
u
)
⋅
n
(
u
)
d
s
\int_{A_i}div\;F(u)\operatorname dA = \int_{\partial A_i}F(u) \cdot n(u) \operatorname ds
∫AidivF(u)dA=∫∂AiF(u)⋅n(u)ds
上述式子把对 A i 面积的积分和对 A i 边界( ∂ A i )的积分联系起来。 其中 n 代表与三角形共面并垂直于边界向外的单位向量。 上述式子把对A_i面积的积分和对A_i边界(\partial A_i)的积分联系起来。\\其中 \boldsymbol n 代表与三角形共面并垂直于边界向外的单位向量。 上述式子把对Ai面积的积分和对Ai边界(∂Ai)的积分联系起来。其中n代表与三角形共面并垂直于边界向外的单位向量。
拉普拉斯积分推导
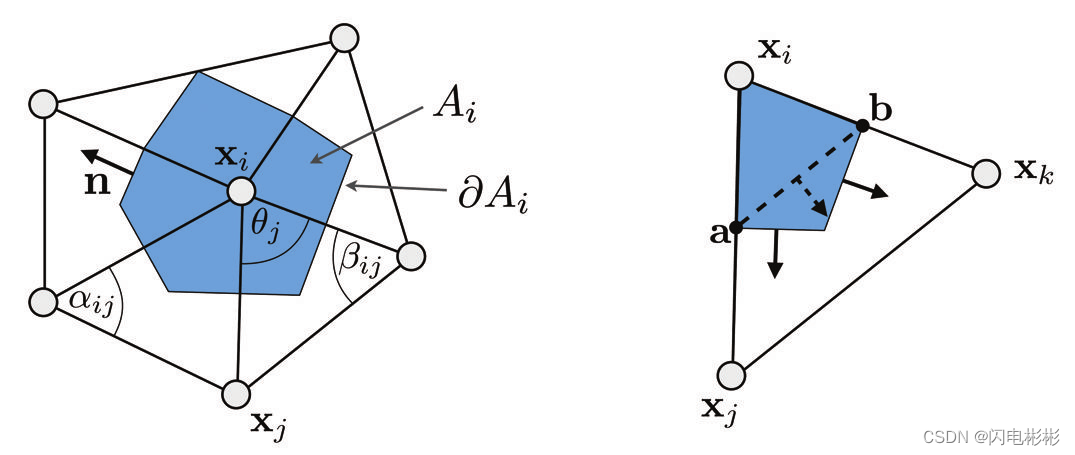
将上述定理应用于拉普拉斯,可以得到下述公式
∫ A i Δ f ( u ) d A = ∫ A i d i v ∇ f ( u ) d A = ∫ ∂ A i ∇ f ( u ) ⋅ n ( u ) d s \int_{A_i}{\Delta f(\boldsymbol u) \operatorname d A} = \int_{A_i}{div \nabla f(\boldsymbol u) \operatorname dA} =\int_{\partial A_i}{\nabla f(\boldsymbol u) \cdot \boldsymbol {n(u)} \operatorname d s} ∫AiΔf(u)dA=∫Aidiv∇f(u)dA=∫∂Ai∇f(u)⋅n(u)ds
我们可以对每个三角内的区域进行积分,如上图的右图,对于单个三角形,积分如下,三角形的梯度是常量可以提出来,a和b是中点。
∫ ∂ A i ∩ T ∇ f ( u ) ⋅ n ( u ) d s = ∇ f ( u ) ⋅ ∫ ∂ A i ∩ T n ( u ) d s = ∇ f ( u ) ⋅ ( a − b ) ⊥ = 1 2 ∇ f ( u ) ⋅ ( x j − x k ) ⊥ \int_{\partial A_i \cap T}{\nabla f(\boldsymbol u) \cdot \boldsymbol {n(u)} \operatorname d s} = \nabla f(\boldsymbol u) \cdot \int_{\partial A_i \cap T}{\boldsymbol {n(u)} \operatorname d s}= \nabla f(\boldsymbol u) \cdot (\boldsymbol a-\boldsymbol b)^\perp\\ =\frac 1 2 \nabla f(\boldsymbol u) \cdot (\boldsymbol {x_j}-\boldsymbol {x_k})^\perp ∫∂Ai∩T∇f(u)⋅n(u)ds=∇f(u)⋅∫∂Ai∩Tn(u)ds=∇f(u)⋅(a−b)⊥=21∇f(u)⋅(xj−xk)⊥
下面解释一下上式中(a-b)怎么来的。
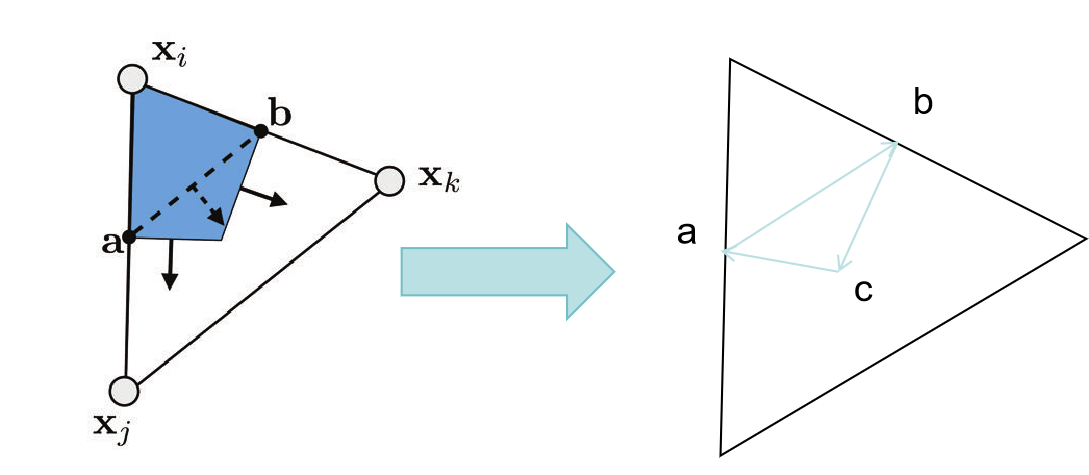
我们先把线的法向转90度与中间的小三角形平齐。
对线的积分就是乘上线的长度,所以旋转以后的分积就是小三角形三条边形成的向量。
原来积分的结果应该是
(a-c)+(c-b)
由于(a-c)+(c-b)+(b-a)=0
所以(a-b) = (a-c)+(c-b)
转化成余切形式
三角形的梯度是一个常量,代入上式,得到
∫ ∂ A i ∩ T ∇ f ( u ) ⋅ n ( u ) d s = ( f j − f i ) ( x i − x k ) ⊥ ⋅ ( x j − x k ) ⊥ 4 A T + ( f k − f i ) ( x j − x i ) ⊥ ⋅ ( x j − x k ) ⊥ 4 A T \int_{\partial A_i \cap T}{\nabla f(\boldsymbol u) \cdot \boldsymbol {n(u)} \operatorname d s} = (f_j-f_i)\frac {(x_i-x_k)^\perp \cdot (x_j-x_k)^\perp}{4A_T} + (f_k-f_i)\frac {(x_j-x_i)^\perp \cdot (x_j-x_k)^\perp}{4A_T} ∫∂Ai∩T∇f(u)⋅n(u)ds=(fj−fi)4AT(xi−xk)⊥⋅(xj−xk)⊥+(fk−fi)4AT(xj−xi)⊥⋅(xj−xk)⊥
向量的点乘和叉乘可以转化成余弦和正弦。
γ j , γ k 表示 v j , v k 点上对应的角 \gamma_j,\gamma_k表示 v_j, v_k 点上对应的角 γj,γk表示vj,vk点上对应的角
面积
A
T
=
1
2
s
i
n
γ
j
∥
x
j
−
x
i
∥
∥
x
j
−
x
k
∥
=
1
2
s
i
n
γ
k
∥
x
i
−
x
k
∥
∥
x
j
−
x
k
∥
A_T=\frac {1} {2} sin \gamma_j\left\|x_j-x_i\right\|\left\|x_j-x_k\right\|=\frac {1} {2} sin \gamma_k\left\|x_i-x_k\right\|\left\|x_j-x_k\right\|
AT=21sinγj∥xj−xi∥∥xj−xk∥=21sinγk∥xi−xk∥∥xj−xk∥
点乘
c
o
s
γ
j
=
(
x
j
−
x
i
)
⋅
(
x
j
−
x
k
)
∥
x
j
−
x
i
∥
∥
x
j
−
x
k
∥
cos \gamma_j = \frac {(x_j-x_i)\cdot(x_j-x_k)}{\left\|x_j-x_i\right\|\left\|x_j-x_k\right\|}
cosγj=∥xj−xi∥∥xj−xk∥(xj−xi)⋅(xj−xk)
c o s γ k = ( x i − x k ) ⋅ ( x j − x k ) ∥ x i − x k ∥ ∥ x j − x k ∥ cos \gamma_k = \frac {(x_i-x_k)\cdot(x_j-x_k)}{\left\|x_i-x_k\right\|\left\|x_j-x_k\right\|} cosγk=∥xi−xk∥∥xj−xk∥(xi−xk)⋅(xj−xk)
将上面公式代入式子可得到
∫ ∂ A i ∩ T ∇ f ( u ) ⋅ n ( u ) d s = 1 2 ( c o t γ k ( f j − f i ) + c o t γ j ( f k − f i ) ) \int_{\partial A_i \cap T}{\nabla f(\boldsymbol u) \cdot \boldsymbol {n(u)} \operatorname d s} = \frac 1 2 (cot \gamma_k(f_j-f_i)+cot \gamma_j(f_k-f_i)) ∫∂Ai∩T∇f(u)⋅n(u)ds=21(cotγk(fj−fi)+cotγj(fk−fi))
上面公式是对一个三角形内区域的积分。
把所有三角形各分加起来,可以发现每条边都对应两个角(看最上面那张图左边),整体公式如下。
∫ A i Δ f ( u ) d A = 1 2 [ ∑ v j ∈ N ( v i ) ( c o t α i , j + c o t β i , j ) ( f j − f i ) ] \int_{A_i}{\Delta f(\boldsymbol u) \operatorname d A} = \frac 1 2 \left [\displaystyle \sum_{v_j\in N(v_i)}(cot \alpha_{i,j}+cot \beta_{i,j})(f_j-f_i)\right ] ∫AiΔf(u)dA=21 vj∈N(vi)∑(cotαi,j+cotβi,j)(fj−fi)
得到点的拉普拉斯公式如下
Δ f ( v i ) = 1 2 A i [ ∑ v j ∈ N ( v i ) ( c o t α i , j + c o t β i , j ) ( f j − f i ) ] \Delta f(v_i) = \frac {1} {2A_i} \left [\displaystyle \sum_{v_j\in N(v_i)}(cot \alpha_{i,j}+cot \beta_{i,j})(f_j-f_i)\right ] Δf(vi)=2Ai1 vj∈N(vi)∑(cotαi,j+cotβi,j)(fj−fi)
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。



![[SSM]Spring中的JdbcTemplate](https://img-blog.csdnimg.cn/feb255d32aee4bc98a20af59da798062.png)