Honda, Hiroto, and Yusuke Uchida. “CLRerNet: Improving Confidence of Lane Detection with LaneIoU.” arXiv preprint arXiv:2305.08366 (2023).
2023.05 出的一篇车道线检测的文章, 效果在CULane, CurveLanes SOTA
文章目录
- 简介
- LaneIoU
- LineIoU存在问题
- 为什么使用LaneIoU
简介
这篇论文在CLRNet基础上, 使用提出的LaneIoU代替CLRNet论文中LineIoU, 在两个数据集上取得了SOTA效果
LaneIoU
论文其他部分可以不看, 直接调到3.2 LaneIoU即可;
LineIoU存在问题
从下面图片及公式(CLRNet)可发现, 当车道线越水平时, 通过该公式计算出来的IoU越大, 比如从两侧出发的车道线, 预测线和GT离得很近, 但是使用该LineIoU计算得到较大的值, 导致在分配正负样本和计算loss时候均带来副作用, 导致模型效果不佳;
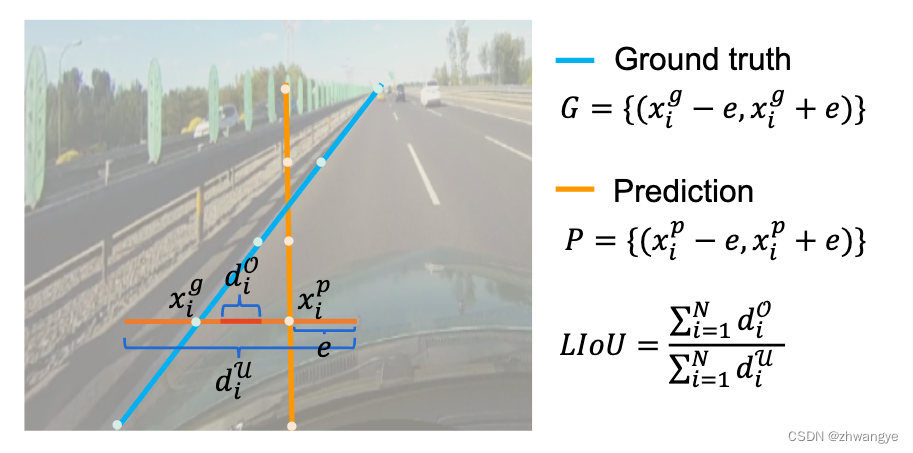
注意: 这里的e是一个常数, CLRNet中取得为15
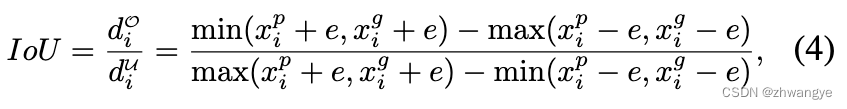
为什么使用LaneIoU
为了解决LineIoU存在的问题, 如上,
从下图可发现, 公式3,4 和 CLRNet公式4 很相似, 仅仅把 e e e换成了 w w w, 从一个固定值变成动态计算, 主要计算由公式7给出,