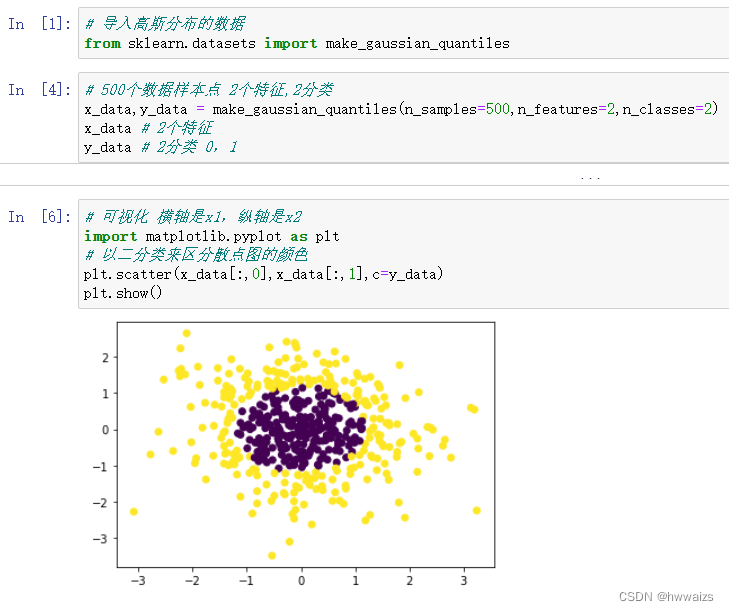
线性回归所解决的问题是把数据集的特征传入到模型中,预测一个值使得误差最小,预测值无限接近于真实值。比如把房子的其他特征传入到模型中,预测出房价, 房价是一系列连续的数值,线性回归解决的是有监督的学习。有很多场景预测出来的结果不一定是连续的,我们要解决的问题并不是一直类似于房价的问题。
分类问题
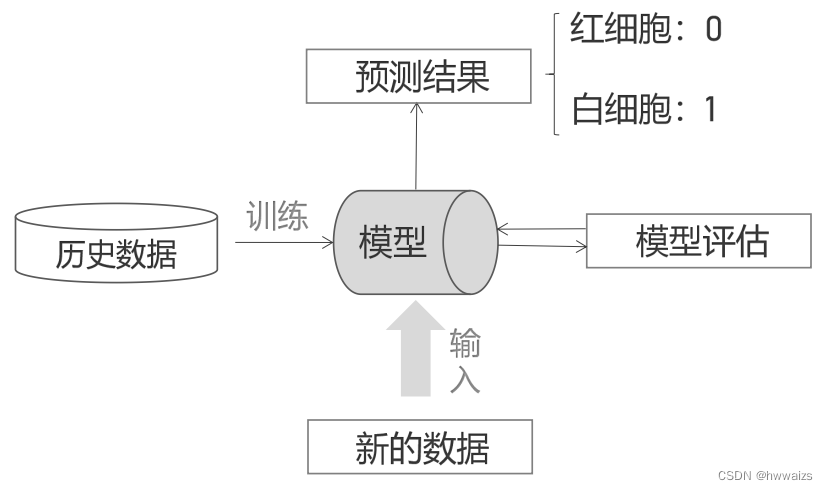
预测是红细胞还是白细胞,红细胞和白细胞是两个完全不同的类别。预测的时候首先要有历史数据,训练出模型,然后对模型进行反复的评估后得到理想的模型,然后把新的数据传入到模型中,进行一系列的预测,得到是红细胞(0),或者白细胞(1),这是最简单的二分类的问题。
如果用线性回归解决分类问题,
y
=
0
y=0
y=0为红细胞,
y
=
1
y=1
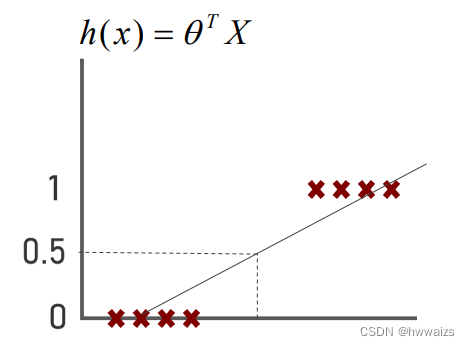
y=1为白细胞,数据集的呈现情况如下图所示,此时需要找到一条线,把二者分开,用线性回归去做的话,一要考虑代价函数最小(误差最小),二要将数据最好的分开。要将红白细胞分开的话,在线上取一个值(0.5),若
h
(
x
)
>
=
0.5
h(x)>=0.5
h(x)>=0.5的话,得到的点在上方,预测的结果为1;如果
h
(
x
)
<
0.5
h(x)<0.5
h(x)<0.5的话,得到的点在下方,预测的结果为0。
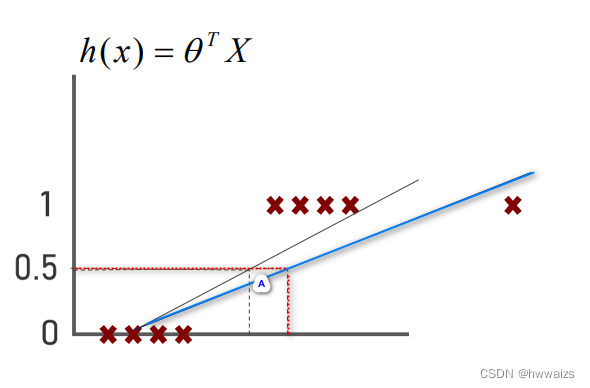
如果数据中多了一个样本点,如下图所示,拟合线的求解应该是代价函数最小,拟合线会出现往右侧拓展的情况,为图中蓝色的线,如果
h
(
x
)
=
0.5
h(x)=0.5
h(x)=0.5的话,会出现在A区域的点不是完全为1的。也就是说当数据中出现了一个异常的样本点的时候,用线性回归模型解决问题的时候,就会让我们整体的预测都发生变化,这时就要引入逻辑回归算法。
逻辑回归
逻辑回归算法是当今最流行以及使用最广泛的算法之一。虽然它的名字中含有回归二字,但实际上是用来解决分类问题的。常用的场景:数据挖掘;疾病自动诊断;经济预测领域,还有垃圾邮件分类等。逻辑回归在深度学习中也是比较重要的,它是个比较经典的算法,它的很多原理被用在深度学习、神经网络中。
逻辑回归的实现
预测函数:
h
(
x
)
=
θ
T
X
h(x)=θ^TX
h(x)=θTX,预测值会远远大于1,或远远小于0,就无法做分类,目标:将
h
(
x
)
h(x)
h(x)进行收敛到0和1之间,
0
<
=
h
(
x
)
0
<
=
1
0<=h(x)0<=1
0<=h(x)0<=1。
实现:使用
s
i
g
m
o
i
d
(
L
o
g
i
s
t
i
c
)
sigmoid(Logistic)
sigmoid(Logistic)函数,
g
(
z
)
=
1
1
+
e
−
z
g(z)=\frac{1}{1+e^{-z}}
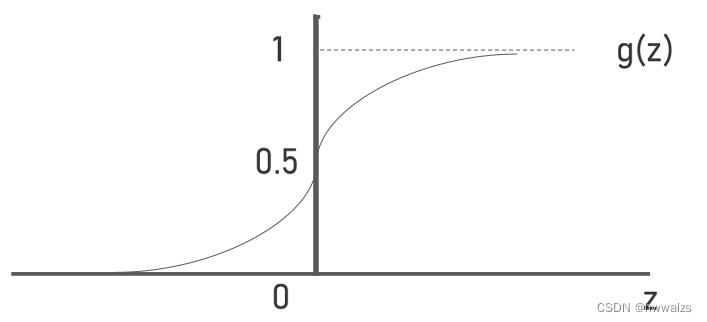
g(z)=1+e−z1。当
z
z
z趋向于
+
∞
+∞
+∞,
e
−
z
e^{-z}
e−z趋向于0,
g
(
z
)
g(z)
g(z)就无限趋向于1;当
z
z
z趋向于
−
∞
-∞
−∞,
e
−
z
e^{-z}
e−z趋向于
+
∞
+∞
+∞,
g
(
z
)
g(z)
g(z)就无限趋向于0。
把
h
(
x
)
h(x)
h(x)代入到
g
(
z
)
g(z)
g(z)中去,得到
g
(
θ
T
X
)
=
1
1
+
e
−
θ
T
X
g(θ^TX)=\frac{1}{1+e^{-θ^TX}}
g(θTX)=1+e−θTX1,可以将
g
(
θ
T
X
)
g(θ^TX)
g(θTX)映射到0和1之间。
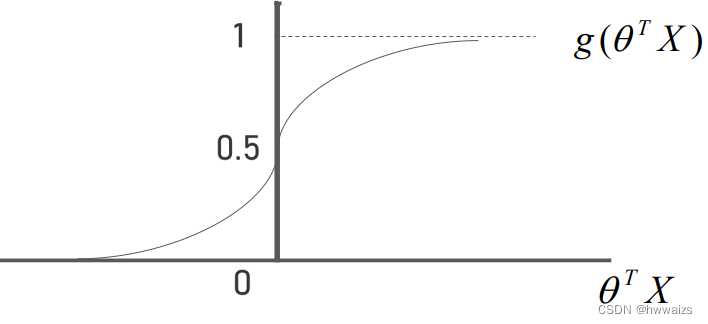
当
θ
T
X
>
=
0
θ^TX>=0
θTX>=0的时候,
g
(
θ
T
X
)
>
=
0.5
g(θ^TX)>=0.5
g(θTX)>=0.5,趋近于1;
当
θ
T
X
<
0
θ^TX<0
θTX<0的时候,
g
(
θ
T
X
)
<
0.5
g(θ^TX)<0.5
g(θTX)<0.5,趋近于0。公式还可以写为
h
(
x
)
=
1
1
+
e
−
θ
T
X
h(x)=\frac{1}{1+e^{-θ^TX}}
h(x)=1+e−θTX1。
将一组数据训练出来模型,将新的数据代入到模型中,得到预测的结果,结果不可能刚好是0或者1,也可能在0和1之间,若得到的结果
h
(
x
)
=
0.7
h(x)=0.7
h(x)=0.7,可以预测有70%的几率为白细胞(1),为红细胞(0)的概率为30%。为其中一种的概率:
h
(
x
)
=
P
(
y
=
1
∣
x
;
θ
)
h(x)=P(y=1|x;θ)
h(x)=P(y=1∣x;θ),在
y
=
1
y=1
y=1的条件下
x
x
x的概率;两者之间的概率和:
P
(
y
=
1
∣
x
;
θ
)
+
P
(
y
=
0
∣
x
;
θ
)
=
1
P(y=1|x;θ)+P(y=0|x;θ)=1
P(y=1∣x;θ)+P(y=0∣x;θ)=1。
- 总结
h ( x ) h(x) h(x)使用 g ( θ T X ) g(θ^TX) g(θTX)收敛到0和1之间。
h ( x ) = g ( θ T X ) = P ( y = 1 ∣ x ; θ ) h(x)=g(θ^TX)=P(y=1|x;θ) h(x)=g(θTX)=P(y=1∣x;θ), g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,
当 θ T X > 0 , h ( x ) > = 0.5 θ^TX>0,h(x)>=0.5 θTX>0,h(x)>=0.5,则预测 y = 1 y=1 y=1;
当 θ T X < 0 , h ( x ) < 0.5 θ^TX<0,h(x)<0.5 θTX<0,h(x)<0.5,则预测 y = 0 y=0 y=0
决策边界
帮助我们更好的理解逻辑回归,理解函数表达的内涵,
x
1
x_1
x1,
x
2
x_2
x2分布代表特征,得到
h
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
)
h(x)=g(θ_0+θ_1x_1+θ_2x_2)
h(x)=g(θ0+θ1x1+θ2x2),后半部分相当于
θ
T
X
θ^TX
θTX。
如下图所示,假设
θ
0
=
−
3
,
θ
1
=
1
,
θ
2
=
1
θ_0=-3,θ_1=1,θ_2=1
θ0=−3,θ1=1,θ2=1,得到
θ
T
X
=
−
3
+
x
1
+
x
2
θ^TX=-3+x_1+x_2
θTX=−3+x1+x2,如果
−
3
+
x
1
+
x
2
>
=
0
-3+x_1+x_2>=0
−3+x1+x2>=0,意味着
h
(
x
)
>
=
0.5
h(x)>=0.5
h(x)>=0.5,值更加接近于1,则
y
=
1
y=1
y=1划分为1的可能性比较大;如果
−
3
+
x
1
+
x
2
<
0
-3+x_1+x_2<0
−3+x1+x2<0,意味着
h
(
x
)
<
0.5
h(x)<0.5
h(x)<0.5,值更加接近于0,则
y
=
0
y=0
y=0划分为0的可能性比较大。根据表达式画线,将
−
3
-3
−3移到等号的右边,当
x
1
=
0
x_1=0
x1=0时,
x
2
=
3
x_2=3
x2=3;当
x
2
=
0
x_2=0
x2=0时,
x
1
=
3
x_1=3
x1=3,两点之间画线,在线上方是
x
1
+
x
2
>
=
3
x_1+x_2>=3
x1+x2>=3的部分,类别预测为1,同理可得,在线下方,类别预测为0。
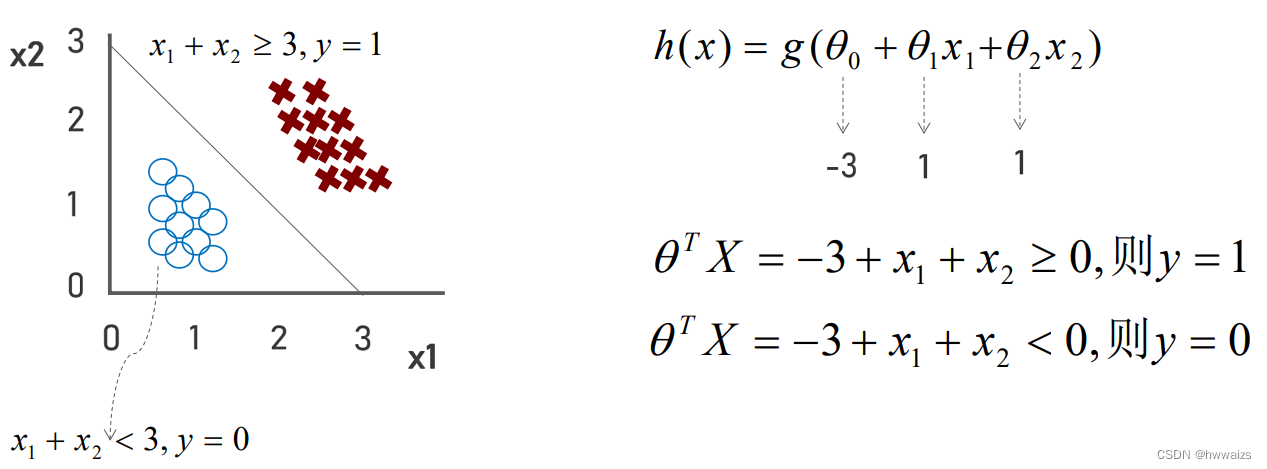
在下图中,用叉号表示正样本,用圈表示负样本,此时不能用一条直线将二者进行划分了,在之前线性回归的时候,如果数据不能用一条直线拟合,用多项式回归,添加一些高阶的式子。在逻辑回归的时候,也可以使用相同的方法。
h
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
+
θ
4
x
2
2
)
h(x)=g(θ_0+θ_1x_1+θ_2x_2+θ_3x_1^2+θ_4x_2^2)
h(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22),其中
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
+
θ
4
x
2
2
θ_0+θ_1x_1+θ_2x_2+θ_3x_1^2+θ_4x_2^2
θ0+θ1x1+θ2x2+θ3x12+θ4x22相当于
θ
T
X
θ^TX
θTX。
如下图所示,假设
θ
0
=
−
1
,
θ
1
=
0
,
θ
2
=
0
,
θ
3
=
1
,
θ
4
=
1
θ_0=-1,θ_1=0,θ_2=0,θ_3=1,θ_4=1
θ0=−1,θ1=0,θ2=0,θ3=1,θ4=1,代入公式后得到
θ
T
X
=
−
1
+
x
1
2
+
x
2
2
θ^TX=-1+x_1^2+x_2^2
θTX=−1+x12+x22,若
−
1
+
x
1
2
+
x
2
2
>
=
0
-1+x_1^2+x_2^2>=0
−1+x12+x22>=0,则可以得到
θ
T
X
=
x
1
2
+
x
2
2
>
=
1
θ^TX=x_1^2+x_2^2>=1
θTX=x12+x22>=1,
h
(
x
)
h(x)
h(x)的值大于0.5,类别划分为1,否则类别划分为0。
x
1
2
+
x
2
2
=
1
x_1^2+x_2^2=1
x12+x22=1是以原点为圆心,半径为1的标准圆,也即是决策边界,在圆外部的点是要大于半径的,属于类别为1的,反之在圆内部的点是小于半径的,属于类别为0的。决策边界是通过
θ
θ
θ来确定的,
h
(
x
)
=
1
1
+
e
−
θ
T
X
h(x)=\frac{1}{1+e^{-θ^TX}}
h(x)=1+e−θTX1,1和e都是常数,X为数据样本集(特征),只有
θ
θ
θ是个参数,只要确定了
θ
θ
θ也就确定了决策边界
h
(
x
)
h(x)
h(x),也就可以预测边界
h
(
x
)
h(x)
h(x)的值。
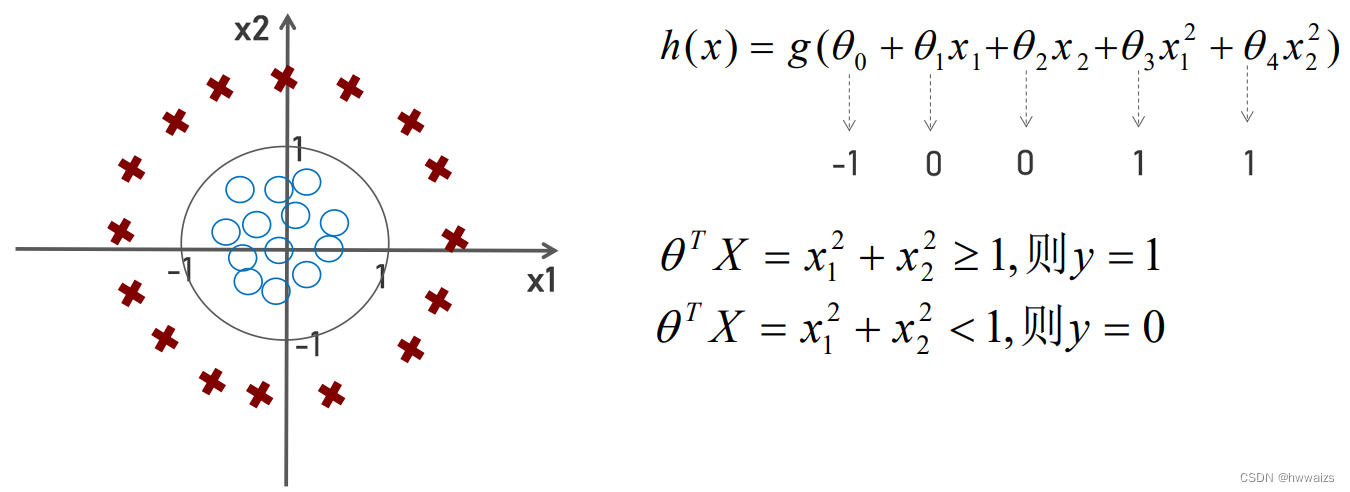
求解
θ
θ
θ值,跟线性回归有类似之处,求
θ
θ
θ是基于代价函数的,使得代价函数最小,求得
θ
θ
θ值。
代价函数
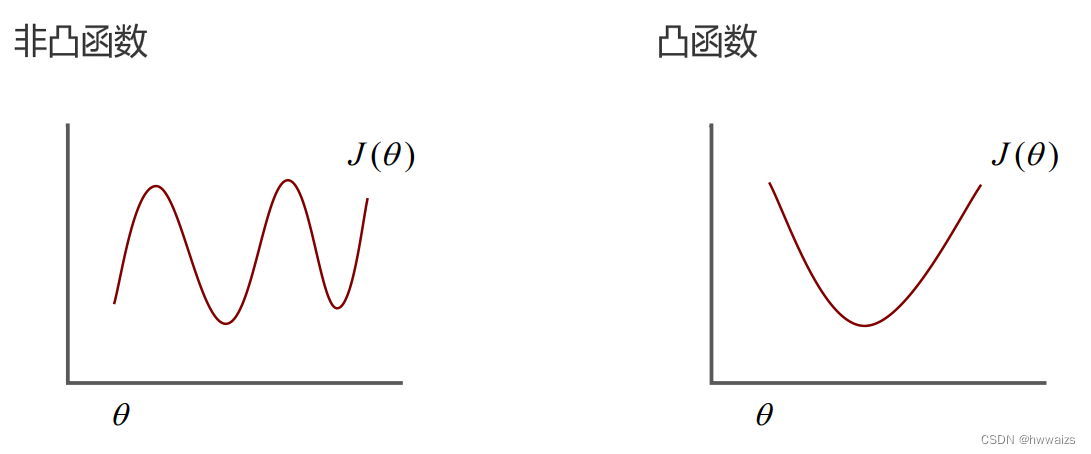
凸函数只有1个全局最优解,非凸函数求最优解的时候,很有可能陷入到局部最优解中,而不是全局最小值。非凸函数无法通过梯度下降法取得全局最小值。
线性回归所定义的代价函数为:
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
h
(
x
i
)
−
y
i
)
2
J(θ)= \frac{1}{2m}\displaystyle{\sum_{i=1}^{m}(h(x^i)-y^i)^2}
J(θ)=2m1i=1∑m(h(xi)−yi)2,真实值减去预测值的平方求和,然后除以特征的个数,也就是均方误差,此时
h
(
x
i
)
=
θ
0
+
θ
1
x
i
h(x^i)=θ_0+θ_1x^i
h(xi)=θ0+θ1xi,如果把代价函数运用到逻辑回归当中,此时
h
(
x
i
)
h(x^i)
h(xi)不再是简单的线性回归关系,而是
h
(
x
)
=
1
1
+
e
−
θ
T
X
h(x)=\frac{1}{1+e^{-θ^TX}}
h(x)=1+e−θTX1,把等号后面的内容整体代入到代价函数中去,图形就会变成非凸函数,不便于求全局最小值。
目标:找到一个不同的代价函数,能使得
J
(
θ
)
J(θ)
J(θ)变为凸函数。
实现:使用对数去掉指数化带来的影响,转化为线性关系,用对数把指数对冲掉。
2
n
=
4
2^n=4
2n=4,可以转换为
l
o
g
2
4
=
n
log_24=n
log24=n,求得
n
=
2
n=2
n=2。
解决方法:转为凸函数,如果为一元,直接求二阶导,若大于等于零,则为凸函数;如果为多元的,借助hessian矩阵来解决,涉及到正定性。
作用:凸函数的局部最优解就是全局最优解。
- 当
y
=
1
y=1
y=1时,代价函数
C
o
s
t
(
h
(
x
)
,
y
)
=
−
l
o
g
e
(
h
(
x
)
)
Cost(h(x),y)=-log_e(h(x))
Cost(h(x),y)=−loge(h(x))
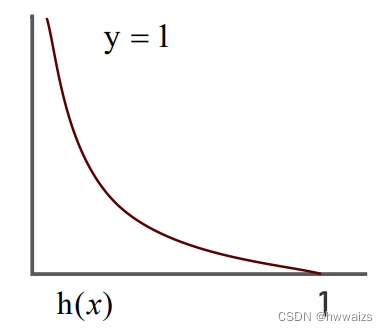
C o s t Cost Cost为当前样本预测的损失。P为概率, y = 1 y=1 y=1的概率。
当 y = 1 y=1 y=1时, h ( x ) h(x) h(x)要接近于1才能使得代价函数最小, y y y为真实值,类别为1, h ( x ) = P ( y = 1 ∣ x ; θ ) h(x)=P(y=1|x;θ) h(x)=P(y=1∣x;θ)为预测值为1的概率,概率越大就意味着越接近于结果 y = 1 y=1 y=1。如果 h ( x ) = 1 h(x)=1 h(x)=1是最好的效果, C o s t = − l o g e ( h ( x ) ) = 0 Cost=-log_e(h(x))=0 Cost=−loge(h(x))=0,意味着损失最小,代价函数为0;
如果 h ( x ) = 0 h(x)=0 h(x)=0, h ( x ) = P ( y = 1 ∣ x ; θ ) h(x)=P(y=1|x;θ) h(x)=P(y=1∣x;θ)为预测值为1的概率为0, C o s t ( h ( x ) , y ) = − l o g e ( h ( x ) ) Cost(h(x),y)=-log_e(h(x)) Cost(h(x),y)=−loge(h(x))为无穷大,损失值非常大。
- 当
y
=
0
y=0
y=0时,代价函数
C
o
s
t
(
h
(
x
)
,
y
)
=
−
l
o
g
e
(
1
−
h
(
x
)
)
Cost(h(x),y)=-log_e(1-h(x))
Cost(h(x),y)=−loge(1−h(x))
当 y = 0 y=0 y=0时, h ( x ) h(x) h(x)为1, C o s t ( h ( x ) , y ) = − l o g e ( 1 − h ( x ) ) Cost(h(x),y)=-log_e(1-h(x)) Cost(h(x),y)=−loge(1−h(x))预测值为1的概率为0, l o g ( 1 − h ( x ) ) log(1-h(x)) log(1−h(x))为无穷大;反之 h ( x ) h(x) h(x)为0,趋向于 y = 0 y=0 y=0的类别, − l o g e 1 = 0 -log_e1=0 −loge1=0,损失最小。
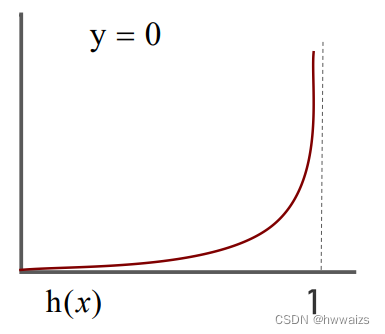
注意:对于逻辑回归来说,不需要区分预测概率类别。当 h ( x ) = P > = 0.5 h(x)=P>=0.5 h(x)=P>=0.5,划分为1这个类别,趋近于1;当 h ( x ) = P < 0.5 h(x)=P<0.5 h(x)=P<0.5,划分到0这个类别,趋近于0。
以上两个代价函数是个分段的,求解 θ θ θ值时要解决实际的问题,而 y = 0 或 1 y=0或1 y=0或1,可以简化方程式来求代价函数,把以上两个式子整合成一个,方便后期的求导。 C o s t ( h ( x ) , y ) = − y l o g e ( h ( x ) ) − ( 1 − y ) l o g e ( 1 − h ( x ) ) Cost(h(x),y)=-ylog_e(h(x))-(1-y)log_e(1-h(x)) Cost(h(x),y)=−yloge(h(x))−(1−y)loge(1−h(x))
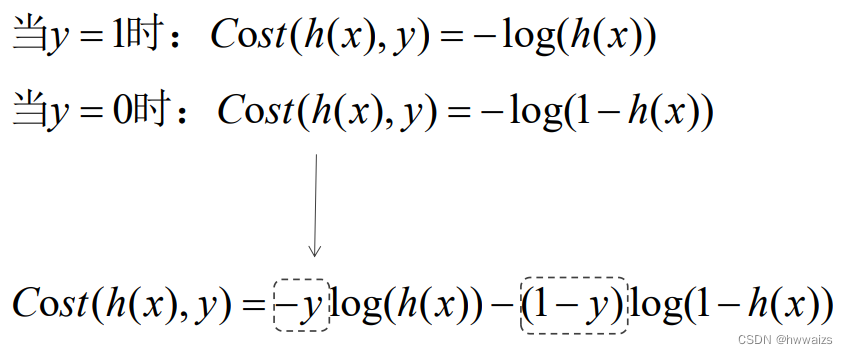
C o s t ( h ( x ) , y ) Cost(h(x),y) Cost(h(x),y)为一个样本数据的损失,每个样本点都有损失,要将很多个样本点进行整合,进行求和除以样本的个数,将负号提出来,得到以下的式子,这种方式也为交叉熵。
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h ( x ) , y ) = − 1 m ∑ i = 1 m [ y l o g e ( h ( x ) ) + ( 1 − y ) l o g e ( 1 − h ( x ) ) ] J(θ)= \frac{1}{m}\displaystyle{\sum_{i=1}^{m}Cost(h(x),y)}=-\frac{1}{m}\displaystyle{\sum_{i=1}^{m}[ylog_e(h(x))+(1-y)log_e(1-h(x))]} J(θ)=m1i=1∑mCost(h(x),y)=−m1i=1∑m[yloge(h(x))+(1−y)loge(1−h(x))]
逻辑回归是很常用的算法,也用于深度学习中。这个方程式运用了统计学中的极大自然法,为不同的模型快速找出参数,同时也是个凸函数,解决了之前非凸函数的问题,便于接下来的求导。
梯度下降法推导
代价函数:
J
(
θ
)
=
=
−
1
m
∑
i
=
1
m
[
y
l
o
g
e
(
h
(
x
)
)
+
(
1
−
y
)
l
o
g
e
(
1
−
h
(
x
)
)
]
J(θ)= =-\frac{1}{m}\displaystyle{\sum_{i=1}^{m}[ylog_e(h(x))+(1-y)log_e(1-h(x))]}
J(θ)==−m1i=1∑m[yloge(h(x))+(1−y)loge(1−h(x))]
目标:求
θ
θ
θ,使得代价函数
J
(
θ
)
J(θ)
J(θ)最小。
换元法,
z
=
θ
T
X
z=θ^TX
z=θTX,对
g
(
z
)
g(z)
g(z)的求导就变为了对
1
1
+
e
−
z
\frac{1}{1+e^{-z}}
1+e−z1进行求导,
1
+
e
−
z
1+e^{-z}
1+e−z求导,就变为了
e
−
z
e^{-z}
e−z导数乘以
−
z
-z
−z的导数,对
z
=
θ
T
X
z=θ^TX
z=θTX求导,X为常数,
θ
T
θ^T
θT为变量,求导后为
x
x
x
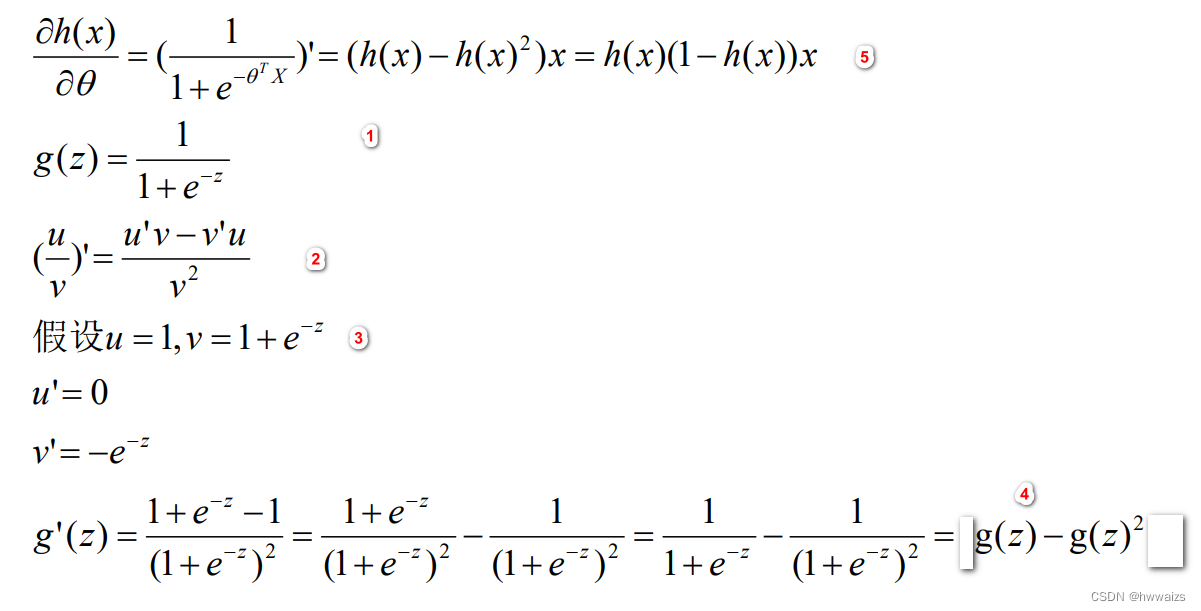
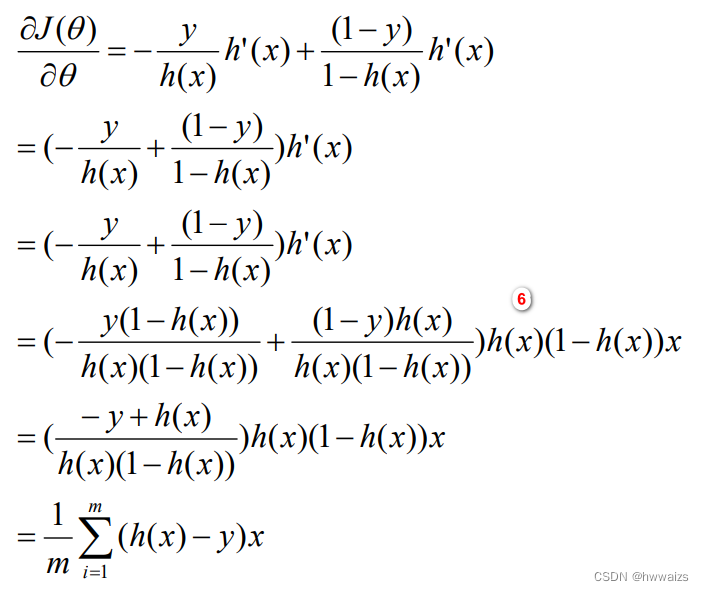
代价函数求导之后的结果为:
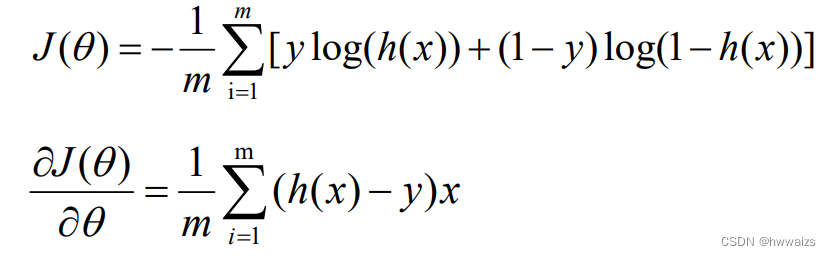
梯度下降法的本质是通过不停的求导,迭代曲线下降的方向,是凸优化的问题,通过求导决定曲线下降的速度和方向,最快的达到最低点,损失最小的过程
l
o
g
e
x
=
l
n
x
=
1
x
log_ex=lnx=\frac{1}{x}
logex=lnx=x1
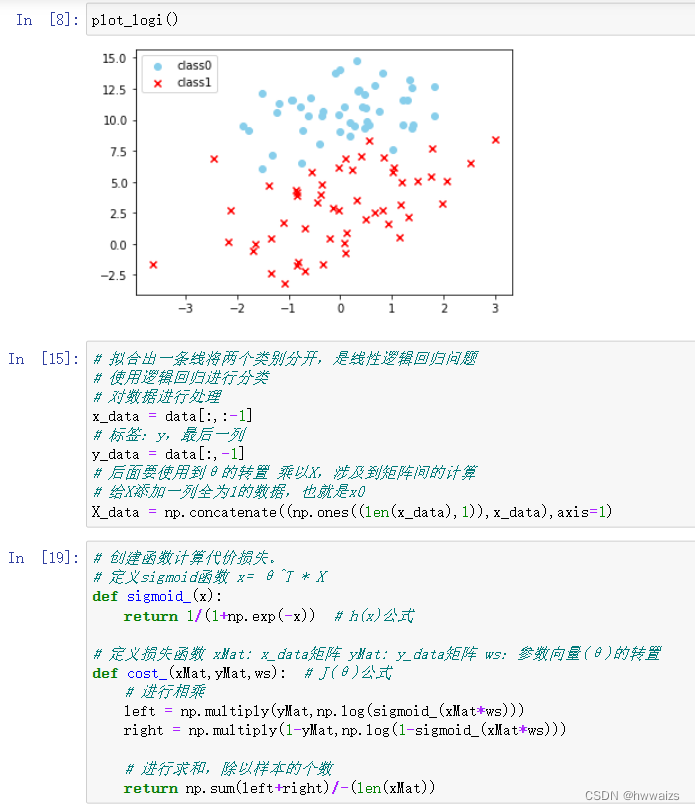
梯度下降法实现线性逻辑回归


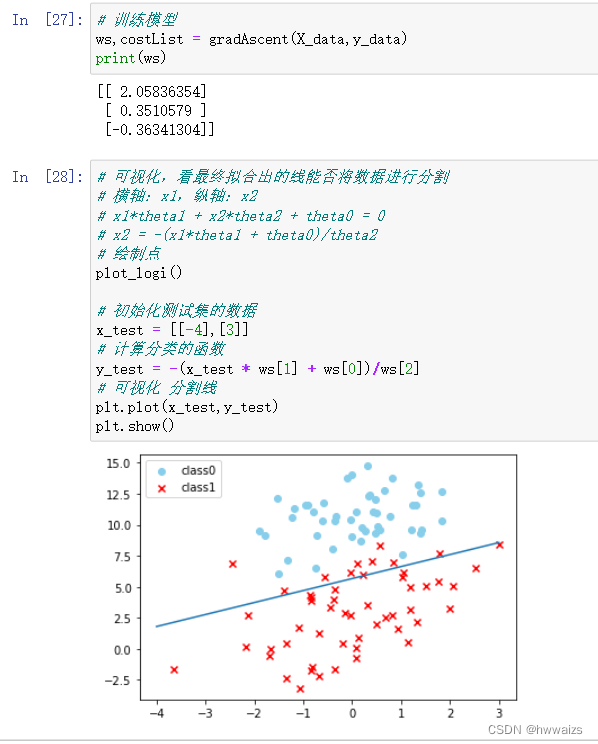
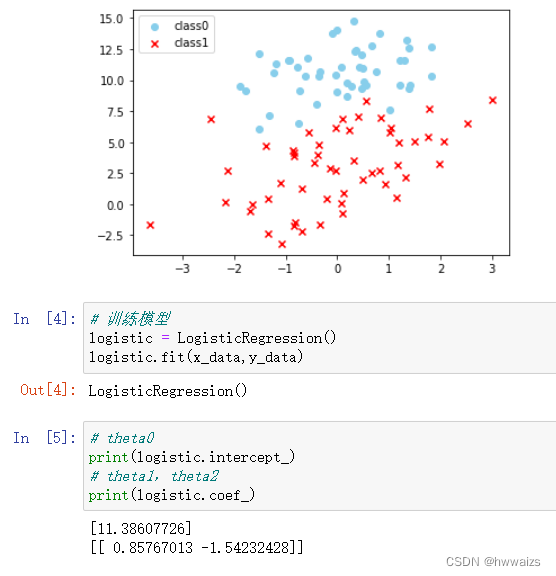
sklearn实现线性逻辑回归
逻辑回归API
sklearn.linear_model.LogisticRegression(solver='liblinear',penalty='l2',C=1.0,
solver 可选参数:{'liblinear','sag','saga','newton-cg','lbfgs'}
penalty:正则化的种类
C:正则化力度
liblinear为默认值,是优化问题的算法,适用于小数据集;sag,saga用于大型数据集,newton-cg用于多类的问题。
数据中有正例和反例,sklearn接口默认将数量少的作为正例。

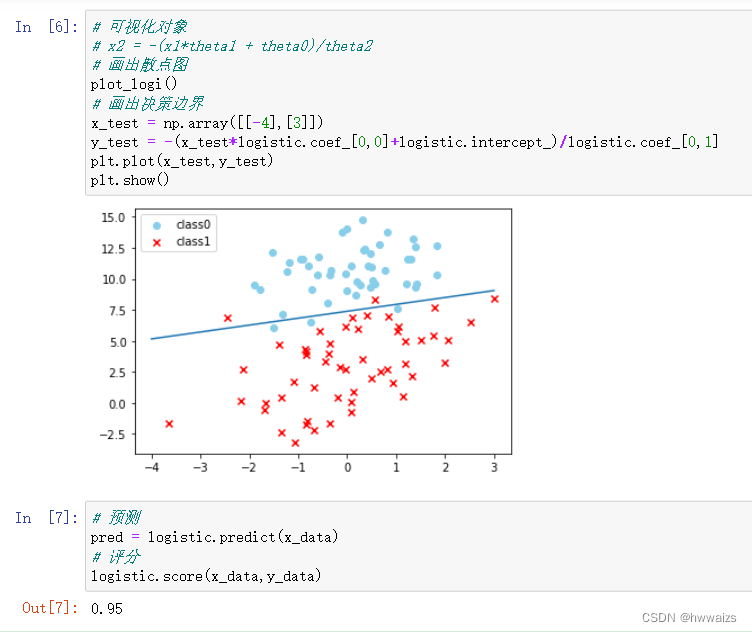
梯度下降法实现非线性逻辑回归
分类评估报告API
sklearn.metrics.classification_report(y_true,y_pred,labels=[],target_names=None)
y_true:真实目标值
y_pred:估计器预测目标值
labels:指定类别对应的数字
target_names:目标类别名称
return:每个类别精确率与召回率
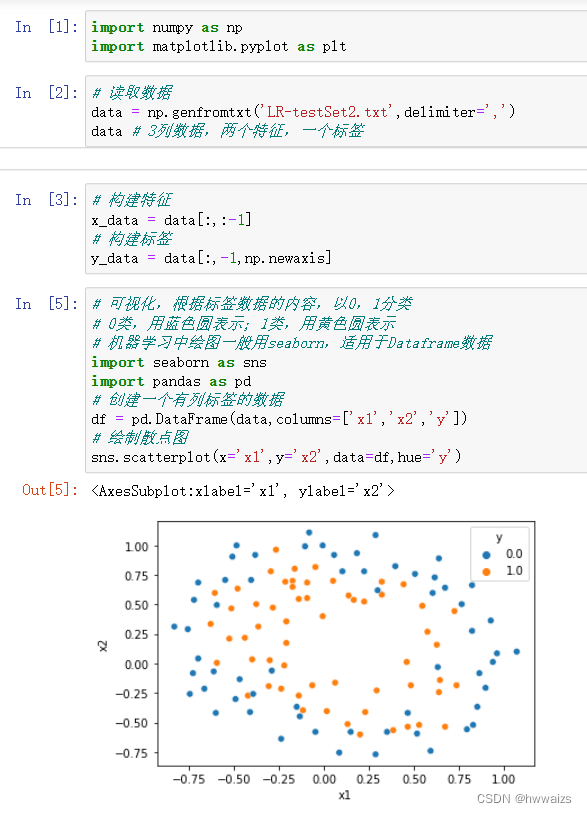



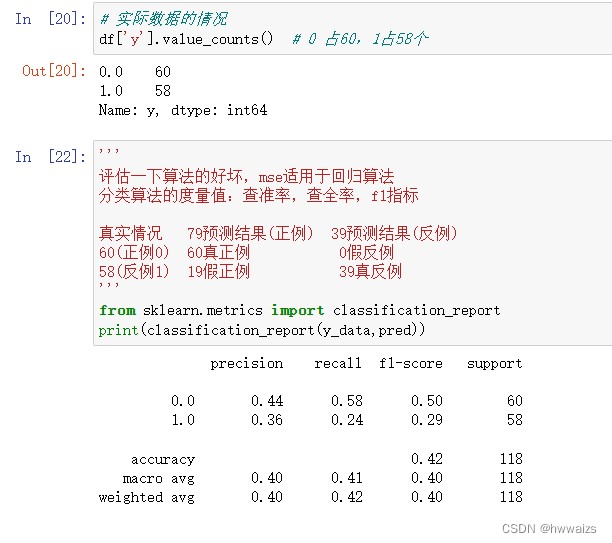
使用sklearn提供的数据集