前置知识

向量的叉乘: 设$\vec{a}=(x_a,y_a,z_a),\vec{b}=(x_b,y_b,z_b)$, 令$\vec{a}$和$\vec{b}$的叉乘为$\vec{c}$, 有:
$$\vec{c}=\left|\begin{array}{ccc}i& j& k\\ x_a& y_a& z_a\\ x_b& y_b& z_b\end{array}\right|=(y_a{z}_b-z_a{y}_b,z_a{x}_b-x_a{z}_b,x_a{y}_b-y_a{x}_b)$$
几何意义: $|\vec{c}|=|\vec{a}\times \vec{b}|=|\vec{a}||\vec{b}|sin\theta$ ($\theta$为$\vec{a}$，$\vec{b}$向量之间的夹角), 即$|\vec{c}|$ 等于$\vec{a}$,$\vec{b}$向量构成的平行四边形的面积.
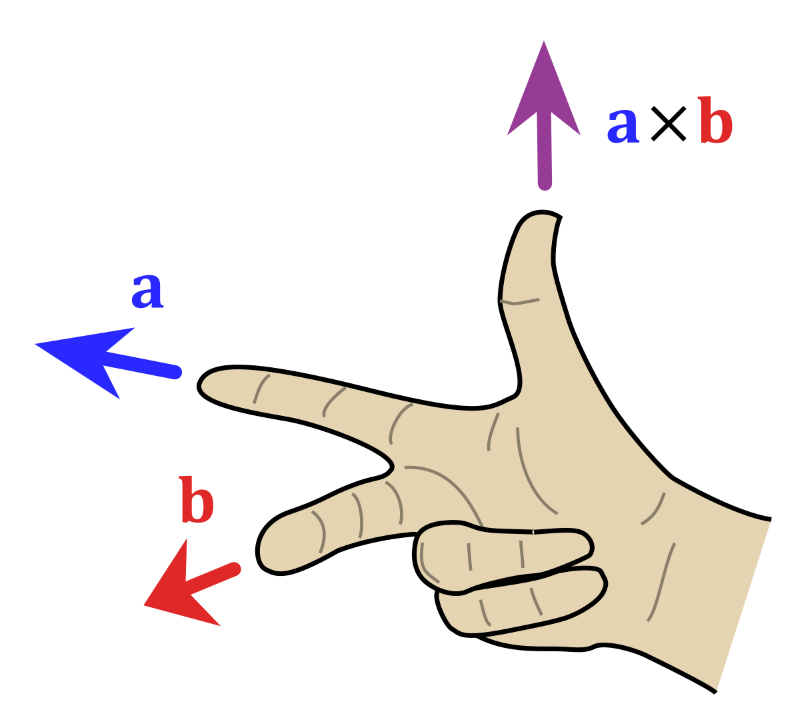
另外$\vec{c}$的方向可以用右手螺旋定则判定: 先将$\vec{a}$和$\vec{b}$移动到同一起点, 右手四指从$\vec{a}$方向朝掌心方向旋转到$\vec{b}$方向, 则拇指所指方向, 即为结果向量的方向.

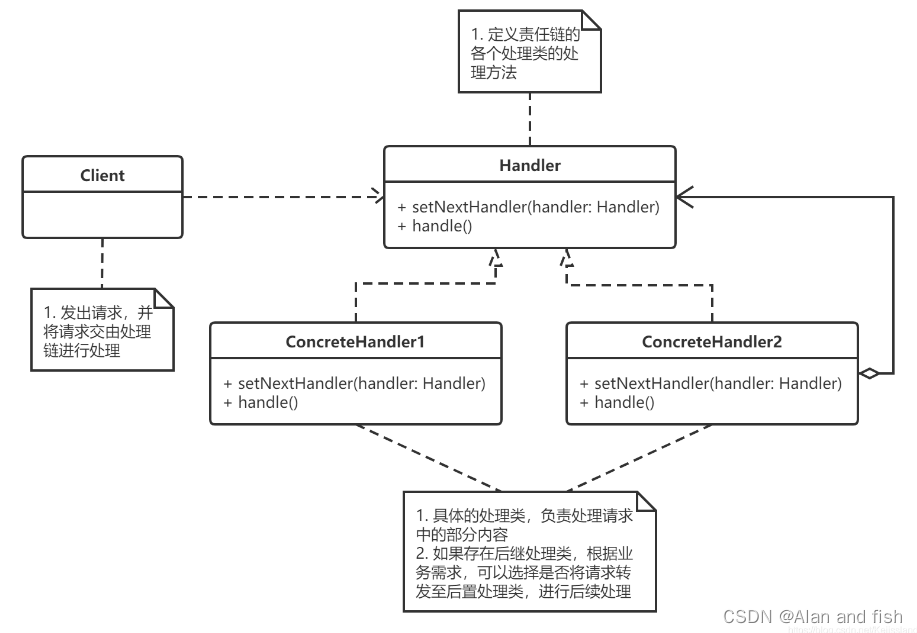
PIP 问题

理解了上述的叉乘的知识, 我们就可以解决PIP这个经典问题的一个子集: 判断一个点是否在一个凸多边形内部. 判断算法的一个伪代码如下:

设$p_0,\cdots ,p_{n-1}$为凸多边形边界上的点按逆时针方向遍历形成的一个排列, $x$为待判断的点
for $i$ in { 0 , ⋯   , n − 1 } \{0,\cdots,n-1\} {0,⋯,n−1}
         \;\;\;\; 若$(\overrightarrow{p_i{p}_{(i+1)\%n}}\times \overrightarrow{p_{(i+1)\%n}x})\cdot (0,0,1)<0$, 则$x$不在多边形内部
$x$在多边形内部(包括边界上)

求凸包

上面提到的伪代码需要凸多边形边界上的点的一个逆时针的排列, 但如过这个排列没有给出, 这时候就可以用Andrew凸包算法来求这样的一个排列, Andrew算法大致思想如下:

首先把所有点以横坐标为第一关键字，纵坐标为第二关键字排序。显然排序后最小的元素和最大的元素一定在凸包上。而且因为是凸多边形，我们如果从一个点出发逆时针走，轨迹总是「左拐」的，一旦出现右拐，就说明这一段不在凸包上。因此我们可以用一个单调栈来维护上下凸壳。

下面贴一个Andrew算法的模板

inline pair<int, int> vec_ab(pair<int, int> a, pair<int, int> b) {
    return {b.first - a.first, b.second - a.second};
}

inline int cross_prod(pair<int, int> a, pair<int, int> b) {
    return a.first * b.second - a.second * b.first;
}

const int maxn = 2e5 + 5;
pair<int, int> p[maxn], h[maxn];
int stk[maxn];
int used[maxn];


int main() {
// stk[] 是整型，存的是下标
    int n;
    int tp=0 // 初始化栈
    //读入p
    std::sort(p + 1, p + n + 1);  // 对点进行排序
    stk[++tp] = 1;
// 栈内添加第一个元素，且不更新 used，使得 1 在最后封闭凸包时也对单调栈更新
    for (int i = 2; i <= n; ++i) {
        while (tp >= 2 && cross_prod(vec_ab(p[stk[tp - 1]], p[stk[tp]]), vec_ab(p[stk[tp]], p[i])) < 0)//凸包边上的点不算在结果数组内(否则用<0)
            used[stk[tp--]] = 0;
        used[i] = 1;  // used 表示在凸壳上
        stk[++tp] = i;
    }
    int tmp = tp;  // tmp 表示下凸壳大小
    for (int i = n - 1; i > 0; --i)
        if (!used[i]) {
            // ↓求上凸壳时不影响下凸壳
            while (tp > tmp && cross_prod(vec_ab(p[stk[tp - 1]], p[stk[tp]]), vec_ab(p[stk[tp]], p[i])) < 0)//凸包边上的点不算在结果数组内(否则用<0)
                used[stk[tp--]] = 0;
            used[i] = 1;
            stk[++tp] = i;
        }
    for (int i = 1; i < tp; ++i)  // 复制到新数组中去
        h[i] = p[stk[i]];
    int ans = tp - 1; // ans为凸包边上节点数

参考:
https://oi-wiki.org/geometry/convex-hull/
https://zhuanlan.zhihu.com/p/385131501