算法简介：

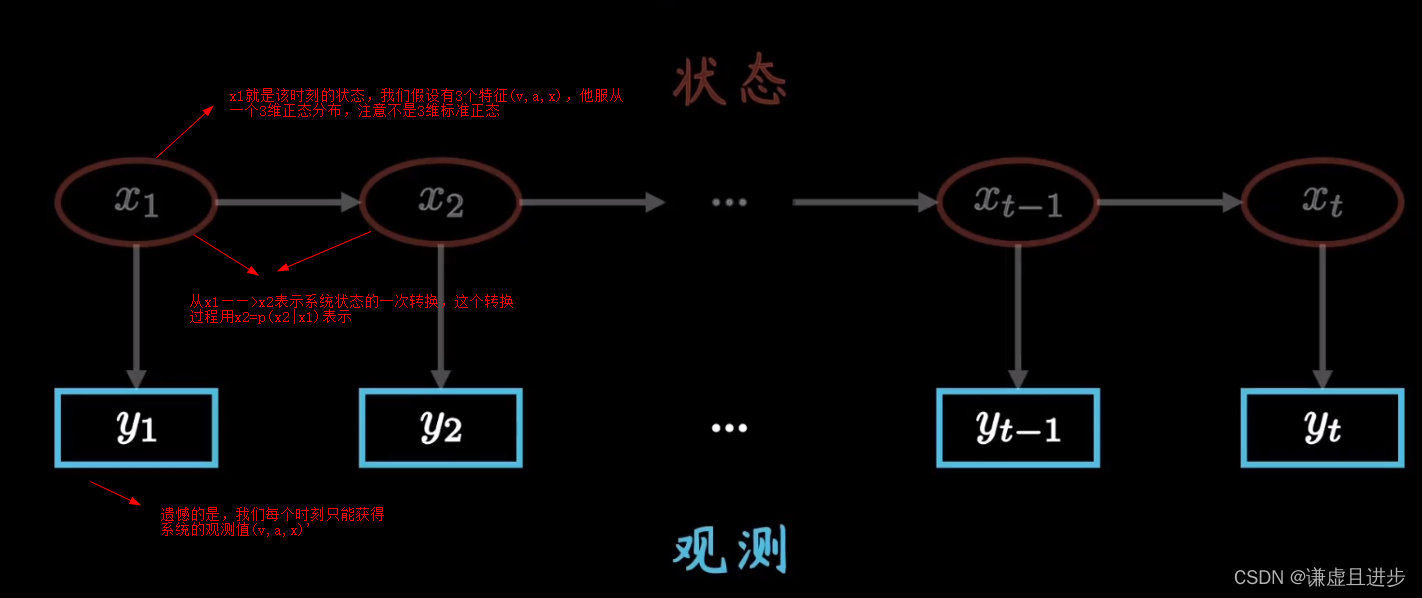
        一个系统每时每刻都存在着不同的状态，他们的状态由各种复杂的机制形成，且状态随着变化而不断改变，而这些复杂的机制就是一些高度非线性且复杂的射关系。

        举一个例子。例如：一辆汽车在一条从左往右的道路上行驶，我们用3个特征来描述这辆汽车的状态，分别是速度、加速度、和位移。在T时刻，我们记这三个特征为一个向量Vt=(v,a,x)，很明显这只是我们观测得到的值，不能代表汽车运动时的真正状态。此外，我们可以认为任意时刻这辆车的运动状态都服从一个3维度的正态分布，但是这个正态分布的表达式很难求，我们只能去近似得到，方法有很多，例如贝叶斯公式、神经网络、GAN等。

        隐马尔可夫过程就是要弄明白一个系统状态转换时是如何进行转换的，目的时求出这个转换过程中的数学表达式。它假设t时刻的状态只与上一个t-1时刻的状态有关系，t时刻的状态取值是t-1时刻的值通过条件概率计算得到。但是问题就是，我们只能得到每一个时刻的观测值，即并不是系统状态的真实值。隐马尔可夫的隐字是因为这个过程中系统状态是未知的。

 

一，HMM应用之滤波flitering

        滤波就是预测，已知历史时刻T-n至T的观测状态值，估计T时刻的系统状态。

二，HMM应用之平滑smoothing

        平滑就是已知历史时刻T-n至T的观测状态值，估计中间时刻T-n-k的系统状态。

三，HMM应用之解码Decoding

        解码一句话概括就是：已知历史时刻T-n至T的观测状态值，去近似求系统转换过程的条件概率分布表达式。

四，马尔科夫链的拓展

        一般马尔可夫只在一个方向进行演变，如果存在向多个方向进行演变的情况就称为马尔可夫随机场，即从线到面的升维。

        由于马尔可夫过程的转换概率表达式很复杂，参数长通过蒙特卡洛方法获取，由此衍生出MCMC方法，即马尔可夫蒙特卡罗方法。

参考：b站耿直哥