第一题：移除元素

请添加图片描述

思路一：

一：暴力查找的方法：
1.找到对应val值的下标，返回数组的下标。
2.删除对应的下标，从前向后用后面覆盖前面。当后一个是数组最后一个数值是就赋值结束了（注意数组越界的问题）。
3.删除了一个数之后数组元素个数要–。
4.查找和删除是在一个循环里面因为val的值可能在数组中出现多次，直到返回的下标的值没有了，就结束了循环，val的数值都移除完了。

// 顺序表查找
int SeqListFind(int* ps, int x,int nume)
{
	//遍历查找
	int n = nume;
	for (int i = 0; i < n; i++)
	{
		if (ps[i] == x)
		{
			return i;
		}
	}
	return -1;
}
// 顺序表删除pos位置的值
void SeqListErase(int* ps, int pos,int num)
{
	int n = num;
	for (int i = pos; i < n-1; i++)
	{
		ps[i] = ps[i+1];
	}
}


int removeElement(int* nums, int numsSize, int val){
    while(1)
    {
        int b=SeqListFind(nums,val,numsSize);
        if(b==-1)
        {
            break;
        }
        else
        {
            SeqListErase(nums,b,numsSize);
            numsSize--;
        }
    }
    return numsSize;
}

思路二：

二：使用双指针的方法
1.不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。
2.定义两个下标：src和dis，他们开始的时候是在一起的对应的数组值都不是val的时候，同时++。
3.只要src位置是val就src++；
4.当src位置不是val就把src位置的值赋值到dis，到src>n-1循环结束

int removeElement(int* nums, int numsSize, int val)
{
    int src=0;
    int dis=0;
    int n=numsSize;
    int count=0;
    while(src<=n-1)
    {
        if((src==dis) && (nums[src]!=val))
        {
            src++;
            dis++;
        }
        else if((nums[src]==val))
        {
            src++;
            count++;
        }
        else if((nums[src]!=val))
        {
            nums[dis]=nums[src];
            src++;
            dis++;
        }
    }
    return n-count;
}

第二题：

请添加图片描述
第二题：

思路一：

一.双指针的方法
1.定义p1,p2 两个变量，初始化为0从两个数组开头开始向后移动。
2.同时比较nums1[p1]和nums2[p2]这两个位置的数值。
3.开辟一个新的数组大小为m+n两个数组长度的和。
4.在比较的过程中较小的值放到新的数组，开辟数组的下标++，小的值的数组的下标++。
5.结束条件p1>=m 中有一个 p2>=n就结束。
6.出来之后另一个没有放完，p1=m,说明nums2没有放完。反之同理。
7.tmp拷贝回去到nums1中
空间复杂度是O（N）时间复杂度O（2*（M+N））；

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    int p1=0;
    int p2=0;
    int* tmp=(int*)malloc(sizeof(int)*(m+n));
    int i=0;

    while((p1<m)&&(p2<n))
    {
        
        if(nums1[p1]>=nums2[p2])
        {
                *(tmp+i)=nums2[p2];
                p2++;
                i++;
                continue;
        }

        else if(nums1[p1]<nums2[p2])
        {
                *(tmp+i)=nums1[p1];
                p1++;
                i++;
                continue;
        }
    }

     if(p1>m-1)
        {
            memcpy(tmp+i,nums2+p2,sizeof(int)*(n-p2));
        }
     else if(p2>n-1)
        {
            memcpy(tmp+i,nums1+p1,sizeof(int)*(m-p1));
        }



    memcpy(nums1,tmp,sizeof(int)*(m+n));
}

思路二：

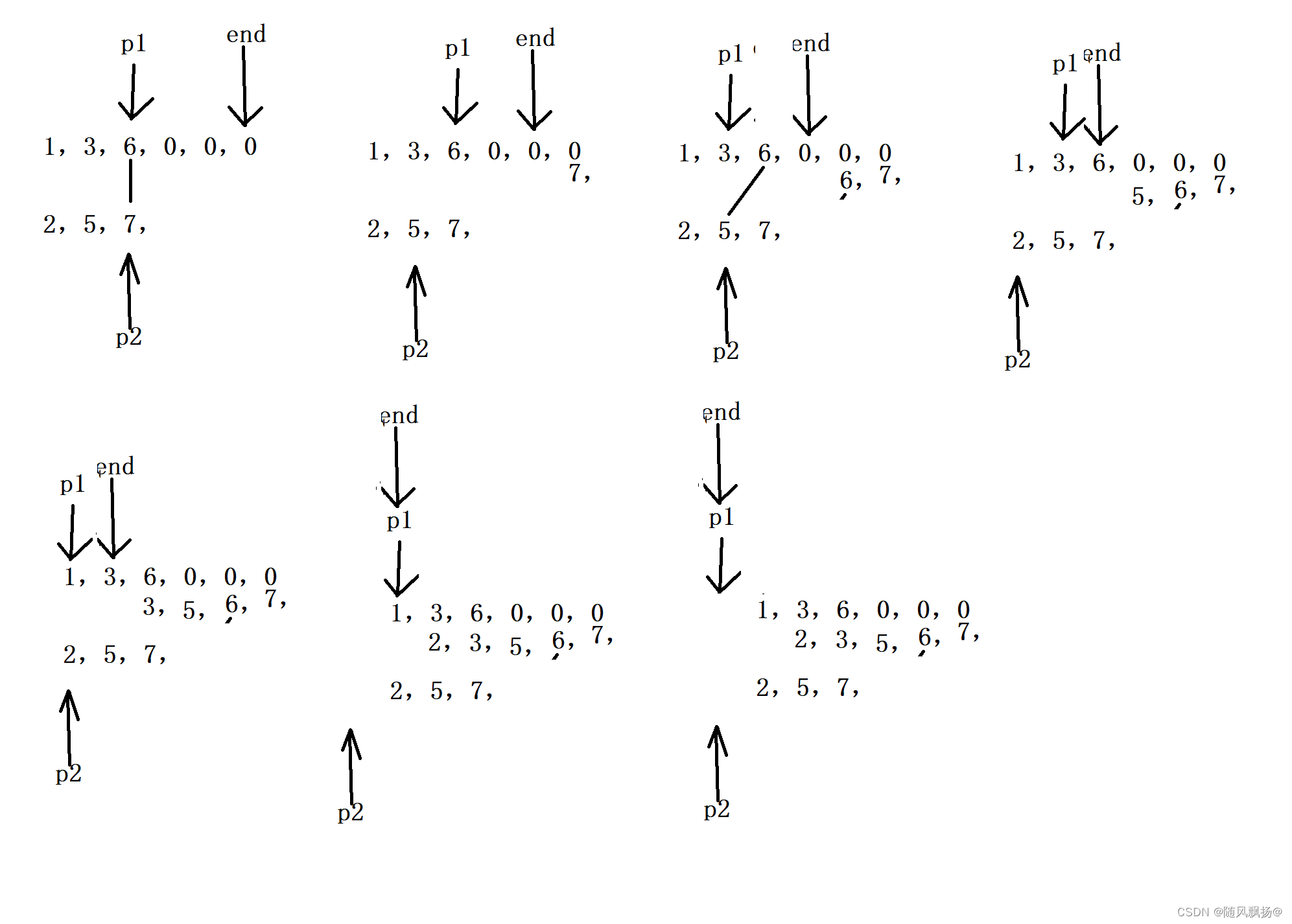
三指针的方法：
1.p1起始位置是m-1，p2起始位置是n-1.数组值的尾。
2.end起始位置是（m+n）-1在nums1上。
3.分别从尾开始比较赋值到nums1[end]位置，谁赋值过去对应的p就–，end–。
4.当p1==-1,p2还没有结束需要把值赋值到对应的num1上。
5.当p2==-1就说明已经结束。
时间复杂度优化到了O（m+n）

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){

        int p1=m-1;
        int p2=n-1;
        int end=(m+n)-1;

        while(p1>=0 && p2>=0)
        {
            if(nums1[p1]>nums2[p2])
            {
                nums1[end]=nums1[p1];
                p1--;
                end--;
            }
            else
            {
                nums1[end]=nums2[p2];
                p2--;
                end--;
            }
        }

        while(p2>=0)
        {
            nums1[end]=nums2[p2];
            p2--;
            end--;
        }
}