46. 全排列
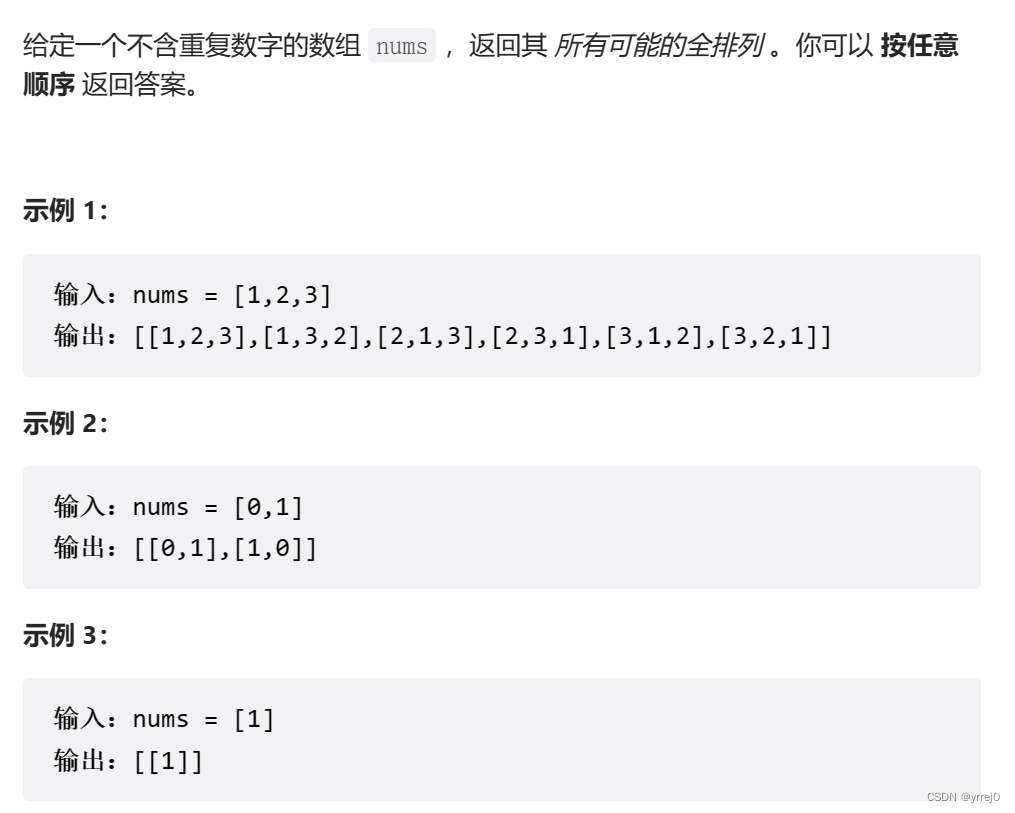
思路:这道题首先是一个排列问题,排列问题是讲究顺序的,例如[1,2]和[2,1]是两个不一样的排列,这里的1我们会有重复使用到,但是,在每一个排列中,每一个元素只能使用一次。所以需要一个状态数组初始化为false *len(nums)来标记。当我们第一次使用的时候发现这个元素没有被用过就加入到path中,加入完了之后要把他的状态变为true,标识我们当前这个元素已经用过了。然后进行撤销,因为我们已经把这个排列加入了结果集中,收获到了结果,需要进行回溯 回到上一层,然后再次从头开始搜索,这里状态就又要成为false.
回溯三部曲:
递归参数:因为是排列问题,每个组合都会重复用到一个元素,就不需要startindex了,这里只需要一个index,我们最后调用的时候从0开始调用就行。所以参数是nums,index.
终止条件: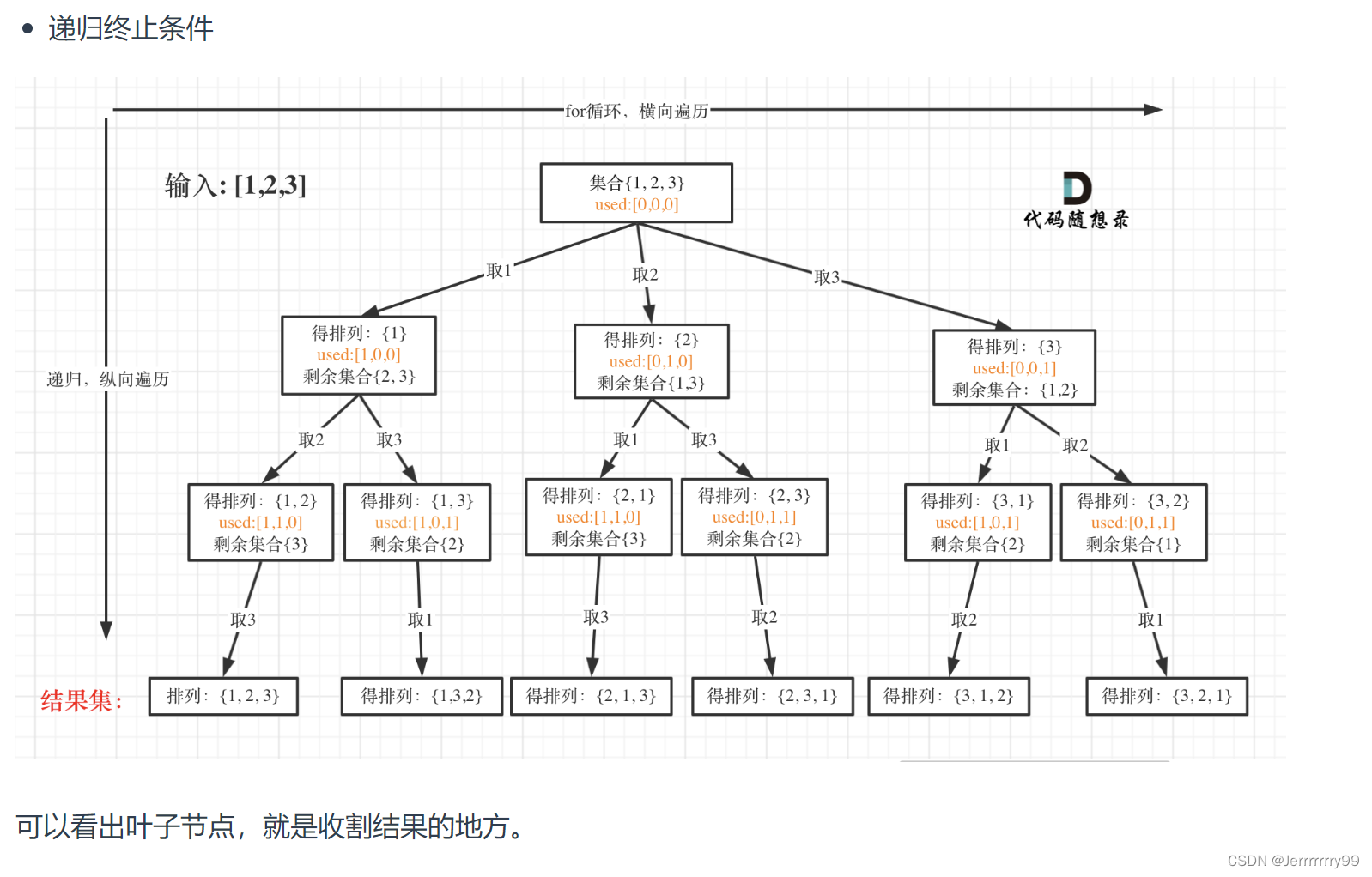
当我们的收获到的path的长度已经和nums的长度一样了,说明我们完全遍历完了,也就是该收获的时候了,所以加入结果集然后return
单层循环逻辑:if used[i]==false,那我们就加入到path中,开始递归 改变状态 然后回溯+撤销。
代码:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
track = []
used = [False] * len(nums)
def back_trace(nums,index):
if len(track)==len(nums):
#深度优先遍历时,返回列表是为空的
res.append(track[:])
return
for i in range(len(nums)):
'如果当前节点没有被访问过'
if used[i]==False:
'就加入到track中并且状态改为已访问'
track.append(nums[i])
used[i]=True
'回溯'
back_trace(nums,0)
track.pop()
used[i] = False
else:
continue
back_trace(nums,0)
return res47. 全排列 II
和上一个题不一样的是,nums数组中出现了重复的元素,并且我们的输出结果中,也有重复的元素,但是要求返回不重复的排列
这就是涉及到了我们的去重操作,在前面都有提到过,关于组合和子集的去重方式。
转换为树的结构来看
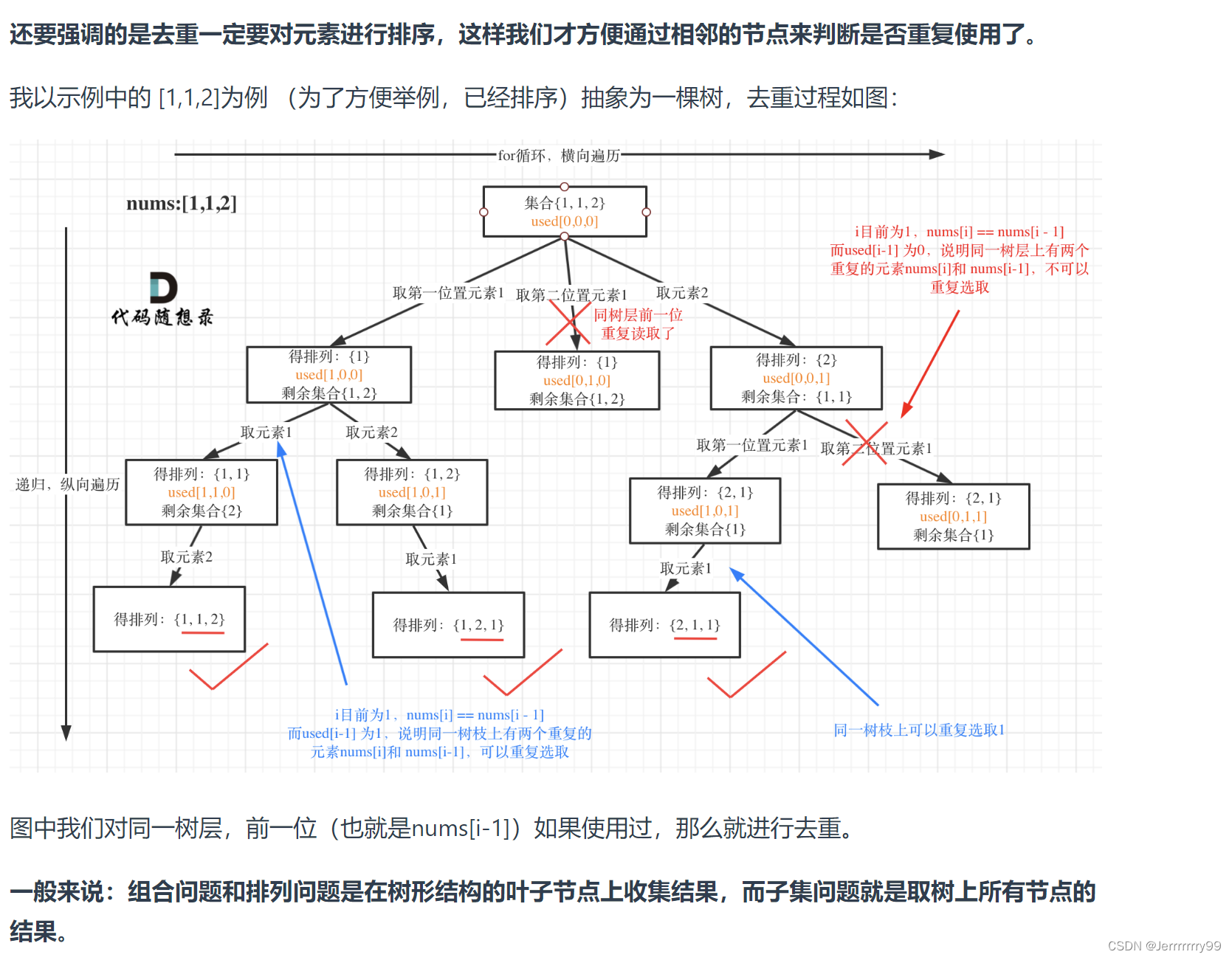
分为了树枝去重和树层去重,这个题是数层去重,也就是同一层,前面用过的元素后面不能再用了。
但是树枝是可以重复使用的。
首先要做的就是对nums数组进行排序,通过相邻的数字判断是否有被用过。
回溯三部曲:
递归参数:nums,index
终止条件:同样的,如果path的长度等于数组的长度,说明找到了一组
单层循环逻辑:if i>0&当前元素等于前一个元素&并且前一个元素没有被使用过
那么就continue循环。否则加入path 然后递归回溯撤销一起走
为什么这里我们要判断上一个元素没有被使用过呢?
实际上是因为我们第一次在做撤销选择的时候,将他的状态码改为了false。实际上在这一层他是已经使用过的。
代码:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
#路径长度
n = len(nums)
nums.sort()
#答案数组
res = []
#路径数组
path = []
#当前状态
stats = [False] * n
def dfs(index,nums):
if len(path)==n:
res.append(path[:])
return
for i in range(n):
if stats[i]==False:
'''如果上一个数字和当前数字相同并且上一个数字没有被使用过,那就继续循环'''
if i >0 and nums[i-1]==nums[i] and stats[i-1]==False:
continue
path.append(nums[i])
stats[i]=True
#回溯
dfs(0,nums)
stats[i]=False
path.pop()
dfs(0,nums)
return resleetcode491递增子序列
力扣

思路:
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
这又是子集,又是去重,是不是不由自主的想起了刚刚讲过的90.子集II (opens new window)。
就是因为太像了,更要注意差别所在,要不就掉坑里了!
在90.子集II (opens new window)中我们是通过排序,再加一个标记数组来达到去重的目的。
而本题求自增子序列,是不能对原数组经行排序的,排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑!
本题给出的示例,还是一个有序数组 [4, 6, 7, 7],这更容易误导大家按照排序的思路去做了。
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
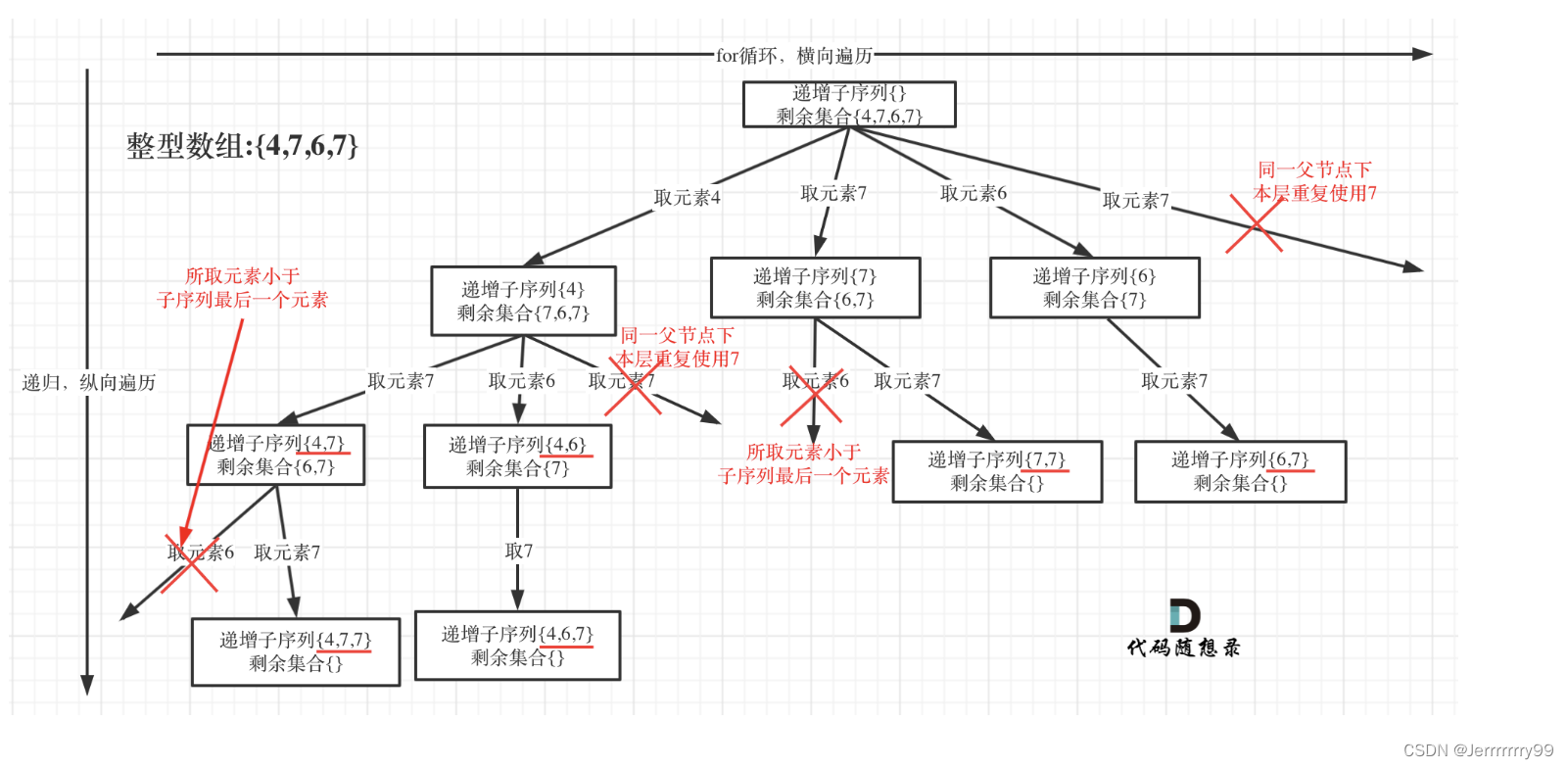
首先明确两点:在树的同一层下,重复的元素不可以使用
在树的分支上,要和上一个元素进行对比,因为是递增子序列,所以一定要大于等于上一次的元素。
回溯三部曲:终止条件,当我们的startindex已经等于数组长度的时候,说明遍历完毕,可以return了
递归参数:nums,startindex,然后需要初始化我们的path和result结果集
单层逻辑:这里我们创建一个set(),深度遍历的时候,每一层都会创建一个新的set判断本层元素是否重复使用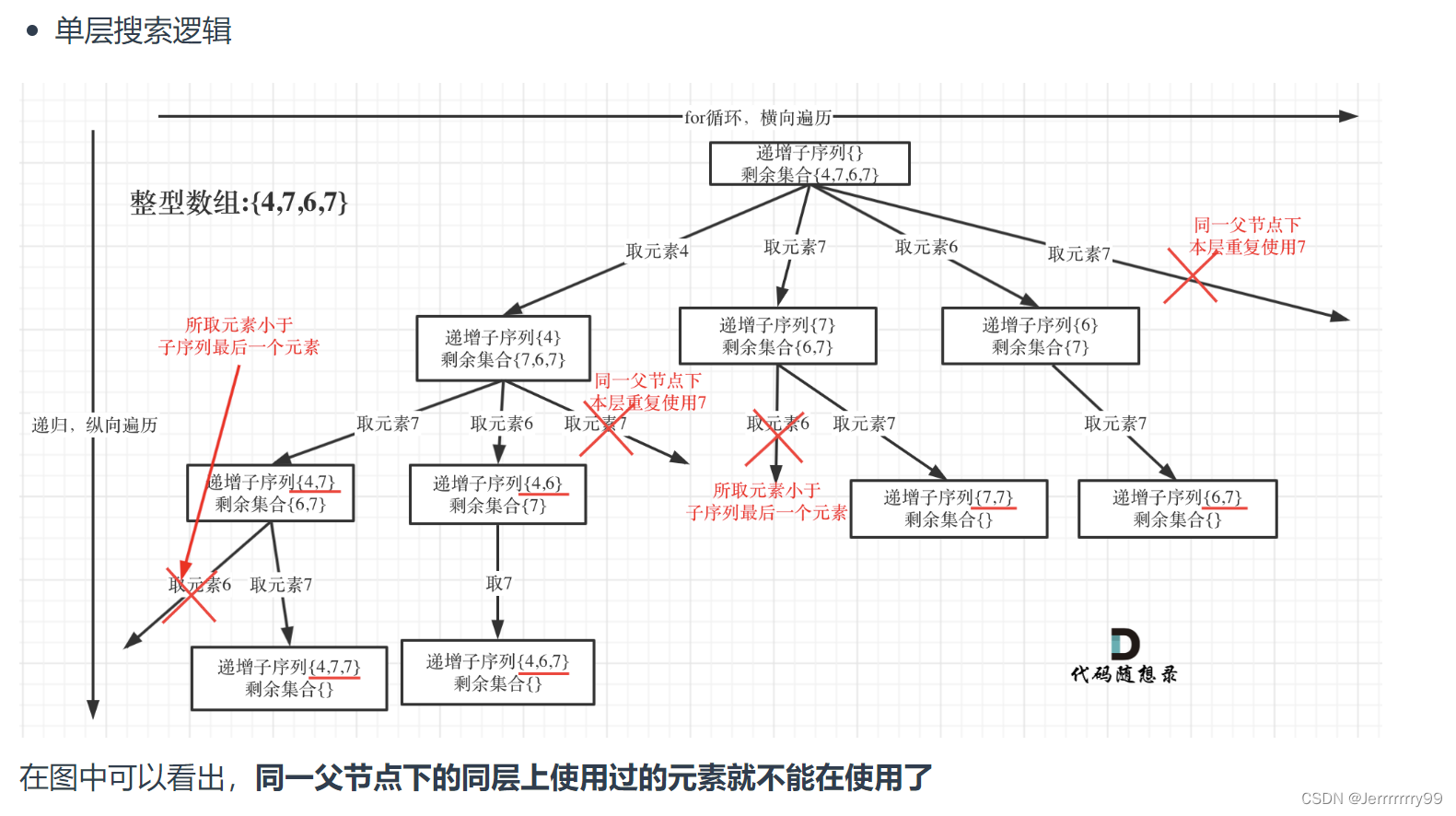
对path路径进行判断是否为空,如果不为空,那就同时判断上一次的元素也就是path[-1]是否大于我们当前的元素,如果上一个元素大于当前元素,或者当前元素已经在我们的used_set中了,那么久continue。否则,我们就加入used_set&path中,然后递归,然后是我们的撤销 回溯
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
self.path = []
self.result = []
self.traceback(nums,0)
return self.result
def traceback(self,nums,startindex):
if len(self.path) >=2:
self.result.append(self.path[:])
#终止条件
if startindex==len(nums):
return
#递归
#同层横向遍历
# 深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用
used_set = set()
for i in range(startindex,len(nums)):
if (self.path and nums[i] < self.path[-1]) or nums[i] in used_set:
continue
used_set.add(nums[i])
self.path.append(nums[i])
self.traceback(nums,i+1)
self.path.pop()

![[Spring] 三级缓存解决循环依赖详解](https://img-blog.csdnimg.cn/76c58cfe480a4920a32de74f8b7b6ff5.png)