含义

递归函数是指能够直接或间接调用自身的方法或函数。

// 直接
function do() {
    do();
}

// 间接
function do() {
    do2();
}
function do2() {
    do()
}

每个递归函数必须有基线条件（即停止点，一个不再递归调用的条件。）否则将无限递归下去。因此有一句编程的名言是：“要理解递归，首先要理解递归”。

function understandRecursion(doIunderstandRecursion) {
  const recursionAnswer = confirm('Do you understand recursion?'); // function logic
  if (recursionAnswer === true) { // base case or stop point
    return true;
  }
  understandRecursion(recursionAnswer); // recursive call
}

例子

迭代阶乘便是迭代函数应用的一个很好的例子。

n!=n * (n-1) * (n-2) ... * 1

function factorial(n) {
    // 基线条件
    if (n  <= 1) {
        return 1
    }
   return n * factorial(n-1)
}

栈的顺序

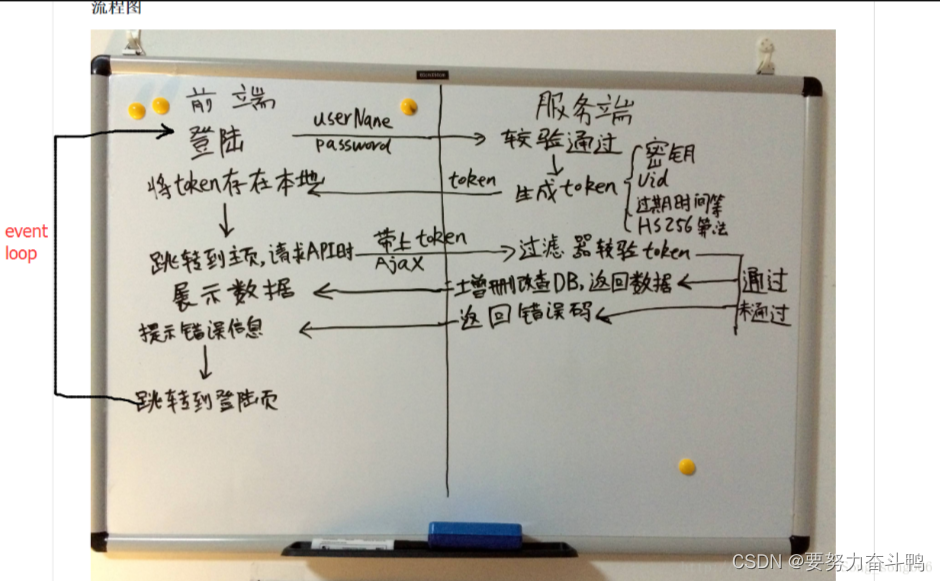
理解递归，需要理解递归时函数执行的调用栈顺序。

当我们执行factorial(3)的时候：

执行步骤为：factorial(3) => 3 * factorial(2) => 2 * factorial(1)

此时函数的执行栈完毕，开始弹出调用栈

factorial(1) => factorial(2) => factorial(3)

我们可以通过浏览器的开发者工具进行观察：

可以看到我们断点的位置在于n为1的时候。此时调用栈里有三个factorial函数。

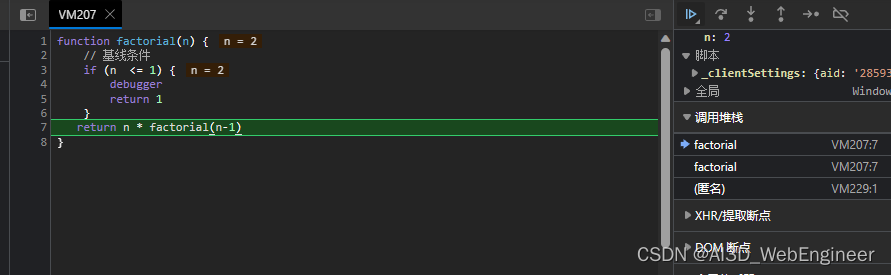
继续往下走，此时n=2。此时剩下两个factorial函数。n=1的factionrial函数已经回调完毕（返回1）。

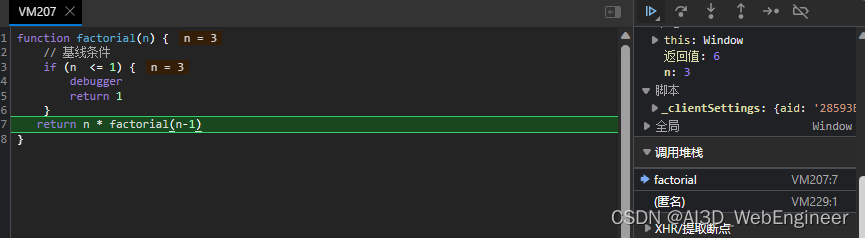
回调factionrial(1)

Js调用栈大小限制

如果忘记加上基线条件，递归函数并不会无限地执行下去。当调用栈堆叠到一定限度。浏览器就会抛出错误。也就是所谓的栈溢出错误。

这个限度是由浏览器自身进行限制的。我们可以通过函数进行测试。

let i = 0;
function recursiveFn() {
  i++;
  recursiveFn();
}

try {
  recursiveFn();
} catch (ex) {
  console.log('i = ' + i + ' error: ' + ex);
}

Edge超限次数为13903 次

这个数值根据操作系统和浏览器不同，会有差异。

ES6有尾调用优化。也就是说如果函数内的最后一个操作是调用函数。会通过“跳转指令”而不是“子程序调用”来控制。也就是说，在ES6中，递归函数可能不受栈溢出限制。因此，具有停止递归的基线条件很重要。

解决斐波那契数列

斐波那契数列是一个由0、1、1、2、3、5、8、13、21、34等数组成的序列。

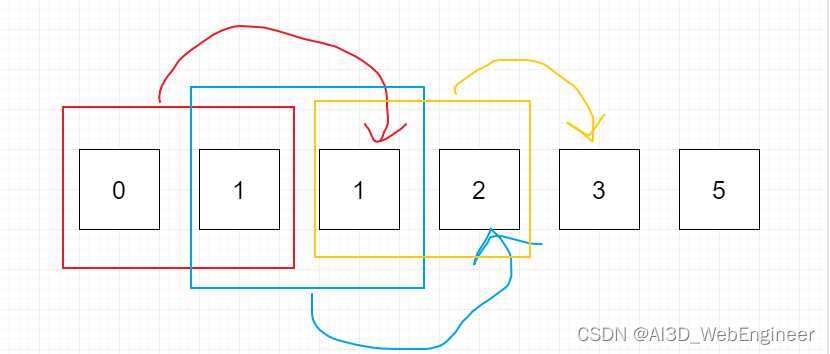
上图是直观上的规律。而抽象出计算机数学规律为：

数列(组)的下标0对应0
数列下标1对应1
数列下标n（n>1）对应下标(n-1)值和下标(n-2)值的和。即value(n) = value(n-1) + value(n-2)

通过数学规律我们可以发现，只要我们特别处理value(0)和value(1)的返回值。其他的都可以交给迭代函数去累加处理。

为了减少迭代次数，我们再优化一下规律：

数列(组)的下标0对应0
数列下标1对应1
数列下标2对应1
数列下标n（n>2）对应下标(n-1)值和下标(n-2)值的和。即value(n) = value(n-1) + value(n-2)

function fibonacci(n) {
    if (n===0) {return 0}
    if (n<=2)  {return 1}
    return fibonacci(n-1) + fibonacci(n-2)
}

调用顺序如图。从左树到右树依次遍历过去。

fibonacci(5) -> fibonacci(4) -> fibonacci(3) -> fibonacci(2) -> fibonacci(1) ->弹出调用栈到fibonacci(3) -> fibonacci(2) -> f弹出调用栈到fibonacci(4) -> ibonacci(3) -> fibonacci(2) -> fibonacci(1)

记忆斐波那契数列

记忆化是一种保存前一个结果的值的优化技术。类似于缓存。比如上面的fibonacci(5)里，fibonacci(3)被计算了两次。若将它结果储存下来，便可以少计算一次了。

function fibonacciMemory(n) {
    const memoryResult = [0,1,1];
    const fibonacci = (n) => {
        if (memoryResult[n] != null) return memoryResult[n];
        return memoryResult[n] = fibonacci(n-1) + fibonacci(n-2)
    }
    return fibonacci(n)
}

用迭代去实现

export function fibonacciIterative(n) {
  if (n < 1) { return 0; }
  let fibNMinus2 = 0;
  let fibNMinus1 = 1;
  let fibN = n;
  for (let i = 2; i <= n; i++) {
    fibN = fibNMinus1 + fibNMinus2;
    fibNMinus2 = fibNMinus1;
    fibNMinus1 = fibN;
  }
  return fibN;
}