1、算法效率

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间

2、时间复杂度：

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间

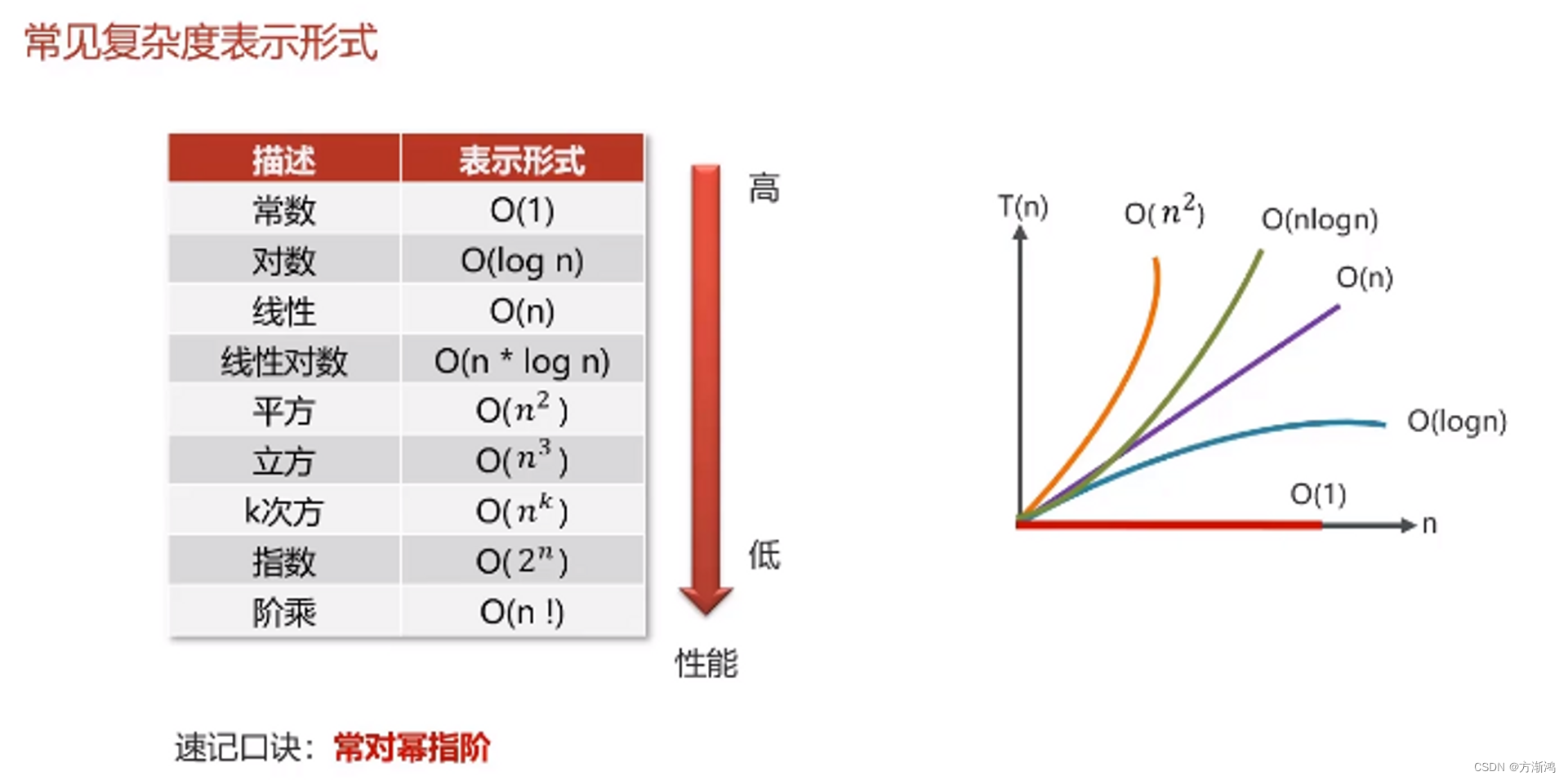
• 大O表示法：不具体表示代码的真正的执行时间，而是表示代码执行时间随着数据规模的增长的变化趋势
• 复杂度分享就是要捋清楚代码的执行次数和数据规模n之间的关系；

1. O(1)：只要代码的执行时间不随着n的增大而增大，这样的代码复杂度都是O(1)。 如：

   public void test01(int n){
   	int i = 0;
   	int sum =  0;
   	for(;1<100;i++){
   		sum = sum + i;
   	}
   }
   

2. O(log n)：变量i的值以对数的方式增长；随着i的值越来越大，i也就离n越近。如：

   public void test01(int n){
       int i=1;
       while (i<n){
           i = i * 2;
       }
   }
   

由以上分析可知，代码的时间复杂度表示为O(log n)

1. O(n)：T(n)与代码的执行次数成正比（代码的执行时间越长，时间复杂度越高）

   public void test01(int n){
   	int i = 0;
   	int sum =  0;
   	for(;i<n;i++){
   		sum = sum + i;
   	}
   }
   

3、空间复杂度：

空间复杂度（Space Complexity）是算法在执行过程中所需的额外空间的量度。它用于评估算法对内存资源的使用情况，包括算法使用的额外内存空间的大小和增长趋势。

1. O(1)：当空间复杂度为 O(1) 时，表示算法使用的额外空间是固定的，与输入规模无关。

    public void printNumbers(int n) {
    for (int i = 1; i <= n; i++) {
        System.out.println(i);
    }
}

2. O(n)：当空间复杂度为 O(n) 时，表示算法使用的额外空间与输入规模成正比。

public int[] copyArray(int[] nums) {
    int[] copy = new int[nums.length];
    for (int i = 0; i < nums.length; i++) {
        copy[i] = nums[i];
    }
    return copy;
}

3. O(n^2) ： 当空间复杂度为 O(n^2) 时，表示算法使用的额外空间与输入规模的平方成正比。

public int[] copyArray(int[] nums) {
    int[] copy = new int[nums.length];
    for (int i = 0; i < nums.length; i++) {
        copy[i] = nums[i];
    }
    return copy;
}