前言
学过c++的多知道,准确的来说是做过c++题目的都知道:c++题目不仅要求代码正确,还要求用时,大多用时要求都在200ms--1000ms之间,要是遇到大数据时,超时的可能就会大大提升。
结论 用时的把控也很重要!
实验
题目
题目描述
小爱想要画一棵 n 个节点的有根树,节点编号分别为1..n,他告诉了你他希望每个节点在这棵树上的深度 di,其中根节点深度为 1。
请你根据给定信息,帮忙计算出有多少棵树满足小爱的要求?由于答案可能很大,请你输出对 10^9+7 取模后的结果。
输入格式
输入共两行,
第一行,一个正整数 n ,表示节点个数
第二行,n 个正整数 d1,d2,...,dn,分别表示每个节点的深度
原代码
#include<bits/stdc++.h>
//#pragma GCC optimize(1,2,3,"Ofast","inline")
#define int long long
using namespace std;
const int N=1e5+10;
const int M=1e9+7;
int n,a,T[N],mx,x=1;
signed main()
{
scanf("%lld",&n);
while(n--)
{
scanf("%lld",&a);
T[a]++;
mx=max(mx,a);
}
for(int i=3;i<=mx;i++)
{
if(T[i-1]>1)
{
for(int j=1;j<=T[i];j++)
{
x=x*T[i-1]%M;
}
}
}
cout<<x;
return 0;
}
用时情况

我们可以发现: 5*10ms 2*20ms
加上快读快写的代码
#include<bits/stdc++.h>
//#pragma GCC optimize(1,2,3,"Ofast","inline")
#define int long long
using namespace std;
const int N=1e5+10;
const int M=1e9+7;
int n,a,T[N],mx,x=1;
signed read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
void write(int x){
if(x<0)
{
putchar('-');
x=-x;
}
if(x>9)
{
write(x/10);
}
putchar(x%10+'0');
}
signed main()
{
n=read();
while(n--)
{
a=read();
T[a]++;
mx=max(mx,a);
}
for(int i=3;i<=mx;i++)
{
if(T[i-1]>1)
{
for(int j=1;j<=T[i];j++)
{
x=x*T[i-1]%M;
}
}
}
write(x);
return 0;
}用时情况

我们可以发现: 3*10ms
加上O1O2O3优化
O1O2O3优化讲解,代码
#include<bits/stdc++.h>
#pragma GCC optimize(1,2,3,"Ofast","inline")
#define int long long
using namespace std;
const int N=1e5+10;
const int M=1e9+7;
int n,a,T[N],mx,x=1;
signed read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
void write(int x){
if(x<0)
{
putchar('-');
x=-x;
}
if(x>9)
{
write(x/10);
}
putchar(x%10+'0');
}
signed main()
{
n=read();
while(n--)
{
a=read();
T[a]++;
mx=max(mx,a);
}
for(int i=3;i<=mx;i++)
{
if(T[i-1]>1)
{
for(int j=1;j<=T[i];j++)
{
x=x*T[i-1]%M;
}
}
}
write(x);
return 0;
}用时情况
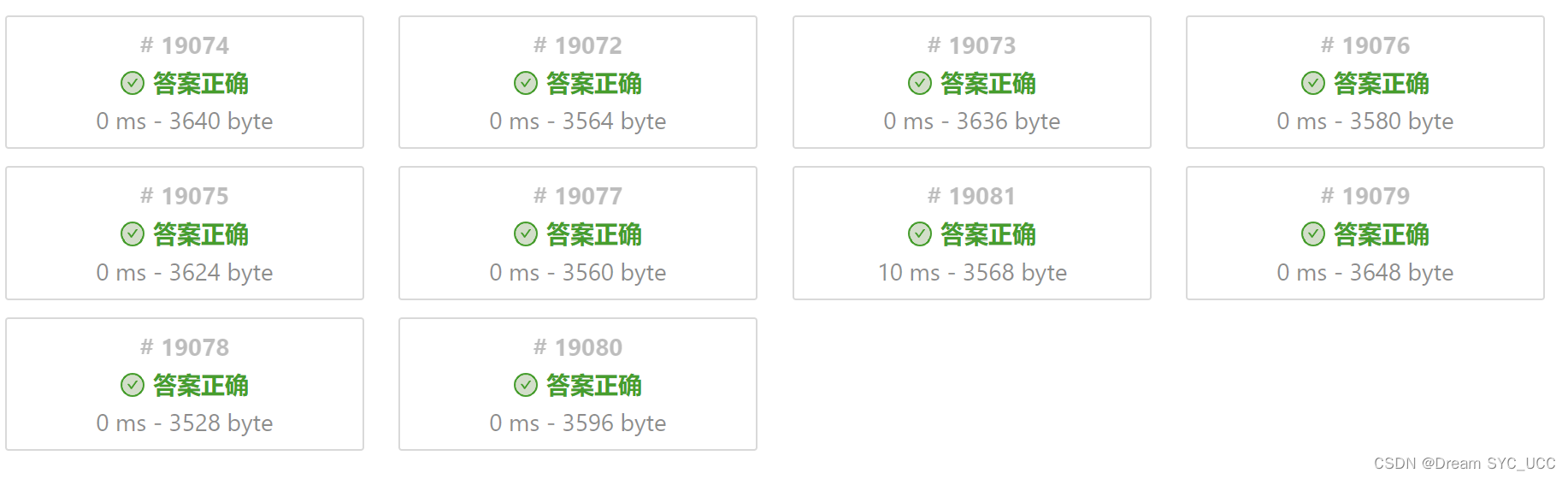
我们发现: 只有一个10ms
总结论
想要快,用快读快些加优化。