逻辑的极限，数学和沉思

发表于康托尔的天堂

当逻辑出错时会发生什么？

让我们看看为什么排除中间定律是错误的（有时），发现数学核心的基本问题，然后再最终尝试解决出了什么问题。

您还将学习如何理解-1的负根，简要深入研究分析，以及仅使用逻辑证明所有克里特人都是骗子。

有了对逻辑、公理和数学的更多理解，我们将发现西方哲学的一些缺陷，特别是在伊曼努尔·康德的先验真理概念（尾声III）中。

在一个美丽的转折中，所提供的数学概念将与德里达提供的“差异”思想相吻合（尾声IV）。在尾声V中，逻辑和决定论之间也有联系。

中间定律:一个陈述要么是真的,要么它的否定是真的。

二价原理:每个陈述要么是真,要么是假。

中间定律说明,对于任意一个陈述P,要么P是真,要么非P是真。

二价原理进一步说明,一个陈述只有真假两种价值,不可能既真又假,也不可能既非真亦非假。

中间定律关注一个陈述与其否定的关系,二价原理则确立了陈述真假二分的原理。

两者都是经典逻辑学的基本原理。

克里特岛骗子，约公元前600年

那是克里特岛炎热的一天，哲学家埃皮门尼德斯在恶作剧。他找到了一种用逻辑证明某事的方法，嗯，不应该用逻辑来证明。

另外，在那些日子里，他不需要通过同行评审，也不需要在假期里做无薪的研究助理。下面是一张Epimenides与盆栽植物分享他的哲学发现的照片。

“啊，是的，普兰特先生。我唯一真正的伴侣'

‘All Cretans are liars. Merely by making this statement, I have deduced that that not all Cretans are liars!'

“所有的克里特人都是说谎者。仅仅通过做出这一陈述,我便推断出不是所有的克里特人都是说谎者!”

他对着他的盆栽说。在这里，我们所说的骗子是指从不说实话的人。

那么，如果他的说法是真的呢？然后我们有一个矛盾，因为这是一个说实话的克里特岛人。

被排斥的中间法则现在突然出现。该定律规定，陈述要么为真，要么否定其为真。我们刚刚表明该陈述不可能是真的（因为会有矛盾）。

等待一秒钟。当然，是否所有克里特人都是骗子是历史学家和考古学家判断的问题，而不是我们仅从逻辑中推断的问题？

这确实是一个有趣的超级大国。（如果你想更详细地了解这个悖论，见尾声II）

除非。。。也许我们在《被排除的中间人法则》中做出了一个错误的假设。也许还有其他选择。但稍后会详细介绍。

关于逻辑的微妙之处 有两个逻辑定律经常被混为一谈。

The Law of the Excluded Middle: a statement is true or its negation is true Principle of Bivalence: every statement is either true or false

外延律:一个语句要么是真的,要么它的否定是真的。 二值律:每个语句要么是真,要么是假

考虑掷骰子。“我会掷出一个6”，这句话（不一定）是真的或假的：

它是概率性的。所以二价原理失败了。

但LEM认为：“我会掷6或我不会掷6”的说法是正确的陈述。

数学基础的震颤

如果你是一个数学家，这应该敲响警钟。

排除中间定律对数学来说非常重要。正如希尔伯特——一位真正伟大的数学家——所说，“把排除中间定律从数学家手中夺走，就像拒绝天文学家使用望远镜或拳击手使用他的拳头一样”。

在数学中，我们处理这样的抽象陈述，证明如果某事不真实，我们就存在矛盾比实际构造所讨论的事物更容易。

（严谨的）直觉主义数学的创始人布劳威尔在晚年决定，他早期在拓扑学中的发现是无效的，因为它们使用了矛盾证明。

这里有一个例子，但如果它妨碍理解更广泛的文章，请随意跳过它。我已将示例放在引号框中，以便在需要时帮助跳过。

例如，考虑一个矩形框。

你要扔飞镖，我落在盒子里。每次飞镖落地时，您都会围绕该点绘制一个半径相同的圆。例如，您可以选择 0.1 厘米的半径来绘制每个飞镖。

如果我们继续这样下去，我们如何证明在有限的投掷次数之后，我们已经用画出的圆圈覆盖了整个矩形飞镖板？

空间不足

很明显，盒子也是如此。但我们想证明它适用于任何具有某些特性的形状，技术名称为紧凑性。

这个形状甚至可能是无限维度的——试着想象它！

根据排除中间定律，证明是“简单的”。我们假设我们可以无限期地选择点。

然后，我们可以使用一个众所周知的结果，如果我们将无限数量的飞镖扔到一个紧凑的空间中，比如盒子，我们可以选择一系列任意接近的飞镖。

但这是一个矛盾，因为选择的点之间的距离超过固定半径（例如，像以前一样为 0.01）。

因此，假设这个陈述是错误的，我们得到一个矛盾。所以我们推断这个说法是正确的。

但是，如果没有被排除的中间人法则，您将如何做到这一点？

数学已经够难了，没有让它变得更难！

关于逻辑技术细节的第二个简报

另一个重要的区别是非矛盾法则和被排除中间法则之间的区别。

Law of the Excluded Middle: the statement (P or not P) is true. Law of non contradiction: (P and not P) is false.

外延律:语句“P或非P”为真。 非矛盾律:“P和非P”为假

如果你正在烤一个蛋糕，并且它已经部分煮熟了，你可能不想肯定它目前是蛋糕，但也不是说它不是蛋糕。相反，它处于某种中间状态。

因此，虽然我们不允许矛盾的事物共存，但我们并没有限制我们的类别来描述现实。我们允许我们的类别稍微模糊。

直觉主义和烤蛋糕

现在可能很清楚，逻辑问题不可避免地与烘焙有关。

这是一个谎言，它们实际上不可避免地与数学联系在一起。

以布劳威尔为首的直觉主义数学家认为，数学是由心灵构建的对象组成的。

在这里，我们看到证明

¬(¬P) (symbolically) not (not P) (in words)

¬(¬P)(符号表示) 非(非P)(文字表示)

不再是 P 的有效证明。我还没有真正建造该死的东西！

在Brouwer看来，你不能假设存在一个抽象的数学陈述领域，上面贴着真或假的标签。

如果这个神秘的领域存在（在某种意义上我们无法做出正面或反面，请参阅这篇文章），那么构建方法将是不必要的。

这有点抽象，所以让我们想象希尔伯特正在烤蛋糕。希尔伯特从气味中推断，“烤箱里没有蛋糕”的说法是错误的。

于是，他高兴地开始去叫大家吃饭，因为蛋糕已经准备好了。

但布劳威尔阻止了他，并说排除中间法则不成立。在他让每个人都狼吞虎咽地吃半生不熟的蛋糕混合物之前，他应该打开该死的烤箱，看看它是否是蛋糕。

布劳威尔承认，希尔伯特有可能是正确的，但警告说，除非我们亲眼所见，否则我们无法确定。这是我使用一些创意许可证。

布劳威尔鄙视地看了希尔伯特一眼。在他眼中,这位德国数学家正往嘴里塞着一大堆生的、没有烘烤过的蛋糕面糊,边吧唧嘴边吮吸,完全不在意桌子和地板上的混乱。

希尔伯特认为布劳威尔疯了。他会频繁地打开烤箱门检查里面是否有蛋糕,这样我们压根就烤不出蛋糕来。

还有,这面糊太甜太好吃了——“嗯,我觉得这里应该有巧克力片,你真的应该尝尝看”。

希尔伯特实际上认为布劳威尔是危险的。这是有道理的——他认为布劳威尔将永远破坏数学家制作蛋糕（证明）的能力。

直觉主义继续

你现在可以很好地理解布劳威尔对非矛盾法则很好，但不接受排除中间法则。

他否认这个抽象的数学领域，在这个领域里，事物有真或假的附着在它们身上，这导致他也否认了二价原理！

在布劳威尔的数学概念中，事物必须被构建才能存在。这是一个完全不同的数学概念，需要更多的证明。（即做出较少的假设）

这看起来很奇怪，但请记住开头的悖论，这是有道理的。将布劳威尔的数学方法应用于这个思想实验，真理是一种建设性的练习。

因此，为了证明所有克里特人都是骗子，我们必须通过检查克里特人所做的每一个陈述来“构建”证明，而我们的逻辑证明是错误的。

如果我们想给它贴上标签，我们可能会说陈述是真的、假的或不确定的。这有点像应付，因为它将问题案例标记为不确定，但似乎也为解决这种混乱提供了很好的类别。

事实证明，这正是布劳威尔所做的，这是我在编辑时偶然发现的。他使用了许多有价值的逻辑，其中有一个“尚未确定”的部分。如果你真的感兴趣，你可以阅读许多有价值的逻辑

（此外，我的外行的理解是，实验量子物理学表明“不确定”是我们所知道的现实的一部分。冯·诺依曼在他的“量子逻辑”中对此进行了形式化。

直觉主义是有道理的，但你准备好抛弃现代数学了吗？ 现在这是一个棘手的问题。因为直觉主义意味着抛弃大量非常有用的数学。

只要数学“工作正常”，即产生可以使用的结果而不会到处出现矛盾，我们就不可能做到这一点。

直觉主义的一些问题

问题在于，数学是否仅仅是心理结构，这一点还不清楚。这是一个如此基本的问题，很难看出它如何被视为一种公理，无论如何。话虽如此，构建结果的证明总是比其他证明更确定。

我的预感是，现实总是比我们的类别更混乱。布劳威尔也许是对的，矛盾证明并不总是有效的，但到处放弃它似乎是荒谬的。

至少在我们的日常生活中，对于大多数明智的陈述，经典逻辑定律成立。这就是亚里士多德创造它们的原因！

我们无法先验地知道哪些类别是正确的，所以别无选择，只能即兴创作和捏造它，在出现问题时进行调整。

使用布劳威尔的推理，正确的类别无论如何都不存在，所以选择我们的公理的这个建设性过程保持了他的方法的精神。

现实世界与数学

数学着眼于给定某些结构和公理可以进行的逻辑推论。当我们应用它时，我们才能为这些类别、操作和公理注入活力。

然后我们有了与德里达（尾声IV）的联系，当我意识到这一点时，这让我感到非常震惊，我希望它会降临到你身上。

什么是数字？

它变得复杂（然后再次变得简单）

如果你认为数字只代表世界上事物的有限、整数、正数，负数就没有多大意义。例如10只绵羊，6个孩子，3只山羊。不是-1只羊。

但是我们将负数定义为一个结构，带有运算和公理，突然间我们赋予这些运算以意义。

这个意思可能是债务的概念，也可能是倒退的想法。还是过去。或减法。

同样，负 -1 的平方根 i 看起来很抽象，好像它不存在。（我一开始是这么想的）

但是，当您将复数应用于实际情况时，您就赋予了运算意义。

例如，量子物理学中具有复数的物理现象建模，或在平面上表示复数，其中乘法对应于旋转和半径的变化。

在这里，负 1 的平方根非常有意义，因为乘法在含义和目的上已经扩展为具有旋转方面。点 i 的角度为 90 度，长度为 1。

因此，当我们将点 z 乘以 i 时，我们将其旋转 90 度，并将半径缩放 1

i² = -1，因为新角度为 90 + 90 = 180 度，新半径为 1 乘以 1。

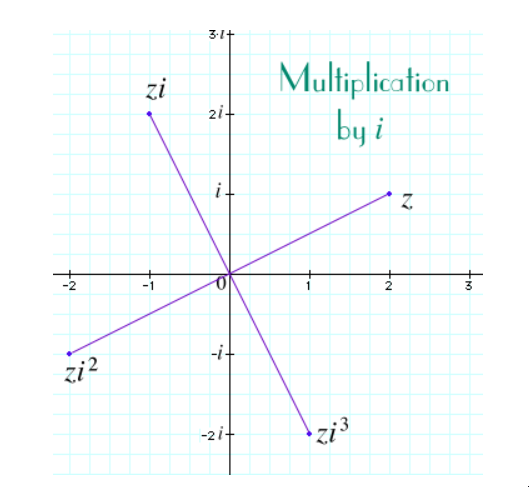
https://www2.clarku.edu/faculty/djoyce/complex/mult.html

因此，如果经典逻辑的操作在现实世界中的应用似乎是合理的，那么在数学对象上使用它们也是合理的，前提是我们限制对数学对象含义的解释领域。

数学一直专注于形式化自身内部的抽象联系，因此定义公理对现实世界的适用性也是有意义的。

因此，每当我们使用拓扑学来理解现实世界时，就会理解所需的逻辑公理。

未回答的问题

这可能会为数学的使用提供一个令人满意的答案，但是人类的好奇心呢？毕竟，数学中有一些陈述与数学中的证明有关，并且似乎由这一点定义，而不是通过应用赋予意义。

有趣的是，集合论（和测度论）中最大的问题来自集合的创建如此疯狂和疯狂，以至于很难看到与现实世界的任何相似之处。

但是，在什么意义上，一个集合，直观地是“对象的集合”，可以脱离我们对现实世界的理解，即对象似乎存在的地方？！一个失去嗅觉、味觉和触觉（所以只是一个没有外部输入的头脑）的盲人、聋哑人能够想象物体吗？

因此，数学中最抽象的部分仍然存在困境。

我想不出答案。但也许你可以。所以在评论中让我知道！如果你不能，那么无论如何在评论中让我知道。

它给了我一个借口，让我停止做我现在应该做的统计分析。尾声如下，但可选。它给出了一些最后的想法。

作者是剑桥大学经济学专业的本科生。他的爱好包括数学、哲学、亚平庸的音乐创作、制作亚平庸的双关语、手指绘画以及用第三人称写自己的简历。

尾声一 关于逻辑

如果在这里要吸取一个教训，那就是重新思考我们与逻辑的关系。

逻辑，应该是完善和形式化我们的类别和概念（如“真”和“假”）的一种方式，已经取代了它们！

这就是为什么我们在第一次试图理解排除中间定律和二价原理之间的区别时会如此困惑的原因。

我们最终将经典逻辑等同于正确的类别和看待世界的方式。如果你怀疑这两者之间的区别会令人困惑，我邀请你在哲学栈交换上阅读这篇文章。

有鉴于此，似乎很自然地出现了一些反对逻辑的阻力（咳咳，某些法国哲学家），反对捕捉所有现实的简单客观类别的想法。

但正确的反应必须是改进这些——我已经举了几个例子来说明如何——而不是把婴儿和洗澡水一起扔出去。

克里特悖论的尾声二 这个悖论与另一个悖论密切相关。这是因为问题的关键在于他，埃皮梅内德斯，是否是一个骗子。

毕竟，如果他不是骗子，那么并非所有克里特人都是骗子，因为他是克里特人。

The statement I am currently making is a lie. 我目前正在做的这个陈述是一个谎言。

尾声三：康德

我忍不住在这里对康德进行了快速的戳戳。他认为有一些不言而喻的真理，然后我们可以建立我们的知识。

但我们已经知道，这是博洛克！完全不清楚正确的假设是什么，这取决于我们从我们对世界的先入为主的知识中找出它们。

他弄错了：你必须能够假设一些知识或对世界的理解来选择和完善你的公理。

与其说完美的逻辑系统必然存在，不如说我们必须思考什么系统适合我们的需求，哪些公理是合适的。

或者，换句话说，几个世纪以来对纯粹哲学真理的追求已经死了。

但这种追求很久以前就因为其他原因而夭折了。正如尼采在《超越善恶》中所说

目前在整个欧洲处理“真实世界和表象世界”问题的急切和微妙，我甚至应该说是狡猾的，它为思考和关注提供了食粮;

而那些只在背景中听到“真理意志”而没有别的东西的人，当然不能吹嘘最敏锐的耳朵。

在极少数和孤立的情况下，这种真理的意志——某种奢侈和冒险的勇气，形而上学医生对绝望希望的野心——可能真的参与其中：

最终总是喜欢少数“确定性”而不是一大堆美好的可能性;

甚至可能有清教徒式的良心狂热分子，他们宁愿把最后的信任放在一个确定的什么都没有上，而不是一个不确定的东西上。

但那是虚无主义，是一个绝望的、致命的疲惫的灵魂的标志，尽管这种美德可能表现出勇敢的承受力。

尾声四：德里达与数学

我正在阅读一篇关于斯坦福哲学百科全书的文章，我被这种数学概念与德里达的一些想法之间的相似性所震惊。

对于德里达来说，书面标记或能指不会在自然范围内排列自己，而是形成向各个方向辐射的指链。

正如德里达的名言，“没有外部文本”（Derrida 1974 [1967]，158），也就是说，文本包括任何“内部”或“外部”之间的区别。

我不是德里达的爱好者，所以也许某个哲学系会让我成为十字准线。但这可能会敲响警钟。

纯数学就是这样——“没有外部文本”——它是一组自我指涉的能指！而且，就其本身而言，它的含义是抽象而神秘的。

我记得我问过一位数学家“空集”是什么。答案是“称为集合的数学对象，它没有元素”。真的是一套吗？这到底是什么意思？

因此，你可以采取德里德的方法，将纯数学视为从根本上自我指涉的，并应用它赋予额外的意义。

（这并不能完全满足我——数学的发展和理解总是与它的应用联系在一起。但这太令人惊讶了，不能不分享）

尾声五：自由意志、决定论和逻辑

对于那些感兴趣的人，二价原理是否始终成立与决定论有关。在前面的掷骰子示例中，也许没有不确定性，我只是缺乏相关信息。

也就是说，缺乏知识可能与二价原理的失败混为一谈。亚里士多德对此非常担心。

我认为决定论和概率思维都可以相互表述。我的一些想法在这里，这里和这里解释

P.P.P.P.S 我很抱歉我缺乏自制力！ 如果你已经走到了这一步（恭喜），几周后我可以添加一个有趣的更新。

我在数学堆栈交换上问过，事实证明，如果没有排除中间定律，某些（极其重要！）证明是无法完成的。康托尔-伯恩斯坦定理就是这样一个例子。

我的直觉是，恢复公理集将导致更少的可用证明是正确的！