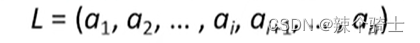有一排N个数,你和小明2个人玩游戏,每个人轮流从2端取数,每次可以从左或右取,不能从中间取。你取的所有的数的和是你的得分,小明取的所有的数的和是小明的得分。如果你先取,你最多比小明多得多少分?
输入格式
第一行:一个整数n,范围在[0, 100]。
第二行:n个整数,每个数范围在[1, 10000]。
输出格式
小明足够聪明时,你最多多得的分数。
输入/输出例子1
输入:
4
3 2 9 1
输出:
9
样例解释:
第1轮你取3;
第2轮他取2;
第3轮你取9;
第4轮他取1;
(3+9)-(2+1) = 9
样例解释
无
代码:
#include<bits/stdc++.h>
using namespace std;
int n,f[105][105],a[105],ans;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i],f[i][i]=a[i];
for(int i=1;i<=n;i++)
for(int j=1;j+i<=n;j++)
f[j][j+i]=max(-f[j+1][j+i]+a[j],-f[j][i+j-1]+a[i+j]);
cout<<f[1][n];
return 0;
}

有n个数字(0到99)排成一行,每一次可以将相邻的两个数字相加并对100取模(即除以100的余数),将结果取代之前的两个数,一次操作的花费为两个数字相乘。经过n-1次操作后剩下一个数,问剩下一个数时总花费的最小值。
输入格式
有若干组数据,每组数据第一行为一个正整数n(n<=100)表示数字的个数。
第二行为n个正整数(0到99)
输出格式
每组数据对应的最小花费。
输入/输出例子1
输入:
2
18 19
3
40 60 20
输出:
342
2400
样例解释
对于第二组数据有两种方案:
1、 先将(40和60)相加得0,再将0 和20相加得20,总花费为40*60+0*20=2400
2、 先将(60和20)相加得80,再将40和80相加得20,总花费为60*20+40*80=4400
显然第一种方案较好。
样例解释
无
代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[105],f[105][105],d[105];
int main(){
while(scanf("%d",&n)!=EOF){
for(int i = 0;i <= 105;i++){
for(int j = 1;j <= 105;j++)
f[i][j] = 1250000;
}
for(int i = 1;i <= 105;i++){
d[i] = 0;
}
for(int i = 1;i <= n;i++){
cin>>a[i];
d[i] = d[i-1]+a[i];
f[i][i] = 0;
}
for(int i = 2;i <= n;i++)
for(int j = i;j <= n;j++){
int lt = j-i+1;
for(int k = lt;k < j;k++){
int x = (d[k]-d[lt-1])%100;
int y = (d[j]-d[k])%100;
f[lt][j]=min(f[lt][j],f[lt][k]+f[k+1][j]+x*y);
}
}
cout<<f[1][n]<<endl;
}
return 0;
}- 测试
为了挽救灾区同胞的生命,心系灾区同胞的你准备自己采购一些粮食支援灾区,现在假设你一共有资金n元,而市场有m种大米,每种大米都是袋装产品,其价格不等,并且只能整袋购买。请问:你用有限的资金最多能采购多少公斤粮食呢?
输入格式
输入数据首先包含一个正整数C,表示有C(C<=10)组测试数据,每组测试数据的第一行是两个整数n和m(1<=n<=100, 1<=m<=100),分别表示经费的金额和大米的种类,然后是m行数据,每行包含3个数p,h和c(1<=p<=20,1<=h<=200,1<=c<=20),分别表示每袋的价格、每袋的重量以及对应种类大米的袋数。
输出格式
对于每组测试数据,请输出能够购买大米的最多重量,你可以假设经费买不光所有的大米,并且经费你可以不用完。每个数据的输出占一行。
输入/输出例子1
输入:
1
8 2
2 100 4
4 100 2
输出:
400
样例解释
无
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[105],b[105],c[105];
int dp[105];
int n,m;
int main()
{
int C;
scanf("%d",&C);
while(C--)
{
memset(dp, 0, sizeof(dp));
scanf("%d %d",&n,&m);
for(int i=0; i<m; i++)
{
scanf("%d %d %d",&a[i],&b[i],&c[i]);
}
for(int i=0; i<m; i++)
{
for(int j=1; j<=c[i]; j++)
{
for(int k=n; k>=a[i]*j; k--)
{
dp[k]=max(dp[k-a[i]]+b[i], dp[k]);
}
}
}
printf("%d\n",dp[n]);
}
return 0;
}有N张光盘,每张光盘有一个价钱,现在要从N张光盘中买M张,预算为L,每张光盘有一个快乐值,要求在不超过预算并且恰好买M张,使得快乐值总和最大。
输入格式
第一行为一个正整数T(1<=T<=5)表示测试数据个数
每组测试数据第一行为三个正整数N(N<=100),M(M<=N),L(L<=1000)
接下来的N行每行有两个正整数,分别是光盘的价钱与快乐值。
输出格式
每组数据对应的最大快乐值总和(保证小于2^31)。若无解则输出0.
输入/输出例子1
输入:
1
3 2 10
11 100
1 2
9 1
输出:
3
样例解释
无
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN = 1010;
const int INF = 1 << 31;
struct Movie
{
int t,v;
};
Movie movie[MAXN];
int dp[MAXN][MAXN];
int n,m,l;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&n,&m,&l);
for(int i = 1;i <= m;i++)
for(int j = 0;j <= l;j++)
dp[j][i] = -INF;
for(int j = 0;j <= l;j++)
dp[j][0] = 0;
for(int i = 1;i <= n;i++)
scanf("%d%d",&movie[i].t,&movie[i].v);
for(int i = 1;i <= n;i++)
for(int j = l;j >= movie[i].t;j--)
for(int k = m;k >= 1;k--)
dp[j][k] = max(dp[j][k],dp[j-movie[i].t][k-1]+movie[i].v);
int ans = 0;
for(int i = 1;i <= l;i++)
if(dp[i][m] > ans)
ans = dp[i][m];
printf("%d\n",ans);
}
return 0;
}总结:
状态:线性DP --?-- 区间DP
阶段:长度
阶段的方向:2种 ------ 取决于“子问题”
![[面试官,你坐好],今天我给你吹下卡顿监控](https://img-blog.csdnimg.cn/7b8ebb1464d54dd1babefb98459644e1.png)