一棵红黑树是一种特殊的二叉查找树，具有以下性质：

1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 每个叶子节点（NIL）是黑色。
4. 如果一个节点是红色的，那么它的两个儿子都是黑色的。
5. 从任意一个节点到其每个叶子节点的所有路径都包含相同数目的黑节点。

建立一棵红黑树通常需要按照以下步骤进行：
在插入数据时，一般采用插入红节点的方式，然后再通过旋转操作和颜色变换操作来维护红黑树的性质。

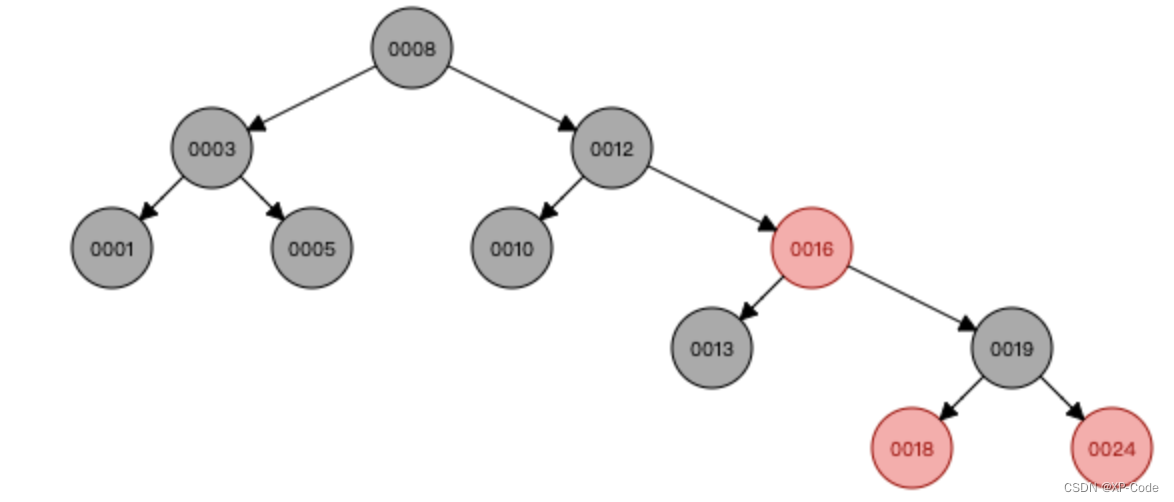
例如，下面是将整型数组[1,3,5,8,10,12,13,16,18,19,24]插入到一棵红黑树中的过程：

1.首先将1插入到树中，作为根节点。由于根节点是黑色，所以此时树满足红黑树的性质。

          1(B)

2.接下来插入3，3大于根节点1，所以插入到1的右子树中。由于插入的是红节点，且3的父节点1是黑色，所以树仍然满足红黑树的性质。

          1(B)
           \
            3(R)

3.接下来插入5，5大于根节点1，所以插入到1的右子树中。由于插入的是红节点，且5的父节点3是红节点，所以此时树不再满足红黑树的性质。为了维护性质4，需要对树进行左旋操作，将3提升为根节点。此时，3的颜色变为黑色，1的颜色变为红色。这样，树的结构就满足红黑树的性质。

          1(B)
           \
            3(R)
             \
              5(R)

旋转+变色：

          3(B)
         /   \
        1(R)  5(R)

4.接下来插入8，8大于根节点5，所以插入到5的右子树中。由于插入的是红节点，且8的父节点5是红节点，所以此时树不再满足红黑树的性质。为了维护性质4，需要对变色操作，1和5结节点都变成黑色。这样，树的结构就满足红黑树的性质。

          3(B)
         /   \
        1(B)  5(B)
        		\
        		 8(R)

5.接下来插入10，10大于根节点8，所以插入到8的右子树中。由于插入的是红节点，且10的父节点8是红节点，所以此时树不再满足红黑树的性质。为了维护性质4，需要对树进行旋转操作和变色操作。这样，树的结构就满足红黑树的性质。

          3(B)
         /   \
        1(B)  8(B)
              /   \
            5(R)	10(R)

最终得到的结果：
Red/Black Tree