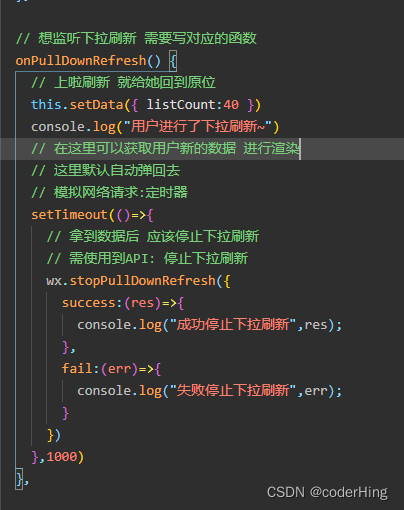
支配集

简而言之——V-支配集后剩下的点,都能在支配集中找到相邻的点
支配数的符号是γ0(有关点的集,下标为0)
例
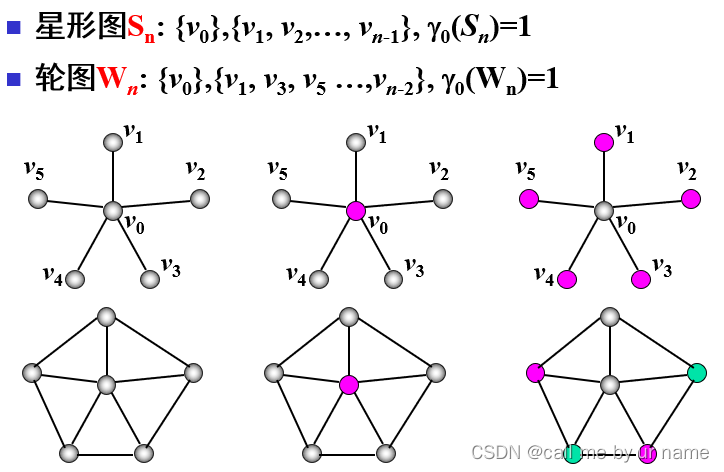
右下角相同颜色的为同一个支配集
要注意极小性
整个V就是支配集(所以说支配集找极大没有意义,只能找极小)
独立集

简而言之——在V*中每个点都是不相邻的(相互都没有边)
例
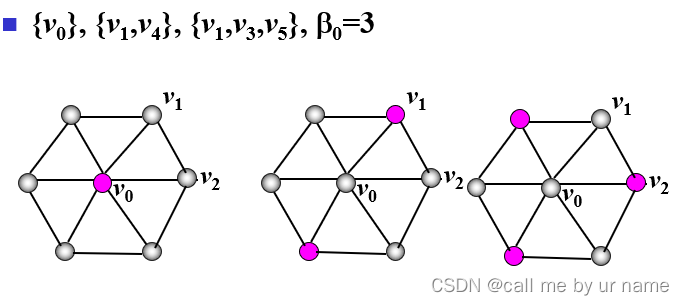
任何单个点的点集都是独立集(所以说独立集找极小没有意义,只能找极大),但是因为极大独立集的存在,所以有部分这样的独立集被覆盖
定理

证明仍是多用反证法
逆命题不成立
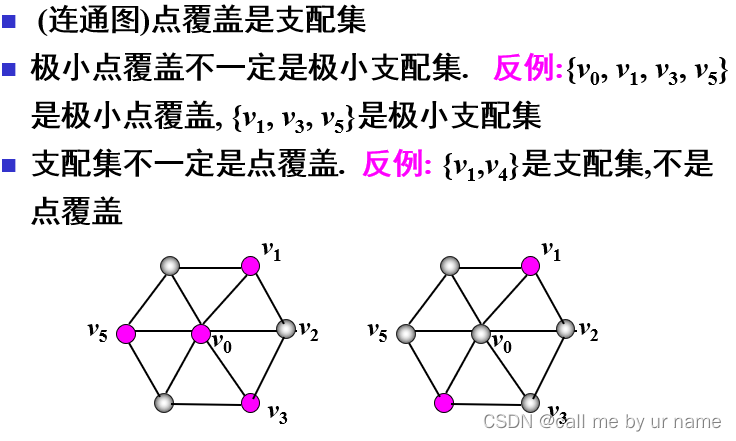
点覆盖

简而言之——V*中的点能将G中所有的边都关联上
极小性
例
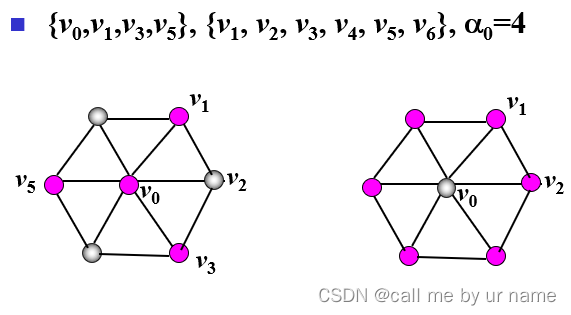
定理

等价符号↔,要证明两个:从左边到右边,从右边到左边
仍然是反证法
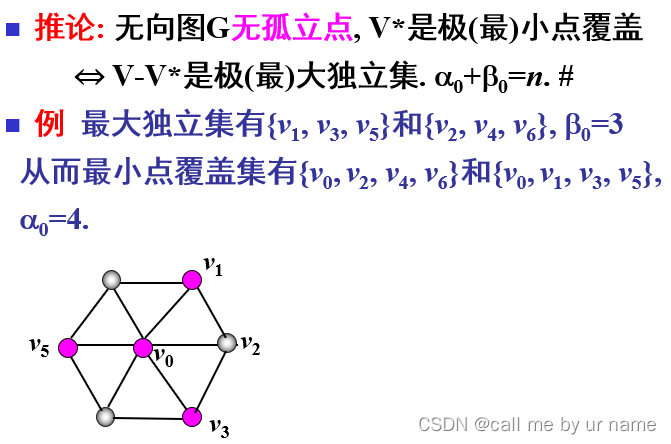
推论
团

这个知识点应该不是很重要,稍微看一下即可
例
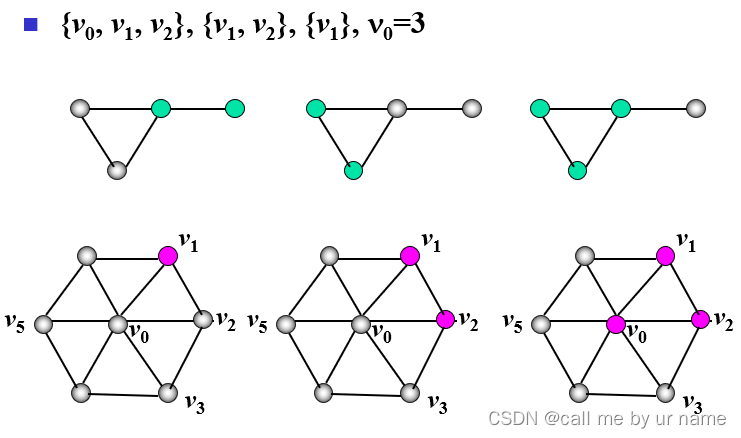
计算方法

v+与v相邻的点
a:只有b点
b:有a,b,c,所以加上a,b,c
c:有d,b

每一条边相乘一条边的2个关联点,用相加进行联系
ɑ0+β0=n

用性质:极大独立集的相对补集是极小点覆盖
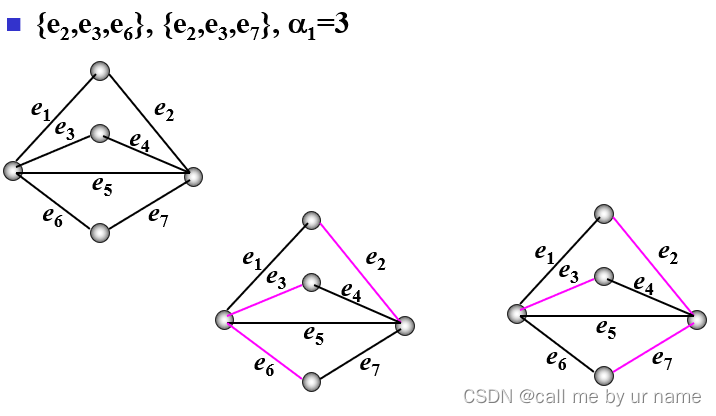
边覆盖

简而言之——E*中的边能将G中所有的点关联
例
匹配

简而言之——E*中的边互不相邻(边独立集)
例
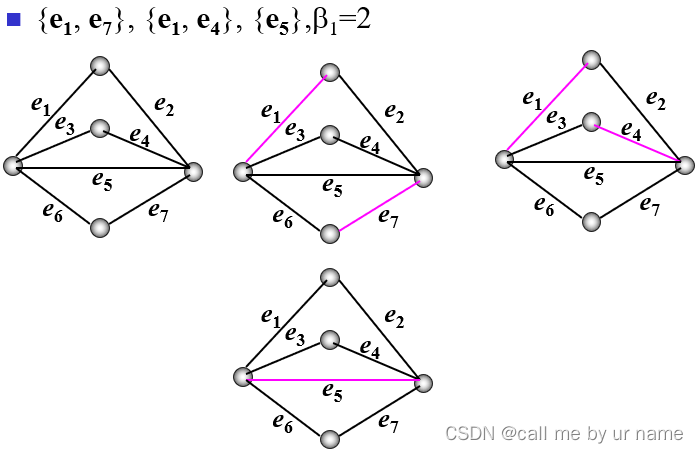
饱和点、增广路径、交错路径

饱和点——与匹配集中的边关联的点
非饱和点——不关联
一般用M代表匹配
例
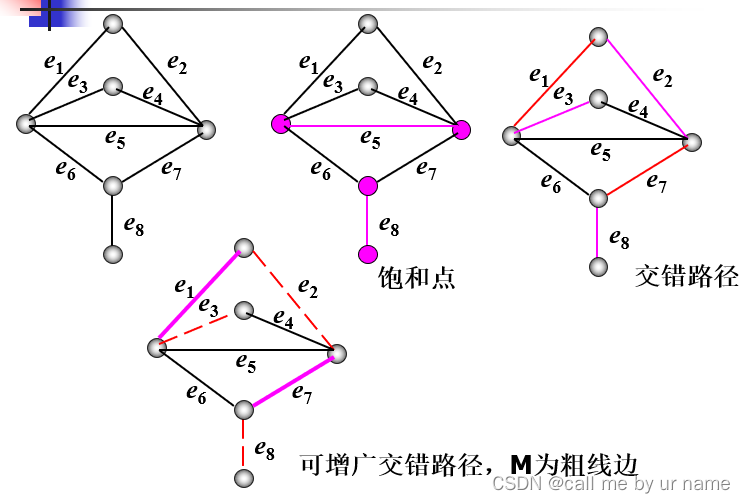
ɑ1+β1=0
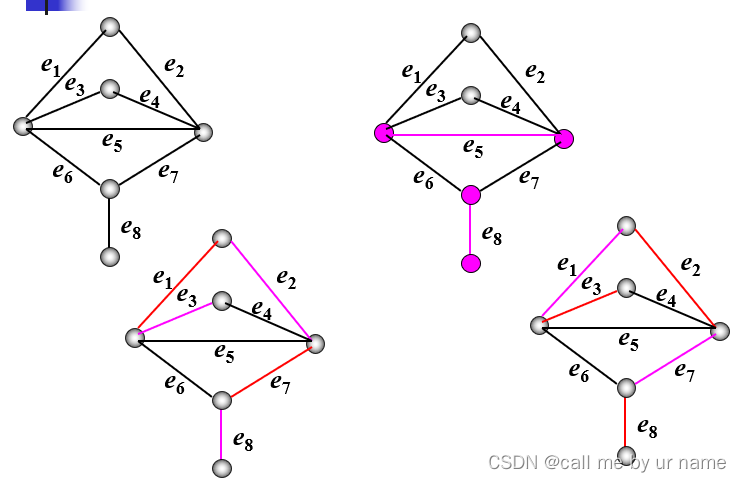
完美匹配、完备匹配
完美匹配:没有非饱和点的匹配若图中的一个匹配,包括了图中的所有点,则称这个匹配为完美匹配
完备匹配:

例
二部图的完备匹配

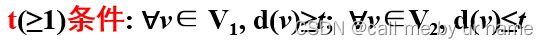


![[附源码]Python计算机毕业设计SSM基于的装修公司运营管理管理系统(程序+LW)](https://img-blog.csdnimg.cn/8da2de96ab0a46fcb98c7fd944ad7034.png)