前言：

今天我们爆刷动态规划章节的题目，相关的算法理论介绍我也有写过文章：【夜深人静学数据结构与算法 | 第十篇】动态规划_，感兴趣的可以看一看，最近家里出事了一直在忙，都没来得及刷题了。

63. 不同路径 II - 力扣（LeetCode）

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

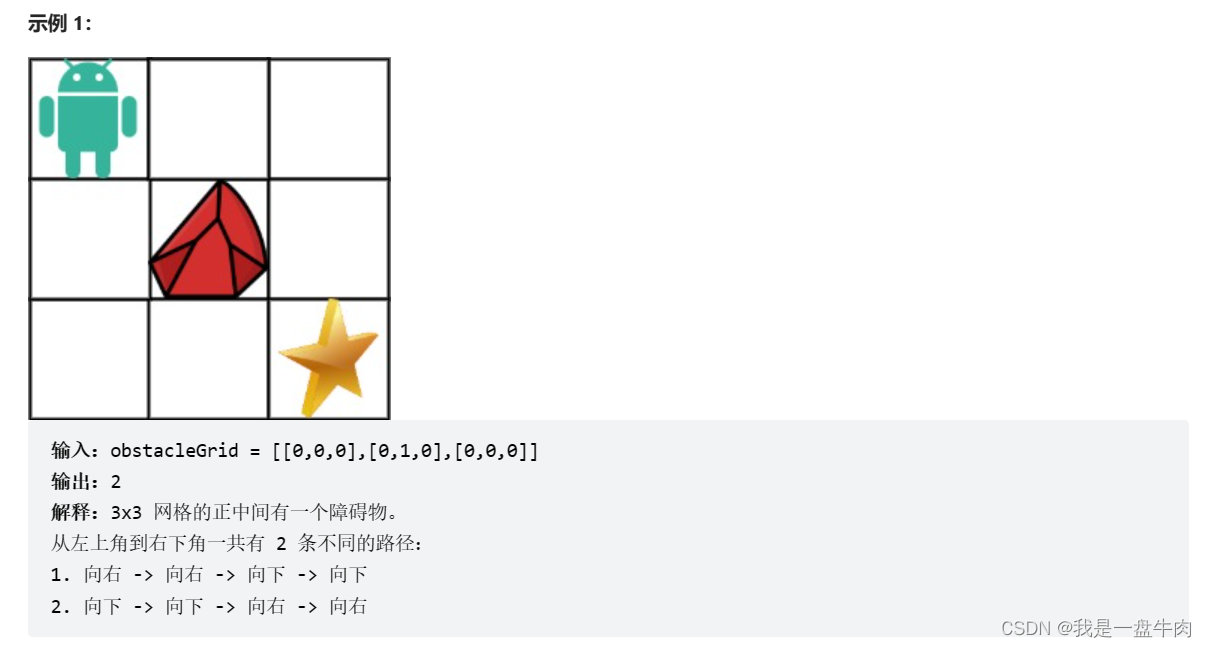
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

其实这种动态规划的题，还是严格按照我们动态规划四步走：

1.确定dp数组的含义以及下表的含义

2.递推公式的推到

3.dp数组的初始化

4.dp数组遍历顺序

那么一步一步来：

dp[i][j] 的含义就是能够到达坐标为（i，j）位置的路径条数

推导公式：本质上仍然是 dp[i][j] = dp[i-1][j] + dp[i][j-1] 。但是需要做一下微调，因为如果这个地方有障碍物了，那么就不能通过它，要不走包含这个点的路。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
           int m = obstacleGrid.size();
           int n = obstacleGrid[0].size();
        if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) 
        {
            return 0;
        }
             vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++)
        {
             dp[i][0] = 1;
        }
        
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) 
        {
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1)
                {
                    continue;
                } 
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

343. 整数拆分 - 力扣（LeetCode）

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
            }
        }
        return dp[n];
    }
};