目录
一、线性结构的定义
二、线性表的表示
三、顺序表的实现(或操作)
1、修改:
2、插入:
四、顺序表的运算效率分析:时间效率分析:
一、线性结构的定义
若结构时非空有限集,则有且仅有一个开始结点和一个终端结点,并且所有结点都最多只有一个直接前驱和一个直接后继。可表示为:(a1,a2,a3,……,an)
1,2,3,……,n:下标,即元素的序号,表示元素在表中的位置。
n为元素总个数,即表长。n>=0。当n=0时,称为 空表。
特点1、只有一个首结点和尾结点;
特点2、除首尾结点外,其它结点只有一个直接前驱和一个直接后继。
线性结构包括:线性表、堆栈、队列、字符串、数组等。其中最典型、最常用的是-----线性表。
注意:同一线性表中的元素必定具有相同特性!
二、线性表的表示
线性表的顺序表示又称为顺序存储结构或顺序映像。
顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。
特点:逻辑上相邻的元素,物理上也相邻。
顺序存储方法:用一组地址连续的存储单元一次存储线性表的元素。
例如,可以利用数组V[n]来实现。
注意:在C语言中数组的下标是从0开始的,即:V[n]的有效范围是从V[0]~V[n-1]。
三、顺序表的实现(或操作)
数据结构的基本操作: 修改、插入、删除、查找、排序
1、修改:
通过数组的下标便可访问某个特定的元素并修改之。核心语句:V[i]=x;
显然,顺序表修改操作的时间效率是O(1)。
2、插入:
在线性表的第i个位置前插入一个元素
实现步骤:(1) 将第n至第i位的元素向后移动一个位置;
(2) 将要插入的元素写到第i个位置;
(3) 表长加1。
注意:事先应判断:插入位置i是都合法?表里是否已满?
应当符合条件:1<=i<=n+1 或 i = [1,n+1]
核心语句:
for(j=n;j>=1;j--)
a[j+1]=a[j];
a[i]=x;
n++;
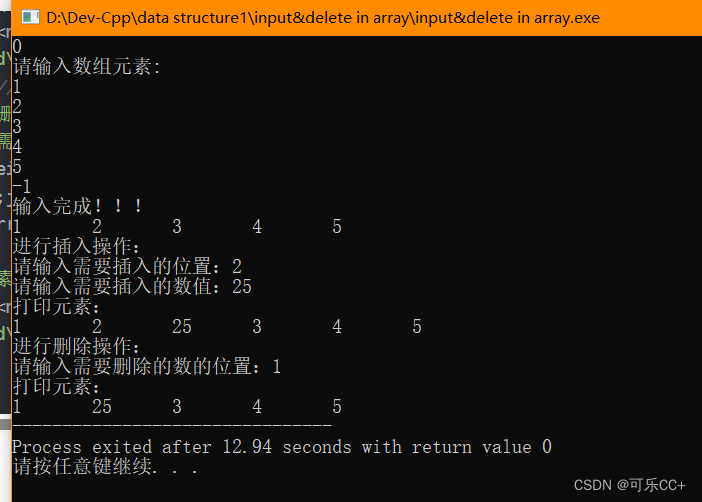
将上述插入与删除写完整:
#include <stdio.h>
#include <stdlib.h>
#define N 100
int arry[]={};
int main()
{
int num=0;
int num1=0;
int wei;
printf("%d\n",arry[num]);
printf("请输入数组元素:\n");
while(arry[num]>=0)
{
num=num1;
scanf("%d",&arry[num]);
num1++;
}
printf("输入完成!!!\n");
for(int i=0;i<num;i++)
{
printf("%d\t",arry[i]);
}
num1=0;
插入操作 num1为需要插入的数据wei,位置
printf("\n进行插入操作:\n");
printf("请输入需要插入的位置:");
scanf("%d",&wei);
if(wei<0||wei>num)
{
printf("位置输入错!!!");
exit(0);
}
else
{
printf("请输入需要插入的数值:");
scanf("%d",&num1);
for(int j=num;j>=wei;j--)
{
arry[j+1]=arry[j];
}
num++;
arry[wei]=num1;
}
printf("打印元素:\n");
for(int i=0;i<num;i++)
printf("%d\t",arry[i]);
///删除操作///wei需要删除的位置
printf("\n进行删除操作:\n");
printf("请输入需要删除的数的位置:");
scanf("%d",&wei);
for(int j=wei;j<num;j++)
arry[j]=arry[j+1];
num--;
printf("打印元素:\n");
for(int i=0;i<num;i++)
printf("%d\t",arry[i]);
return 0;
} 
四、顺序表的运算效率分析:
时间效率分析:
算符时间主要耗费在移动元素的操作上,因此计算时间复杂度的基本操作(最深层语句频度)
T(n)= o (移动元素的次数)
而移动元素的个数取决于插入或删除元素的位置。
假如:若在长度为n的线性表的第i位前插入一个元素,则向后移动元素的次数f(n)为:
f(n)= n-i+1;
若插入在尾结点之后,则根本无需移动(特别快)
若插入在首结点之前,则表中元素全部要后移(特别慢)
应当考虑各种未知插入(共n+1种可能)的平均次数才合理。
推导:假定在每个元素未知上插入x的可能性都一样。
若在首结点前插入,需要移动的元素最多,后移次数为n;
若在a(1)后面插入,则需要移动n-1个元素,后移次数为n-1;
……
若在a(n-1)后面插入,则需要移动1个元素,后移次数为1;
若在a(n)后面插入,则需要移动0个元素,后移次数为0;
所有可能的元素移动次数合计:0+1+2+……+n-1+n = (n+0)(n+1)/2
共有n+1(连头带尾)种插入形式!!!
故插入时的平均移动次数为:n(n+1))/2 ÷(n+1)=n/2≈ O(n) 【n只跟次数有关与前面的系数无关】。
同理,推导出顺序表删除一元素的时间效率为:T(n)= (n-1)/2≈O(n)。
总结:对于顺序表,插入、删除操作平均需要移动一半元素(n/2),时间的复杂度为O(n)。由于在操作时,只需要提供辅助变量,因此空间复杂度为O(1)。