一、说明

可迭代性，是数组等操作的根本；在C++程序开发过程中，可迭代操作是非常普遍、非常广泛的，然而，对这种操作知道多少，又不知道多少，都将影响开发灵活性、开发的进度。因此，本文干脆系统地全部列举这种应用，以便在使用时查阅。

二、从简单示例入手

实现数组中项的总和非常简单。我认为大多数开发人员会以这种方式实现它：

static int Sum(int[] array)
{
    var sum = 0;
    for (var index = 0; index < array.Length; index++)
        sum += array[index];
    return sum;
}

C# 中实际上有一个更简单的替代方法：

static int Sum(int[] array)
{
    var sum = 0;
    foreach (var item in array)
        sum += item;
    return sum;
}

另一种替代方法是使用 LINQ 提供的操作。它可以应用于任何可枚举项，包括数组。Sum()

那么，这三者在性能方面如何公平呢？

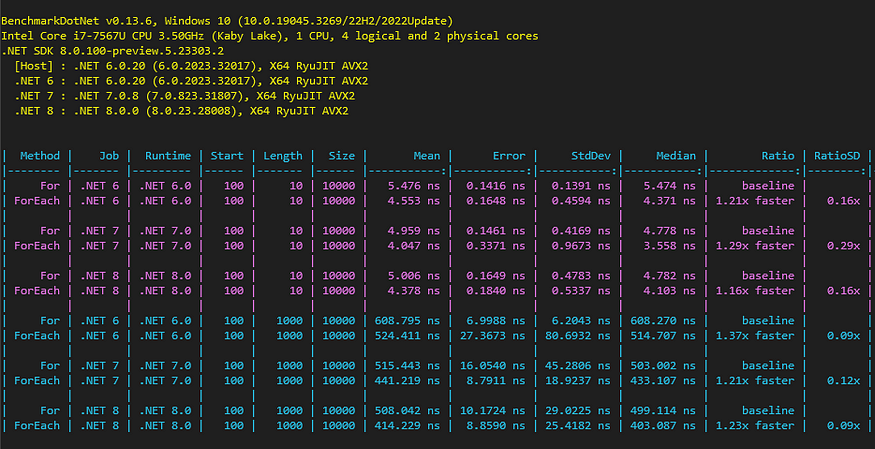
该基准测试比较了 .NET 10、1 和 000 上大小为 6 和 7.8 的阵列的性能。int

您可以看到，使用循环 比使用循环快 30% 左右 。foreachfor

在最新的 .NET 版本中，LINQ 实现有了很大的改进。它在 .NET 6 中要慢得多，但在 .NET 7 中要慢得多，对于 .NET 8 中的大型数组来说要快得多。

三、`foreachfor`

怎么能比循环更快？foreachfor和循环都是循环的语法糖。当在数组上使用这些代码时，编译器实际上会生成非常相似的代码。forforeachwhile

你可以在SharpLab中看到以下代码：

var array = new[] {0, 1, 2, 3, 4, 5 };

Console.WriteLine(Sum_For());
Console.WriteLine(Sum_ForEach());

int Sum_For()
{
    var sum = 0;
    for (var index = 0; index < array.Length; index++)
        sum += array[index];
    return sum;                     
}

int Sum_ForEach()
{
    var sum = 0;
    foreach (var item in array)
        sum += item;
    return sum;                     
}

编译器生成以下内容：

[CompilerGenerated]
private static int <<Main>$>g__Sum_For|0_0(ref <>c__DisplayClass0_0 P_0)
{
    int num = 0;
    int num2 = 0;
    while (num2 < P_0.array.Length)
    {
        num += P_0.array[num2];
        num2++;
    }
    return num;
}

[CompilerGenerated]
private static int <<Main>$>g__Sum_ForEach|0_1(ref <>c__DisplayClass0_0 P_0)
{
    int num = 0;
    int[] array = P_0.array; // copy array reference
    int num2 = 0;
    while (num2 < array.Length)
    {
        int num3 = array[num2];
        num += num3;
        num2++;
    }
    return num;
}

代码非常相似，但请注意，添加了对数组的引用作为局部变量。这允许 JIT 编译器删除边界检查，从而使迭代速度更快。检查生成的程序集的差异：foreach

Program.<<Main>$>g__Sum_For|0_0(<>c__DisplayClass0_0 ByRef)
    L0000: sub rsp, 0x28
    L0004: xor eax, eax
    L0006: xor edx, edx
    L0008: mov rcx, [rcx]
    L000b: cmp dword ptr [rcx+8], 0
    L000f: jle short L0038
    L0011: nop [rax]
    L0018: nop [rax+rax]
    L0020: mov r8, rcx
    L0023: cmp edx, [r8+8]
    L0027: jae short L003d
    L0029: mov r9d, edx
    L002c: add eax, [r8+r9*4+0x10]
    L0031: inc edx
    L0033: cmp [rcx+8], edx
    L0036: jg short L0020
    L0038: add rsp, 0x28
    L003c: ret
    L003d: call 0x000002e975d100fc
    L0042: int3

Program.<<Main>$>g__Sum_ForEach|0_1(<>c__DisplayClass0_0 ByRef)
    L0000: xor eax, eax
    L0002: mov rdx, [rcx]
    L0005: xor ecx, ecx
    L0007: mov r8d, [rdx+8]
    L000b: test r8d, r8d
    L000e: jle short L001f
    L0010: mov r9d, ecx
    L0013: add eax, [rdx+r9*4+0x10]
    L0018: inc ecx
    L001a: cmp r8d, ecx
    L001d: jg short L0010
    L001f: ret

这导致基准测试中的性能得到改善。

请注意，在 SharpLab 中，数组已经是一个局部变量，不会生成副本。在这种情况下，性能是等效的。

四、对数组进行切片

有时我们可能只想迭代数组的一部分。再一次，我认为大多数开发人员会实现以下内容：

static int Sum(int[] source, int start, int length)
{
    var sum = 0;
    for (var index = start; index < start + length; index++)
        sum += source[index];
    return sum;        
}

这可以通过使用 Span.Slice（） 方法轻松转换为 foreach：

static int Sum(int[] source, int start, int length)  
    => Sum(source.AsSpan().Slice(start, length));

static int Sum(ReadOnlySpan<int> source)
{
    var sum = 0;
    foreach (var item in source)
        sum += item;
    return sum;
}

那么，这些展会在表现方面如何呢？

在数组的一部分上使用也比使用循环好 20% 左右。foreachfor

五、LINQ

检查 in 的源代码，对于 .NET 8 之前的 .NET 版本，您会发现它使用循环。那么，如果使用 a 比 a 快，为什么在这种情况下它这么慢？Sum()System.Linqforeachforeachfor

此实现是类型的扩展方法。与和操作不同，当源在数组中时没有特殊情况。编译器将此实现转换为如下所示的内容：Sum()IEnumerable<int>Count()Where()Sum()

static int Sum(this IEnumerable<int> source)
{
    var sum = 0;
    IEnumerator<int> enumerator = source.GetEnumerator();
    try
    {
        while(enumerator.MoveNext())
            sum += enumerator.Current;
    }
    finally
    {
        enumerator?.Dispose()
    }
    return sum;
}

此代码存在多个性能问题：