定义: 队列是一种插入元素只能在一端进行, 删除元素只能在另一端进行的线性表. 所谓队列是线性表, 是指队列的逻辑结构属于线性表, 只不过在操作上加了一些约束. 队列可以插入元素的一端叫做队尾(Rear), 可以删除元素的一端叫做队头(Front). 队列是一种先进先出的结构. First In, First Out (FIFO).
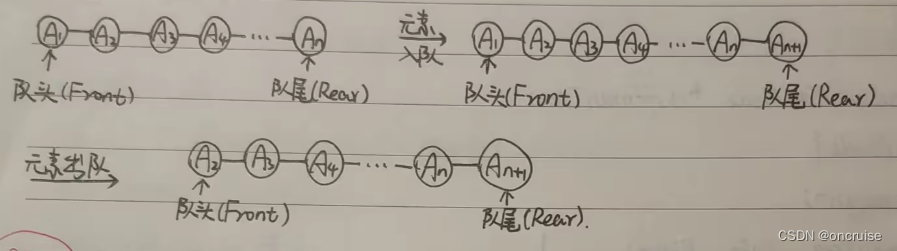
图1. 元素入队和出队
1. 顺序队列(循环队列)
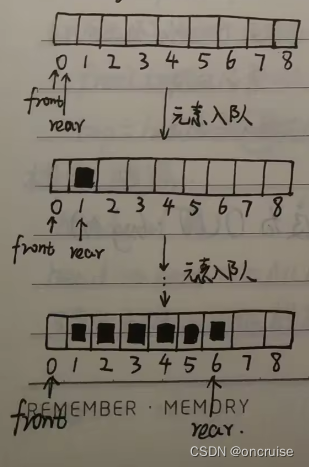
图2. 元素入队
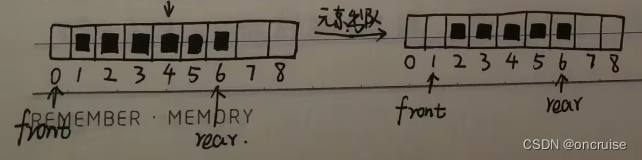
图3. 元素出队
如图, front指针指向队列首个元素的前一个位置, rear指向队列的最后一个元素. front和rear的初始值均为0. 关于入队和出队操作以及判断队空, 可以这样规定:
入队: 先移动队尾指针, 再入队元素; 即rear++; queue[ rear ] = x;
出队: 先移动队头指针, 再出队元素; 即front++; x = queue[ front ]; 元素出队后它的值还是残留在数组中的, 但已不属于队列.
队空: rear == front;
需要注意的是, 这只是一种规定, 在不同的规定下入队和出队及判断队空可能会有所不同.

图4. 假溢出
如图, rear再向后移动会造成数组越界, 但是数组内确实有空位置存在, 这种情况称为假溢出.
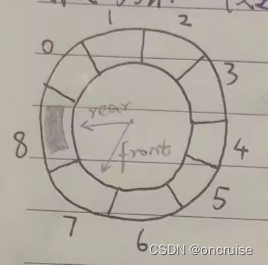
图5. 假溢出解决方法
注意, 上图只是一种演示方法, 实际上在内存中数组是不会被"掰弯"的.
如图, 定义队列queue[MAX_SIZE], front和rear初始值均为0.
入队时, 仍是先移动指针rear, 与之前不同的是, 当rear越界时, 需要让rear折返回数组的起始位置, 即rear = ( rear + 1 ) % MAX_SIZE; 然后入队元素, 即queue[ rear ] = x;
出队时, 仍时先移动指针front, 与之前不同的是, 当front越界时, 需要让front折返回数组的起始位置, 即front = ( front + 1 ) % MAX_SIZE; 然后出队元素, 即x = queue[ front ];
队空: front == rear 为真;
队满: front == ( rear + 1 ) % MAX_SIZE为真;
#include <iostream>
const int MAX_SIZE = 10;
/// <summary>
/// 队列结构体定义
/// </summary>
typedef struct {
int data[MAX_SIZE];
int front, rear;
}SqQueue;
/// <summary>
/// 初始化队列
/// </summary>
/// <param name="Q"></param>
void InitQueue(SqQueue& Q) {
Q.front = 0;
Q.rear = 0;
}
/// <summary>
/// 元素入队
/// </summary>
/// <param name="Q"></param>
/// <param name="x">入队元素</param>
void EnQueue(SqQueue& Q, int x) {
Q.rear = (Q.rear + 1) % MAX_SIZE;
Q.data[Q.rear] = x;
}
/// <summary>
/// 元素出队
/// </summary>
/// <param name="Q"></param>
/// <param name="x"></param>
void DeQueue(SqQueue& Q, int &x) {
Q.front = (Q.front + 1) % MAX_SIZE;
x = Q.data[Q.front];
}
/// <summary>
/// 判断队空, 若队空返回true, 否则返回false
/// </summary>
/// <param name="Q"></param>
/// <returns></returns>
bool QueueEmpty(SqQueue Q) {
if (Q.front == Q.rear) {
return true;
}
return false;
}
/// <summary>
/// 判断队满, 若队满返回true, 否则返回false
/// </summary>
/// <param name="Q"></param>
/// <returns></returns>
bool QueueFull(SqQueue Q) {
if (Q.front == (Q.rear + 1) % MAX_SIZE) {
return true;
}
return false;
}
int main()
{
SqQueue Q;
InitQueue(Q);
int i = 0;
while (!QueueFull(Q))
{
printf("入栈元素: %d\n", i);
EnQueue(Q, i);
i++;
}
printf("---------------------------\n");
while (!QueueEmpty(Q))
{
int x;
DeQueue(Q, x);
printf("出栈元素: %d\n", x);
}
}
代码1: 顺序队列的基本操作
运行结果如下:

图6. 运行结果
可以看出容量为10的数组在队满时只容纳了9个元素. 有一个位置没有容纳元素.
2. 链式队列
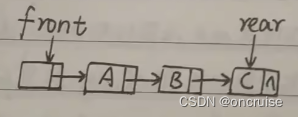
图7. 链式队列
如图, front指向链式队列的头结点, rear指向链式队列的尾结点.
入队: p指向入队结点, 注意是从队尾入队. p->next = rear->next; rear->next = p; rear = p;
出队: p指向出队结点, 注意是从队头出队. p = front->next; front->next = p->next; x = p->data; free(p);
队空: front->next == NULL为真;
队满: 假设内存足够大, 不考虑内存满的情况.
很多考题里将front和rear包在一个结构体变量里.

图8. 将front和rear包在一个结构体变量里
图中的队列没有头结点, front指向队列首个元素, 当front == NULL时, 队列为空. 为了统一操作, 我们在代码实现时设计成带头结点的单链表. 则front指向头结点, front==rear时, 队列为空.
#include <iostream>
/// <summary>
/// 链式队列结点结构体
/// </summary>
typedef struct LNode {
int data;
struct LNode* next;
}LNode;
/// <summary>
/// 链式队列
/// </summary>
typedef struct {
struct LNode* front;
struct LNode* rear;
}LinkQueue;
/// <summary>
/// 初始化队列
/// </summary>
/// <param name="Q"></param>
void InitQueue(LinkQueue& Q) {
LNode* H = (LNode*)malloc(sizeof(LNode));
H->data = NULL;
H->next = NULL;
Q.front = H;
Q.rear = H;
}
/// <summary>
/// 入队
/// </summary>
/// <param name="Q"></param>
/// <param name="x">入队元素</param>
void EnQueue(LinkQueue& Q, int x) {
LNode* p = (LNode*)malloc(sizeof(LNode));
p->data = x;
p->next = NULL;
//下面这个if()语句是不必要的, 因为Q.rear->next = p;这句代码会设置Q.front.next为p, 当然写出来也不会错
//if (Q.front == Q.rear) { //若入队前队列为空, 则先设置Q.front.next为首个入队元素
// Q.front->next = p;
//}
p->next = Q.rear->next;
Q.rear->next = p; //若入队前队列为空, 这一句会设置Q.front.next为p,
//因为队列为空时, Q.front == Q.rear == H
Q.rear = p; //这里改变了Q.rear的指向的元素, 故再次入队时,
//Q.rear->next = p;不会再改变Q.front的next的值,
//也即Q.front.next始终指向了队列首个元素
//free(p); 注意这里不能释放p所指结点的内存空间
}
/// <summary>
/// 出队
/// </summary>
/// <param name="Q"></param>
/// <param name="x">出队元素</param>
void DeQueue(LinkQueue& Q, int& x) {
LNode* p = Q.front->next;
x = p->data;
Q.front->next = p->next;
if (Q.rear == p) {
Q.rear = Q.front; //若原队列只有一个结点, 删除后变空
}
free(p);
}
/// <summary>
/// 判断队空, 队空返回true, 队不空返回false
/// </summary>
/// <param name="Q"></param>
/// <returns></returns>
bool QueueEmpty(LinkQueue Q) {
if (Q.front == Q.rear) {
return true;
}
return false;
}
int main()
{
LinkQueue Q;
InitQueue(Q);
int i = 1;
while (i < 10) {
printf("入队元素: %d\n", i);
EnQueue(Q, i);
i++;
}
printf("-----------------------------\n");
while (!QueueEmpty(Q))
{
int x;
DeQueue(Q, x);
printf("出队元素: %d\n", x);
}
}
代码2: 链式队列的基本操作

![[uni-app] 微信小程序 - 组件找不到/导入报错 (分包问题导致)](https://img-blog.csdnimg.cn/dc28d4be74d844cd831ca50d6bba6ece.png)