新版MATLAB中，图论工具箱的函数进行了更换

MATLAB中文参考文档：https://ww2.mathworks.cn/help/matlab/index.html

遍历、最短路径和循环
bfsearch 广度优先图搜索
dfsearch 深度优先图搜索
shortestpath 两个单一节点之间的最短路径
shortestpathtree 从节点的最短路径树
distances 所有节点对组的最短路径距离
allpaths 查找两个图节点之间的所有路径
maxflow 图中的最大流
minspantree 图的最小生成树
hascycles 确定图是否包含循环
allcycles 查找图中的所有循环
cyclebasis 图的基础循环基

1. 有 20 吨货物需要沿一条路径从城市1经过城市 2、3、4 运送到城市 5，可以选择3 种不同的运输方式:铁路、公路和航空匀速.在3个位于路途中间的城市里可以更改运输方式但是在相邻的两个城市之间只能采取一种运输方式，表 1给出了在每一对城市之间运输1吨货物的成本,表2 给出了在更换运输方式时每吨货物需要的额外支出,此支出与地点无关应该选择怎样的运输方案可以使得总成本最小?(提示:转化为最短路问题求解)

	1-2	2-3	3-4	4-5
铁路	30	25	40	60
公路	25	40	45	50
航空	40	20	50	45

从…装换为…	铁路	公路	航空
铁路	0	5	12
公路	8	0	10
航空	15	10	0

a = zeros(14);
a(1,2)=600;a(1,3)=500;a(1,4)=800;

a(2,5)=500;a(2,6)=900;a(2,7)=640;
a(3,5)=660;a(3,6)=800;a(3,7)=600;
a(4,5)=800;a(4,6)=1000;a(4,7)=400;

a(5,8)=800;a(5,9)=1000;a(5,10)=1240;
a(6,8)=960;a(6,9)=900;a(6,10)=1200;
a(7,8)=1100;a(7,9)=1100;a(7,10)=1000;

a(8,11)=1200;a(8,12)=1300;a(8,13)=1440;
a(9,11)=1100;a(9,12)=1000;a(9,13)=1200;
a(10,11)=1200;a(10,12)=1100;a(10,13)=900;

a(11,14)=1;a(12,14)=1;a(13,14)=1;

G = digraph(a);
plot(G)
[path1,d] = shortestpath(G,1,14);
highlight(plot(G),path1,'EdgeColor','g')
path1
d-1

3. 某市政工程公司在未来5~8 月份内需完成4 项工程:A 修建一条地下通道、B 修建一座人行天桥、C新建一条道路及 D 道路维修.工期和所需劳动力见表 1.该公司共有劳动力 120人，任一项工程在一个月内的劳动力投入不能超过 80 人，问公司如何分配劳动力完成所有工程，是否能按期完成?

工程	工期	需要劳动力（人月）
A 修建一条地下通道	5~7月	100
B 修建一座人行天桥	6~7月	80
C 新建一条道路	5~8月	200
D道路维修	8月	80

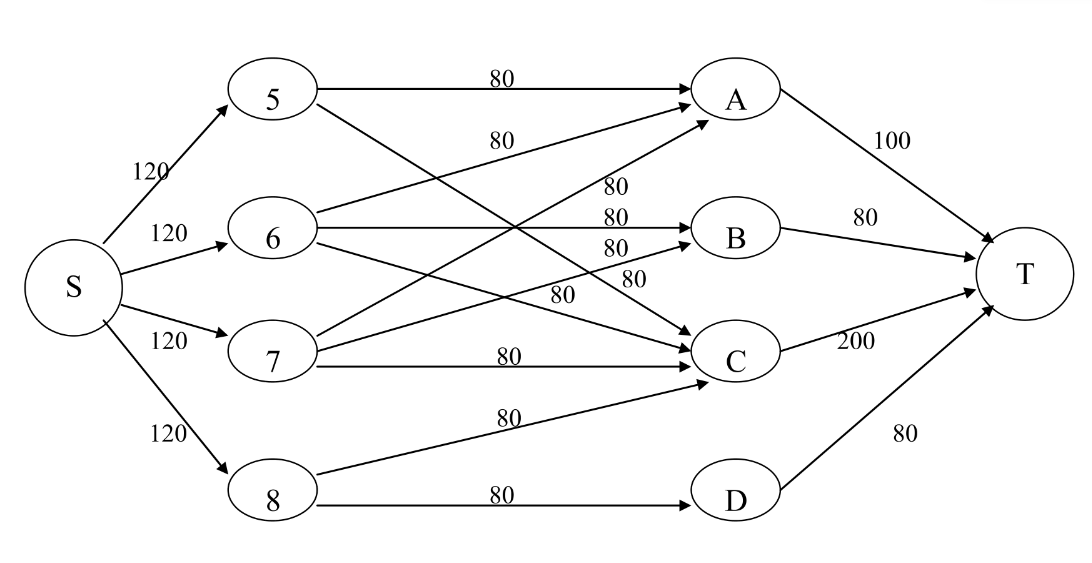
b = zeros(10);

b(1,2)=120;b(1,3)=120;b(1,4)=120;b(1,5)=120;

b(2,6)=80;b(2,8)=80;

b(3,6)=80;b(3,7)=80;b(3,8)=80;

b(4,6)=80;b(4,7)=80;b(4,8)=80;

b(5,8)=80;b(5,9)=80;

b(6,10)=100;b(7,10)=80;b(8,10)=200;b(9,10)=80;

S = digraph(b);

plot(S,'EdgeLabel',S.Edges.Weight);
[mf,GF]= maxflow(S,1,10)
GF.Edges

b = zeros(10);

b(1,2)=120;b(1,3)=120;b(1,4)=120;b(1,5)=120;

b(2,6)=80;b(2,8)=80;

b(3,6)=80;b(3,7)=80;b(3,8)=80;

b(4,6)=80;b(4,7)=80;b(4,8)=80;

b(5,8)=80;b(5,9)=80;

b(6,10)=100;b(7,10)=80;b(8,10)=200;b(9,10)=80;

S = digraph(b);

plot(S,‘EdgeLabel’,S.Edges.Weight);
[mf,GF]= maxflow(S,1,10)
GF.Edges