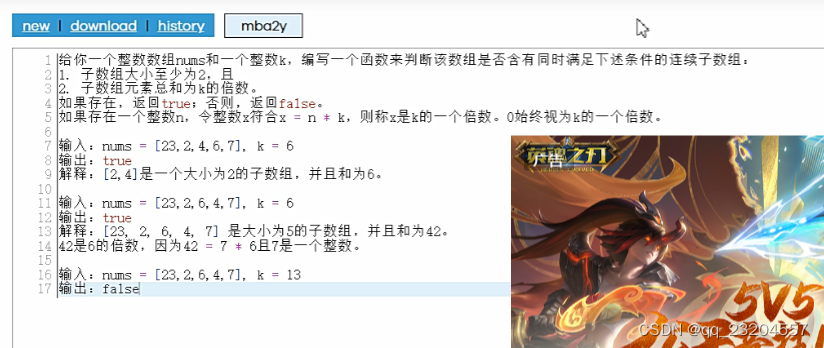
题目描述
有 七种规格的包装箱 要装到 两辆平板车 上
包装箱的宽和高是一样的
但是厚度(t 厘米)和重量(w 公斤)是不一样的
表格中给出每种包装箱的厚度、重量和数量
每辆平板车有10.2米长的地方可以用来装包装箱 像面包片一样
载重为40吨
注意:对于C5、C6、C7这三类的包装箱的总数有限制
这类的箱子所占的空间厚度不可以超过302.7厘米
要求:设计一种装车方案,使得浪费空间最少。(最大程度的利用空间)

符号说明
Xij 表示第i种规格的包装箱在第j辆平板车上的数量
然后就是:
ti 表示第i种包装箱的厚度
wi 表示第i种包装箱的重量
ni 表示第i种包装箱的数量
模型建立
目标函数:
浪费空间最少也就是最大程度使用空间
max z = 数量乘以厚度 = (求和i从1到7)ti(xi1+xi2)= (求和j从1到2)(求和i从1到7)ti*xij
约束条件:
1、件数:每种货物在装载的两辆平板车上的数量不可以超过自身的总数量
xi1 + xi2 <=ni (i从1到7)
2、厚度:每辆平板车有10.2米长的地方可以用来装包装箱,所以说总的厚度不可以超过10.2米
将米转换为厘米
10.2m = 1020cm
(求和i从1到7)ti*xij<=1020(j从1到2)
3、重量:载重为40吨
40吨 = 40000kg
(求和i从1到7)wi*xij<=40000(j从1到2)
4、注意:C5、C6、C7这三类的包装箱的总数所占的空间厚度不可以超过302.7厘米
(求和i从5到7)ti(xi1+xi2)<=302.7
5、取整:所有的货物的个数为整数
xij>=0 xij取整(i从1到7 j从1到2)

使用Lingo求解
1、将求和公式展开直接将所有项写出来
model:
max = 48.7*x11+52.0*x21+61.3*x31+72.0*x41+48.7*x51+52.0*x61+64.0*x71
+48.7*x12+52.0*x22+61.3*x32+72.0*x42+48.7*x52+52.0*x62+64.0*x72;
x11+x12<=8;
x21+x22<=7;
x31+x32<=9;
x41+x42<=6;
x51+x52<=6;
x61+x62<=4;
x71+x72<=8;
48.7*x11+52.0*x21+61.3*x31+72.0*x41+48.7*x51+52.0*x61+64.0*x71<=1020;
48.7*x12+52.0*x22+61.3*x32+72.0*x42+48.7*x52+52.0*x62+64.0*x72<=1020;
2000*x11+3000*x21+1000*x31+500*x41+4000*x51+2000*x61+1000*x71<=40000;
2000*x12+3000*x22+1000*x32+500*x42+4000*x52+2000*x62+1000*x72<=40000;
48.7*x51+52.0*x61+64.0*x71+48.7*x52+52.0*x62+64.0*x72<=302.7;
@gin(x11);@gin(x21);@gin(x31);@gin(x41);@gin(x51);@gin(x61);@gin(x71);
@gin(x12);@gin(x22);@gin(x32);@gin(x42);@gin(x52);@gin(x62);@gin(x72);
end
2、使用sum和for求解
model:
sets:
row/1..7/:t,w,n;
col/1..2/:;
matrix(row,col):x;
endsets
max=@sum(row(i):t(i)*(x(i,1)+x(i,2)));
@for(row(i):(x(i,1)+x(i,2))<=n(i));
@for(col(j):@sum(row(i):t(i)*x(i,j))<=1020);
@for(col(j):@sum(row(i):w(i)*x(i,j))<=40000);
@sum(col(j):@sum(row(i)|i#GE#5:t(i)*x(i,j)))<=302.7;
!或者写为@sum(row(i)|i#GE#5:t(i)*(x(i,1)+x(i,2))<=302.7;
@for(col(j):@for(row(i):@gin(x(i,j))));
data:
t = 48.7 52.0 61.3 72.0 48.7 52.0 64.0;
w = 2000 3000 1000 500 4000 2000 1000;
n = 8 7 9 6 6 4 8;
enddata
end
最优值为:2039.4cm



![[回馈]ASP.NET Core MVC开发实战之商城系统(一)](https://img-blog.csdnimg.cn/img_convert/0946f06ce6bea60832db40db3fc48000.png)