题目描述

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个 子集 ，并将它们堆叠起来。

如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回 堆叠长方体 cuboids 可以得到的 最大高度 。

输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。
示例 2：

输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。
示例 3：

输入：cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

提示：

n == cuboids.length
1 <= n <= 100
1 <= widthi, lengthi, heighti <= 100

求解思路

1. 这道题目类似于我们最长子序列问题和俄罗斯套娃问题，这个题目需要我们在俄罗斯套娃的基础上多考虑一个维度。
2. 首先我们先对二维数组中每一个一维子数组进行升序排序，然后再对二维数组中的元素进行排序，长相等比较宽，宽相等就比较高，保持长和宽一定的基础上，高按照降序排列，长和宽同理。
3. 枚举每一个长方体结尾的最大高度，最后循环每一个位置求得最大的值即可。

实现代码

class Solution {
    public int maxHeight(int[][] cuboids) {
        int n=cuboids.length;
        for(int i=0;i<n;i++){Arrays.sort(cuboids[i]);}
        Arrays.sort(cuboids,(a,b)->a[0]==b[0]?(a[1]==b[1]?b[2]-a[2]:b[1]-a[1]):b[0]-a[0]);
        int h[]=new int[n];
        int ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                if(cuboids[j][1]>=cuboids[i][1]&&cuboids[j][2]>=cuboids[i][2]){
                    h[i]=Math.max(h[i],h[j]);
                }
            }
            h[i]+=cuboids[i][2];
            ans=Math.max(ans,h[i]);
        }
        return ans;
    }
}

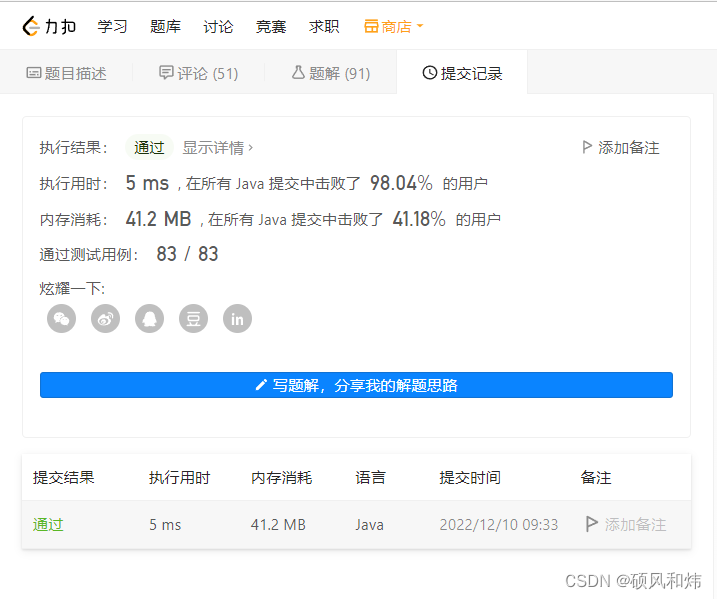
运行结果