暴力: 排序后遍历判断

class Solution {
public:
    bool isGood(vector<int> &nums) {
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size() - 1; i++)
            if (nums[i] != i + 1)
                return false;
        return nums.back() == nums.size() - 1;
    }
};

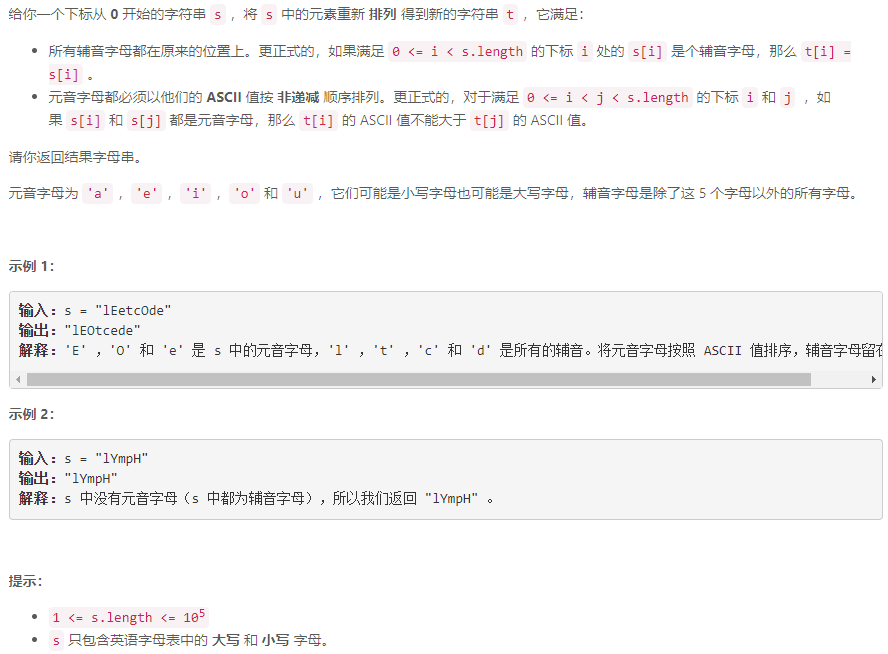
模拟: 单独对元音字母排序并对元音字母所在的位置按序赋值

class Solution {
public:
    string sortVowels(string s) {
        set<char> se{'a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'};
        vector<char> li;
        for (auto c: s)
            if (se.count(c))
                li.push_back(c);
        sort(li.begin(), li.end());
        int i = 0;
        for (auto &c: s)
            if (se.count(c))
                c = li[i++];
        return s;
    }
};

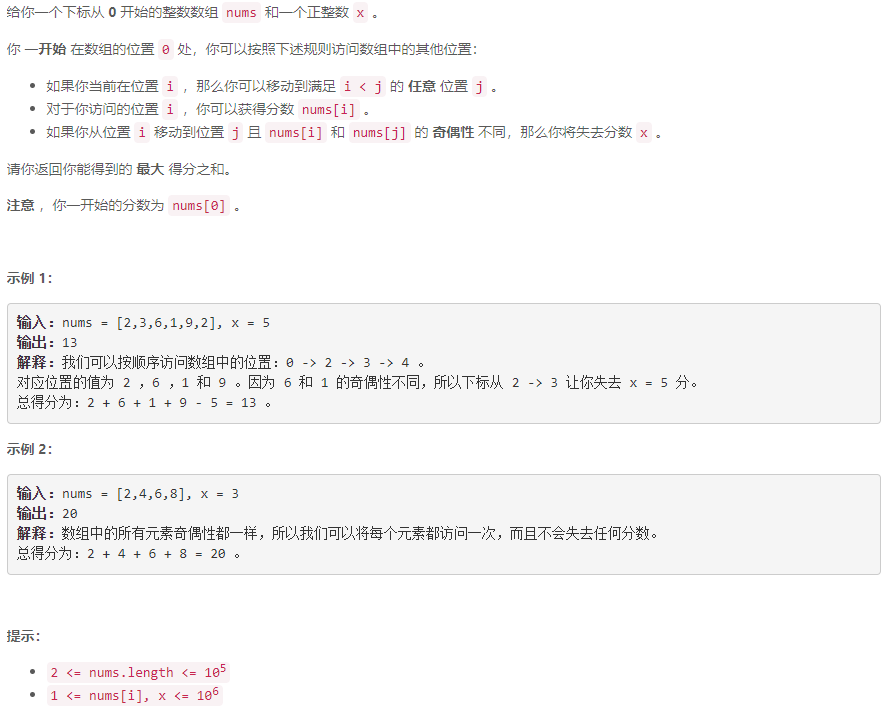
动态规划: 定义$p_{i,0}$为在$nums[0,i]$上最后一个访问的元素为偶数的最大得分和, $p_{i,1}$为在$nums[0,i]$上最后一个访问的元素为奇数的最大得分和. $p_{i,j}$的状态只与$p_{i-1,0}$和$p_{i-1,1}$有关.

class Solution {
public:
    typedef long long ll;

    long long maxScore(vector<int> &nums, int x) {
        int n = nums.size();
        ll p[n][2];
        p[0][nums[0] & 1] = nums[0];
        p[0][nums[0] & 1 ^ 1] = INT64_MIN;//无效标志
        ll res = p[0][nums[0] & 1];
        for (int i = 1; i < n; i++) {
            p[i][0] = INT64_MIN;
            p[i][1] = INT64_MIN;
            if (p[i - 1][nums[i] & 1] != INT64_MIN)
                p[i][nums[i] & 1] = max(p[i - 1][nums[i] & 1], p[i - 1][nums[i] & 1] + nums[i]);
            if (p[i - 1][nums[i] & 1 ^ 1]!= INT64_MIN)
                p[i][nums[i] & 1] = max(p[i][nums[i] & 1], p[i - 1][nums[i] & 1 ^ 1] + nums[i] - x);
            p[i][nums[i] & 1 ^ 1] = p[i - 1][nums[i] & 1 ^ 1];
            res = max({res, p[i][0], p[i][1]});
        }
        return res;
    }
};

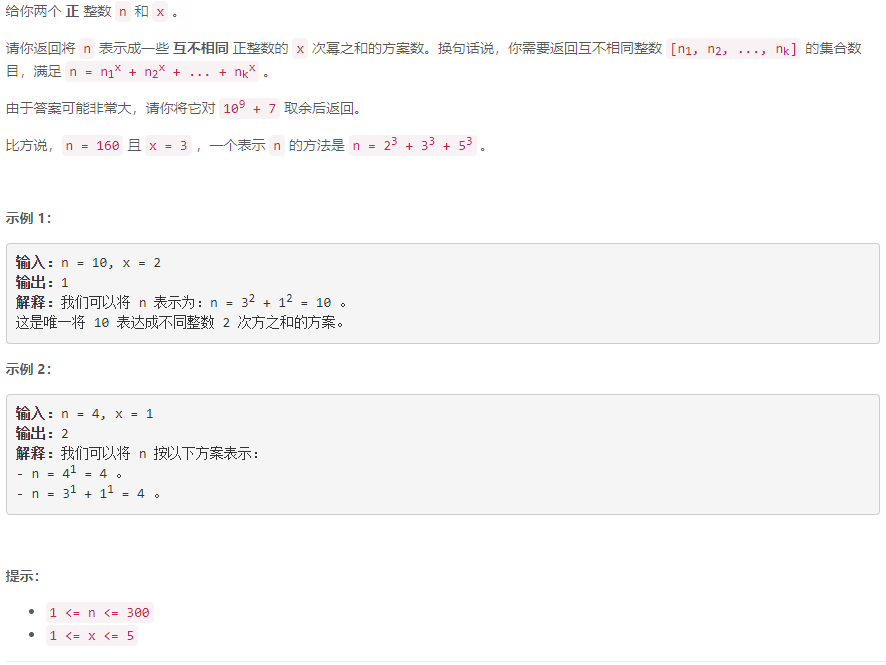
动态规划: 定义$p_{v,mx}$为将 $v$ 表示成一些互不相同且其中最大值为$mx$的正整数的 x 次幂之和的方案数. 有状态转移方程: $p_{v,mx}={\sum }_{k=0}^{mx-1}{p}_{v-m{x}^x,k}$, 实现时可以用前缀和减少计算: $s_{v,i}={\sum }_{k=0}^i{p}_{v,k}$

typedef long long ll;

ll fpow(ll x, ll n) {//快速幂: x^n
    ll res = 1;
    for (ll cur = 1, e = x; n; e = e * e, n >>= 1)
        if (n & 1)
            res *= e;
    return res;
}

class Solution {
public:
    ll mod = 1e9 + 7;

    int numberOfWays(int n, int x) {
        ll p[n + 1][n + 1];
        ll s[n + 1][n + 1];
        memset(p, 0, sizeof(p));
        memset(s, 0, sizeof(s));
        p[0][0] = 1;
        for (int i = 0; i <= n; i++)
            s[0][i] = 1;
        for (int v = 1; v <= n; v++) {
            for (int mx = 1; mx <= v && v - fpow(mx, x) >= 0; mx++)
                p[v][mx] = s[v - fpow(mx, x)][mx - 1];
            for (int i = 1; i <= n; i++)
                s[v][i] = (s[v][i - 1] + p[v][i]) % mod;
        }
        return (s[n][n] + mod) % mod;
    }
};