下一个更大元素II

给定一个循环数组, 输出每个元素的下一个更大元素, 没有则-1

所以在遍历的过程中, 模拟走了两遍nums

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int len = nums.length;
        //先进行边界判断
        if(nums == null || len <= 1){
            return new int[]{-1};
        }
        int[] res = new int[len];
        //默认初始化为-1
        Arrays.fill(res, -1);
        Stack<Integer> stack = new Stack<>();
        for(int i = 0; i < 2*len; i++){
            //这里直接使用了简单版本的写法
            //建议之后二刷的时候好好复习
            while(!stack.isEmpty() && nums[i % len] > nums[stack.peek()]){
                //还是更新res数组/弹出栈顶
                res[stack.peek()] = nums[i % len];
                stack.pop();
            }
            //还是初始化
            stack.push(i % len);
        }
        return res;
    }
}

接雨水:

这是一道很经典的题目, 并且存在三种解法

双指针解法:

首先要明确这里的雨水量需要用列来计算< 这样宽度肯定是1, 所以只要算高度就行了

每一列的雨水, 取决于左侧最高柱子和右侧最高柱子中最矮的那个高度, 减去自己柱子的高度

所以就是Min(lHeight, rHeight) - height

1. 首先遍历所有的列, 注意第一个和最后一个柱子不接雨水
2. 在for循环中求左右两边的最高柱子(每到一个柱子都遍历左右两边)

class Solution {
    public int trap(int[] height) {
        int sum = 0;
        for (int i = 0; i < height.length; i++) {
            // 第一个柱子和最后一个柱子不接雨水
            if (i==0 || i== height.length - 1) continue;

            int rHeight = height[i]; // 记录右边柱子的最高高度
            int lHeight = height[i]; // 记录左边柱子的最高高度
            for (int r = i+1; r < height.length; r++) {
                if (height[r] > rHeight) rHeight = height[r];
            }
            for (int l = i-1; l >= 0; l--) {
                if(height[l] > lHeight) lHeight = height[l];
            }
            int h = Math.min(lHeight, rHeight) - height[i];
            if (h > 0) sum += h;
        }
        return sum;

    }
}

 动态规划:

之前的双指针每到一个柱子都向左右都遍历一遍, 其实是有重复计算的, 我们把每一个位置的左边最高度记录在一个数组maxLeft上, 右边的最高高度记录在一个数组maxRight上, 这样就避免了重复计算

从左到右: maxLeft[i] = max(height, maxLeft[i - 1])

从右向左: maxRight[i] = max(height[i], maxRight[i + 1])

class Solution {
    public int trap(int[] height) {
        int length = height.length;
        if (length <= 2) return 0;
        int[] maxLeft = new int[length];
        int[] maxRight = new int[length];

        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i< length; i++){
						maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
				} 
        // 记录每个柱子右边柱子最大高度
        maxRight[length - 1] = height[length - 1];
        for(int i = length - 2; i >= 0; i--){
						 maxRight[i] = Math.max(height[i], maxRight[i+1]);
				}
        // 求和
        int sum = 0;
        for (int i = 0; i < length; i++) {
            int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
}

单调栈:

1. 单调栈的话就是用行来理解
2. 栈头到栈尾, 应该是从小到大的顺序: 一旦发现添加的柱子高度大于栈头元素, 就出现凹槽了, 栈头元素就是凹槽底部的柱子,栈头下面一个元素就是柱子左边, 添加的元素就是柱子右边
3. 遇到相同的元素, 更新栈内下标, 将栈里元素弹出, 新元素加入, 因为如果高度相同时, 我们要用右边的柱子来计算宽度

                             

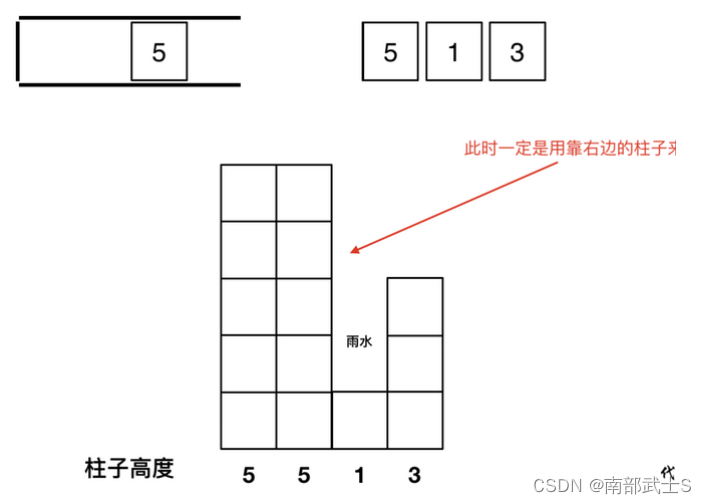
 4. 单调栈是用长*宽来计算雨水面积的, 长就是柱子的高度, 宽就是通过柱子的下标, 栈里保存int类        型的元素表示下标就行了, 到时候可以直接用stack.peek得到下标对应的高度

class Solution {
    public int trap(int[] height){
        int size = height.length;

        if (size <= 2) return 0;

        // in the stack, we push the index of array
        // using height[] to access the real height
        Stack<Integer> stack = new Stack<Integer>();
        stack.push(0);

        int sum = 0;
        for (int index = 1; index < size; index++){
            int stackTop = stack.peek();
            if (height[index] < height[stackTop]){
                stack.push(index);
            }else if (height[index] == height[stackTop]){
                // 因为相等的相邻墙，左边一个是不可能存放雨水的，所以pop左边的index, push当前的index
                stack.pop();
                stack.push(index);
            }else{
                //pop up all lower value
                int heightAtIdx = height[index];
                while (!stack.isEmpty() && (heightAtIdx > height[stackTop])){
                    int mid = stack.pop();

                    if (!stack.isEmpty()){
                        int left = stack.peek();

                        int h = Math.min(height[left], height[index]) - height[mid];
                        int w = index - left - 1;
                        int hold = h * w;
                        if (hold > 0) sum += hold;
                        stackTop = stack.peek();
                    }
                }
                stack.push(index);
            }
        }
        return sum;
    }
}