A - Exponential or QuadraticA - Exponential or Quadratic

题目大意

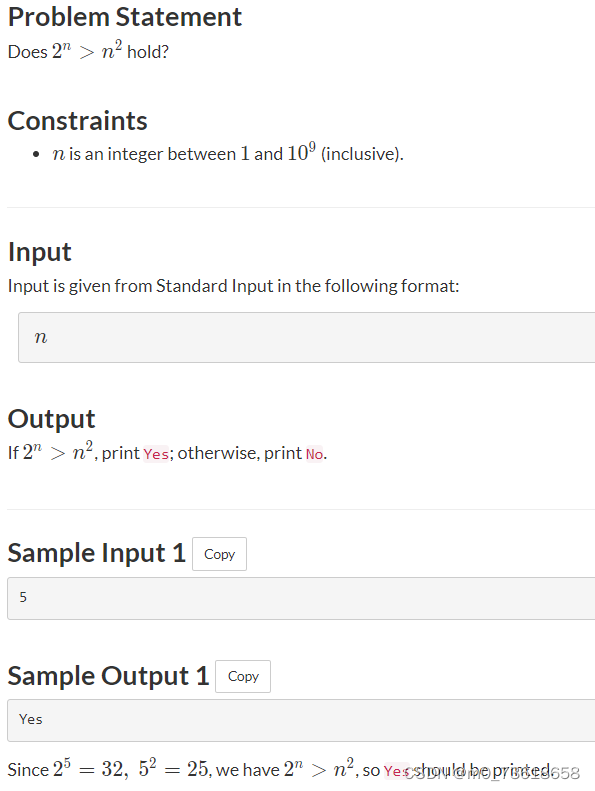
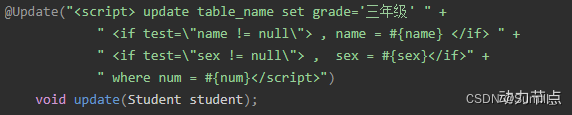
给定一个整数 n，判断是否满足 2ⁿ >n ²。

思路分析

根据数学知识可知n 的取值在 2 到 4 之间（包括 2 和 4），不满足条件。

时间复杂度

O(1)

AC代码

#include<bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;

    if (2 <= n && n <= 4) {
        cout << "No" << endl;
    } else {
        cout << "Yes" << endl;
    }

    return 0;
}

B - PizzaB - Pizza

题目大意

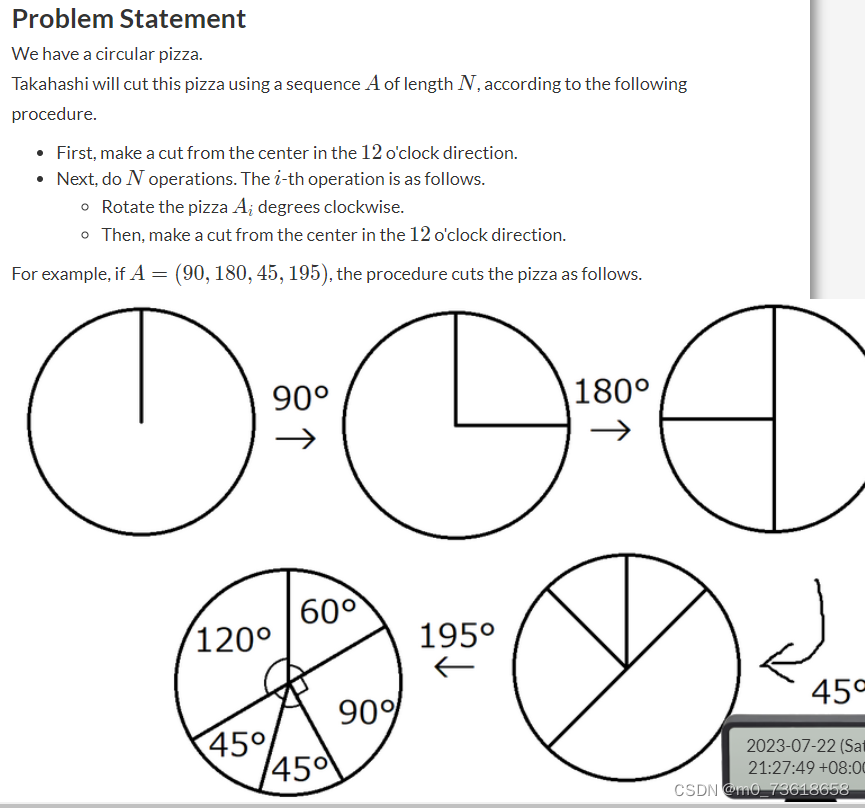
这道题目给出了一个圆形的披萨。Takahashi会按照一定的顺序切割这个披萨，切割过程如下：
首先，在12点钟方向从中心开始切割。
然后，进行N次操作。第i次操作如下：
*将披萨顺时针旋转Ai度。

在12点钟方向从中心开始切割。
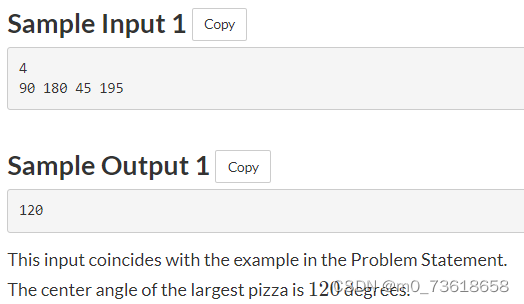
要求找到切割过程中最大披萨的中心角度。

思路分析

标记每个切口，遍历每个角度，统计每个切口（标记）之间的距离，找出最大的每个。

时间复杂度

O(n)

AC代码

#include<bits/stdc++.h>

using namespace std;

int main(){
  int n;
  cin >> n;
  
  vector<bool> fl(360,false); // 用于记录每个角度是否被切割到

  fl[0]=true; // 初始时将0度设置为已切割

  int p=0; // 当前披萨的中心角度

  for(int i=0;i<n;i++){
    int a;
    cin >> a;

    p+=a; // 更新当前披萨的中心角度
    p%=360; // 确保角度在0-359之间

    fl[p]=true; // 将当前披萨的中心角度设置为已切割
  }

  int res=0,cur=0; // res用于保存最大的中心角度值，cur用于记录当前连续未切割的角度数量

  for(int i=0;i<=360;i++){
    if(fl[i%360]){ // 如果当前角度已被切割到
      res=max(res,cur); // 更新最大中心角度值
      cur=0; // 重置连续未切割的角度数量为0
    }
    cur++; // 更新连续未切割的角度数量
  }

  cout << res << '\n'; // 输出最大中心角度值

  return 0;
}

C - digitnumC - digitnum

题目大意

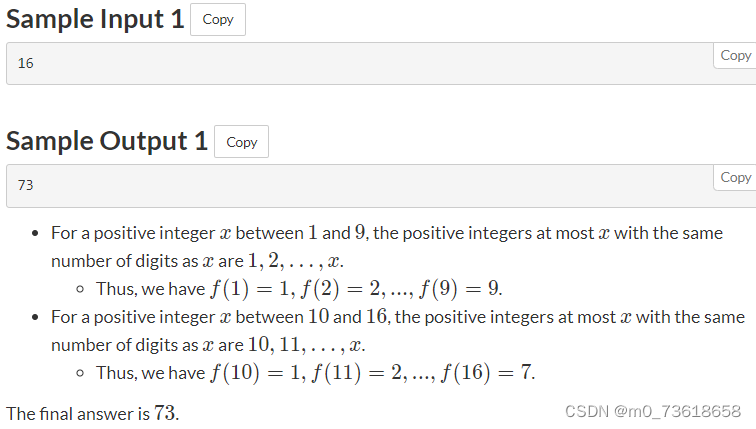
题目要求计算f(1)+f(2)+⋯+f(N)的结果，其中f(x)表示不超过x且与x位数相同的正整数的个数。需要将最终结果对998244353取模。

思路分析

通过分析题目给定的示例和问题描述，可以发现每一位上满足条件的正整数个数形成了一个三角数序列。而三角数序列有一个通项公式，可以快速计算出结果。因此，可以利用这个特性来解决问题。

知识点

三角数：通过计算三角数的性质，可以得到每一位上满足条件的正整数个数的通项公式。

时间复杂度

O(logN)

AC代码

#include<bits/stdc++.h>
#define mod 998244353
#define inv2 499122177
using ll=long long;
using namespace std;

ll triangular_number(ll x){
  x %= mod;
  ll res = x;
  res *= (x + 1);
  res %= mod;
  res *= inv2;
  res %= mod;
  return res;
}

int main() {
  ll n;
  cin >> n;
  
  ll res = 0;
  ll p10 = 10;
  for(int dg = 1; dg <= 18; dg++) {
    ll l = p10 / 10;
    ll r = min(n, p10 - 1);
    if(l <= r) {
      res += triangular_number(r - l + 1);
      res %= mod;
    }
    p10 *= 10;
  }
  
  cout << res << '\n';
  return 0;
}