原则上,pytorch不支持张量对张量的求导,它只支持标量对张量的求导
我们先看标量对张量求导的情况
import torch
x=torch.ones(2,2,requires_grad=True)
print(x)
print(x.grad_fn)
输出,由于x是被直接创建的,也就是说它是一个叶子节点,所以它的grad_fn属性的值为None
tensor([[1., 1.], [1., 1.]], requires_grad=True) None
接下来对叶子节点x进行第一步操作,y=x+2
y=x+2
print(y)
print(y.grad_fn)
输出:这里可以看到y的grad_fn属性变成了AddBackward,所以grad_fn属性记录的是该张量的上一步操作。
tensor([[3., 3.], [3., 3.]], grad_fn=) <AddBackward0 object at 0x00000206A7EE2108>
然后进行操作z=y * y * 3,再对z求平均值
z=y*y*3
out=z.mean()
print(z,out)
输出结果:
tensor([[27., 27.], [27., 27.]], grad_fn=) tensor(27., grad_fn=)
此时我们利用backward()函数来求x的梯度,由于out是求平均值得到的一个标量,所以我们可以不用向backward函数传递一个张量,而是直接计算。
out.backward()
print(x.grad)
输出:tensor([[4.5000, 4.5000], [4.5000, 4.5000]])
我们来手动计算,看得到的结果是否与backword函数得到的结果一致
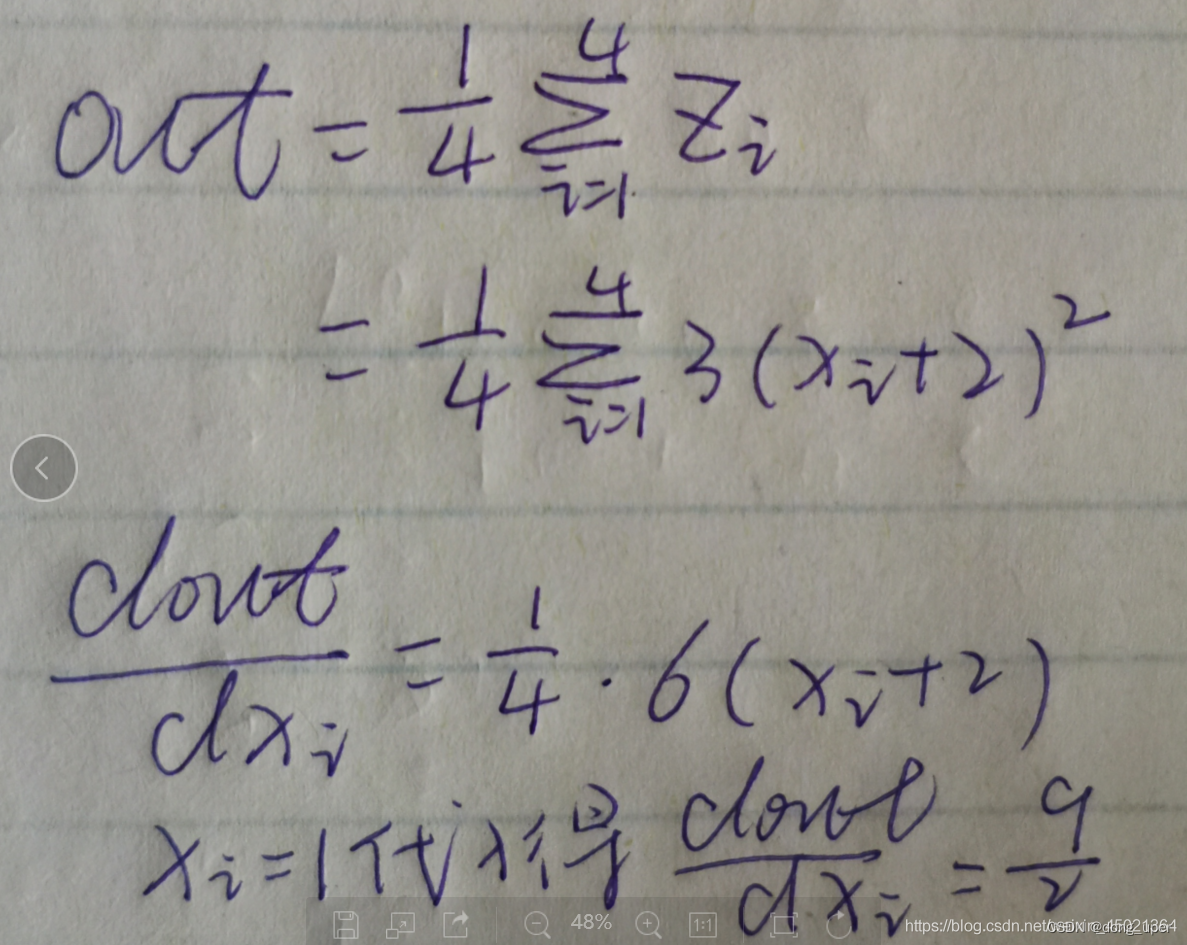
显然,结果是一致的。
再来看张量对张量求导的情况
前面已经强调过,pytorch不允许张量对张量求导,所以在使用张量对张量求导的时候,必须要传入一个与被求导张量同形的张量,然后pytorch根据传入的张量与被求导张量作加权求和将其转化为标量,这里比较晦涩难懂,没关系,接下来我们用例子来解释
首先创建一个叶子节点x
x=torch.tensor([[1.0,2.0],[3.0,4.0]],requires_grad=True)
print(x)
tensor([[1., 2.], [3., 4.]], requires_grad=True)
接下来计算y=3*x
y=3*x
print(y)
tensor([[ 3., 6.], [ 9., 12.]], grad_fn=)
接下来我们直接用y求导y.backward()
毫无意外,直接报错,这就印证了前面说过的pytorch不支持张量对张量直接求导
RuntimeError: grad can be implicitly created only for scalar outputs
于是我们构建一个与y同形的张量z,(一般是传入一个单位张量,可以参考y.backward(torch.ones_like(y)),这样计算得到的参数梯度没有张量z的影响)把z作为y.backward()的参数求y对x的导。
z=torch.tensor([[1.0,0.1],[0.01,0.001]],dtype=torch.float)
y.backward(z)
print(x.grad)
输出结果:tensor([[3.0000, 0.3000], [0.0300, 0.0030]])(张量的梯度是一个与原张量同形的张量)
事实上,到这里我们仍一头雾水,不知道这个结果是如何得出的,下面给出他的通用计算公式(需要注意的是,该公式只是用来方便计算的,属于计算技巧)
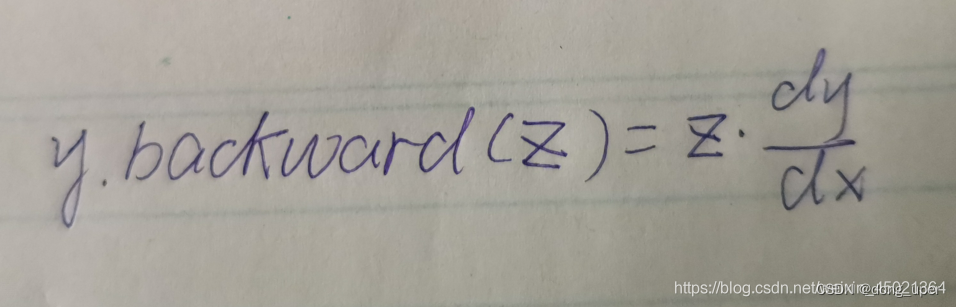
至于y对x的导数,如果有多层复合函数,利用链式法则计算即可。上面的例子比较简单,y对x求导的结果是3,再乘以张量z,很容验证得到同样的结果。
接下来我们推导上述计算公式,上文已经提到,对于表达式y.backward(z) (y、z为同形张量)的计算过程,实际上将y与z加权求和得到标量m,然后用m对x求导得到结果,也就是说实际上有这样一步计算m=torch.sum(y*z)
我们可以来验证这一步计算的正确性
m = torch.sum(y*z)
print(m)
输出tensor(3.7020, grad_fn=)可以看到的是m是一个标量。
接着再用m对x求导
m.backward()
print(x.grad)
很容易得到上述结果tensor([[3.0000, 0.3000], [0.0300, 0.0030]])
下面给出上述计算公式的推导:
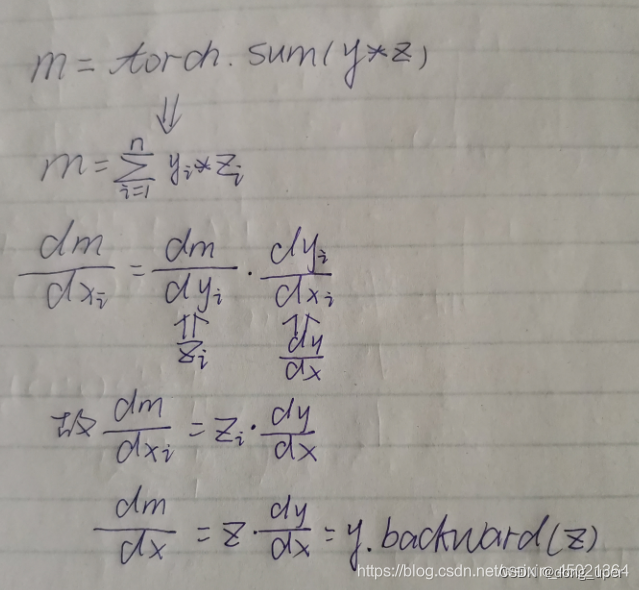
参考链接:https://blog.csdn.net/weixin_45021364/article/details/105194187