❤️ 作者简介：RO-BERRY 致力于C、C++、数据结构、TCP/IP、数据库等等一系列知识，对纯音乐有独特的喜爱
📗 日后方向 : 偏向于CPP开发以及大数据方向，如果你也感兴趣的话欢迎关注博主，期待更新

请添加图片描述

自定义类型

1.结构体
- 1.1 结构体的基础知识
- 1.2 结构体的声明
- 1.3 特殊的声明
- 1.4 结构体的自引用
- - 1.4.1 链表
1.5 结构体变量的定义和初始化
1.6 结构体内存对齐
- 1.6.1 结构体内存对齐规则
- 1.6.2 内存计算实例
- - 例1
  - 例2
  - 例3
  - 例4
1.7 修改默认对齐数
1.8 结构体传参
2. 位段
- 2.1 什么是位段
- 2.2 位段的内存分配
- 2.3 位段的跨平台问题
- 2.4 位段的应用
3. 枚举
- 3.1 枚举类型的定义
- 3.2 枚举的优点
- 3.3 枚举的使用
4. 联合（共用体）
- 4.1 联合类型的定义
- 4.2 联合的特点
- 4.3 联合大小的计算

1.结构体

1.1 结构体的基础知识

🎄结构体是一些值的集合，这些值称为成员变量。结构的每个成员可以是不同类型的变量。

1.2 结构体的声明

struct tag   结构体类型（struct）  自定义结构体名称（tag）
{
member-list;           成员列表（member-list）
}variable-list;        结构体变量列表（variable-list）

🎈我们可以定义多个结构体，我们可以给一类结构体定义一个自定义的类型名，比如说学生、教师等
我们就可以这样定义：

struct Stu            学生结构体
{
	char name[20];    名字
	int age;          年龄
	char sex[5];      性别
	char id[20];      学号
};                    分号不能丢

struct Teacher        教师结构体
{
	char name[20];    名字
	int age;          年龄
	char sex[5];      性别
};

我们想初始化变量就可以利用上面的名称
例如我们想定义学生a，学生b

定义方法1

struct Stu           
{
	char name[20];    
	int age;          
	char sex[5];      
	char id[20];      
};                    

int main()
{
	struct Stu a,b;    //定义学生a，b
}

我们也可以这样定义：
定义方法2

struct Stu            
{
	char name[20];    
	int age;          
	char sex[5];      
	char id[20];      
}a,b;                      //定义学生a，b

这两种方法定义都是可以的，效果是完全一样的
想取哪种方式取决于程序员的需求

1.3 特殊的声明

🎄在声明结构的时候，可以不完全的声明。
这种不完全声明叫做匿名结构体类型
比如:

struct
{
	int a;
	char b;
	float c;
}x;
struct
{
	int a;
	char b;
	float c;
}*p;

⭐我们在这种定义的时候，这种结构体是无法在主函数main里定义结构体变量的，我们只能采用初始化定义方式1在结构体定义的时候在尾部加入变量名，因为我们没有给这个名称自定义一个名称，无法在后面程序中定义

我们在第二个结构体中定义了结构体指针*p，而且第二个结构体的结构成员和第一个结构成员一样，那我们可不可以使p=&x呢？

我们来试一下
我们发现程序报错，并且错误如下：
在这里插入图片描述
这说明了不可以，因为我们的程序认为这两个是不同类型的结构体，虽然都是匿名结构体，而且成员列表相同，但是类型不同，无法执行操作

🍁我们以后在写结构体的时候也要注意，匿名结构体我们只能在定义上写，我们下次想用也用不了（匿名结构体的使用是很少的）

1.4 结构体的自引用

我们先来看在一个结构体里定义以自己命名的结构体会发生什么

struct Node
{
	int data;
	struct Node next;
};

我们在程序上走一走
在这里插入图片描述
🤔我们会发现不可以这样定义，错误报告说我们使用正在定义的Node,也就是我们不能在定义的时候在结构成员里使用自身

其实我们也可以发现，如果对于计算机来说。我们结构体中定义自身结构体，结构体成员里面还有结构体，这样会不停的定义，其内存是无限大，不可能停下来

可是当我们将结构体成员变成结构体指针，我们就不会报错了
比如：

struct Node
{
	int data;
	struct Node* next;
};

next是结构体指针，存的是下一个Node指针的地址，这样引用自身的定义方法，就叫做结构体的自引用

在这里我们不得不提到一个数据结构，叫做链表

1.4.1 链表

🐥定义：

链表是一种物理存储上非连续，数据元素的逻辑顺序通过链表中的指针链接次序，实现的一种线性存储结构。

🍁特点：
链表由一系列节点（链表中每一个元素称为节点）组成，节点在运行时动态生成（malloc），每个节点包括两个部分：

 一个是存储数据元素的数据域

 另一个是存储下一个节点地址的指针域

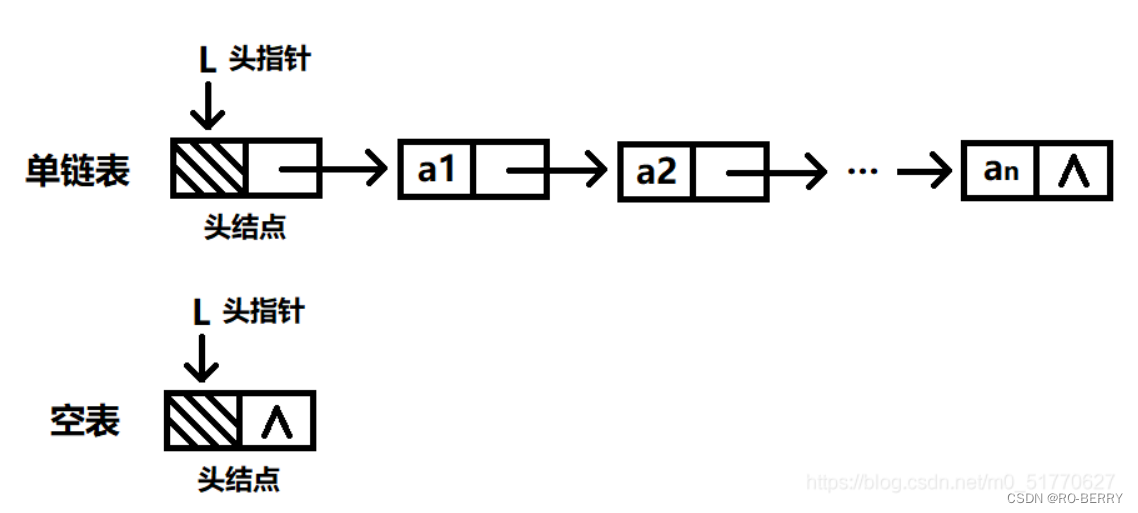
在这里插入图片描述
🎄链表的构成：
链表由一个个节点构成，每个节点一般采用结构体的形式组织，例如：

typedef struct student
｛
	 int num；                      //结点序号
	 char name[20]；                //数据内容
	 struct student *next；         //指向下一个结点的指针
 }STU;

链表中数据域存放数据，指针域指向的是下一个结点，这样便于我们访问下一个数据，而且这样存储方便修改、删除等

链表是一个很显著应用结构体的自引用的例子

接下来我们再看一例子：

typedef struct
{
	int data;
	Node* next;
	}Node;
//这样写代码，可行否？

我们可以看到，我们使用typedef将这个结构体的名字定义为Node,那么这样可以定义成功吗？

🍟答案是否定的，我们不可以在定义的时候使用结构体名，如上例，我们在定义next结构体指针的时候，编译器会去看定义这个结构体的上方是否有定义结构体Node，一看发现没有，所以就会报错

我们正确的代码应该是这样：

typedef struct Node
{
	int data;
	struct Node* next;
}Node;

1.5 结构体变量的定义和初始化

有了结构体类型，那如何定义变量，其实很简单。

struct Point
{
	int x;
	int y;
}p1; 						  //声明类型的同时定义变量p1
struct Point p2;	    	  //定义结构体变量p2
struct Point p3 = {x, y};     //初始化：定义变量的同时赋初值。
struct Stu     //类型声明
{
	char name[15];//名字
	int age;    //年龄
};
struct Stu s = {"zhangsan", 20};	//初始化
struct Node
{
	int data;
	struct Point p;
	struct Node* next;
}n1 = {10, {4,5}, NULL}; 					//结构体嵌套初始化
struct Node n2 = {20, {5, 6}, NULL};		//结构体嵌套初始化

🎄针对于不同结构体我们有不同的初始化方式，我们所有对于结构体初始化的知识，在上面代码里都有展示

1.6 结构体内存对齐

结构体内存对齐是结构体知识最难懂的点，让我们来一起学习一下。
我们知道了结构体如何定义，如何初始化，我们来思考一下，结构体里面有那么多元素，其内存是什么样的呢？

😮有人可能会说，结构体的内存大小不就是其中的元素有多少，将每个元素的大小算出来相加吗，数组里面就是元素的个数乘元素大小就得到了内存大小

答案真的是这样吗，如果这样简单就不会有人说结构体内存很难算了。
回归正题，让我们来进入结构体世界来看看到底是怎么存储的。

1.6.1 结构体内存对齐规则

🎄要想算出结构体的内存空间大小
首先得掌握结构体的对齐规则：

第一个成员存储在与结构体变量偏移量为0的地址处。
其他成员变量要对齐到某个数字（对齐数）的整数倍的地址处。
对齐数 = 编译器默认的一个对齐数与该成员大小的较小值。

VS中默认的值为8
Linux中没有默认对齐数，对齐数就是成员自身的大小

结构体总大小为最大对齐数（每个成员变量都有一个对齐数）的整数倍。
如果嵌套了结构体的情况，嵌套的结构体对齐到自己的最大对齐数的整数倍处，结构体的整
体大小就是所有最大对齐数（含嵌套结构体的对齐数）的整数倍。

为什么存在内存对齐?
大部分的参考资料都是如是说的：

平台原因(移植原因)：
不是所有的硬件平台都能访问任意地址上的任意数据的；某些硬件平台只能在某些地址处取某些特定类型的数据，否则抛出硬件异常。
性能原因：
数据结构(尤其是栈)应该尽可能地在自然边界上对齐。
原因在于，为了访问未对齐的内存，处理器需要作两次内存访问；而对齐的内存访问仅需要一次访问。

总体来说：
结构体的内存对齐是拿空间来换取时间的做法。

1.6.2 内存计算实例

😎正所谓实践是检验真理的唯一标准，我们知道了其内存对齐的规则，但是没有实际操作也是不行的，我们通过下面几个例子来学习

例1

struct S1
{
	char c1;
	int i;
	char c2;
};
printf("%d\n", sizeof(struct S1));

我们通过内存对齐规则来一个一个看：
在这里插入图片描述
我们来输出结果看看最后的内存大小是不是12

没错就是12，证明我们算的是正确的
第一次总是很艰难，我们再来多实践几次

例2

struct S2
{
	char c1;
	char c2;
	int i;
};

我们接着通过对齐规则看：
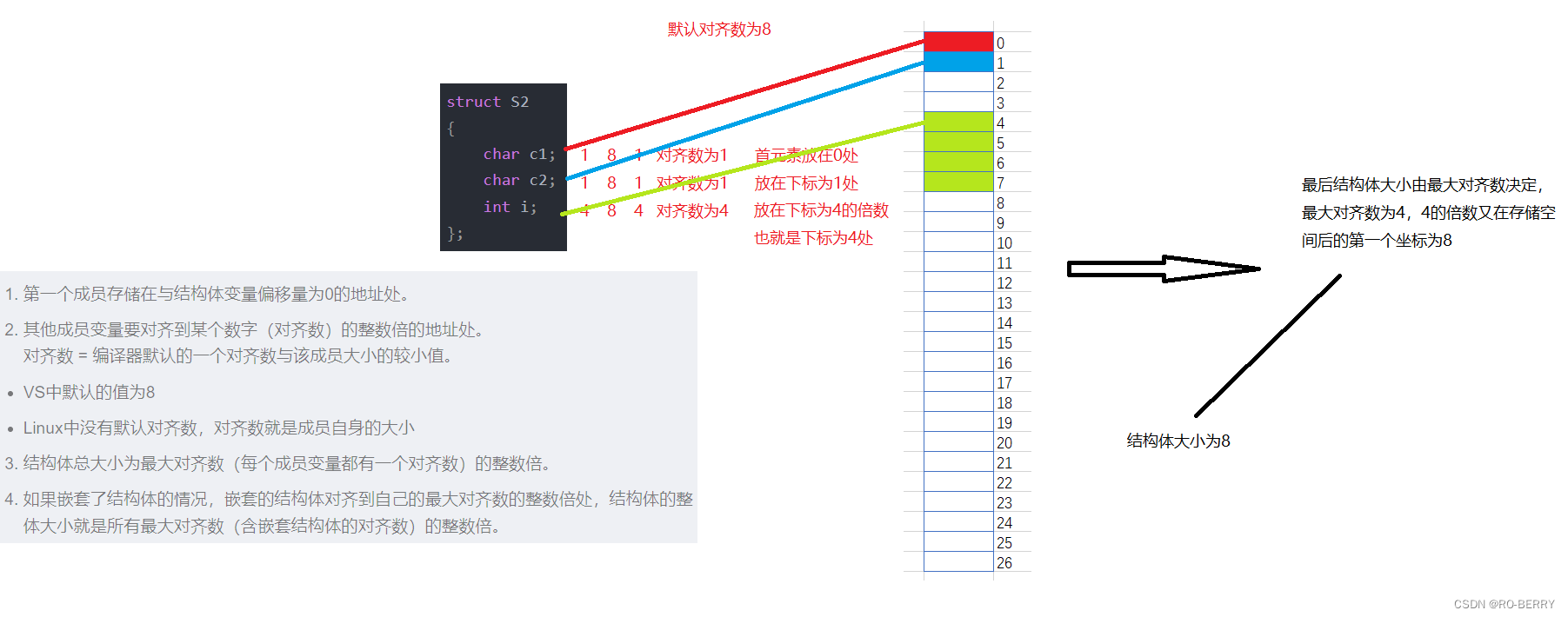
在这里插入图片描述
我们计算出结果为8
输出结果看一看是不是一致的

结果果然为8
随着我们的实践，是不是结构体内存空间的计算变的逐渐简单起来了？

例3

struct S3
{
	double d;
	char c;
	int i;
};

在这里插入图片描述

再来看在vs上的输出结果
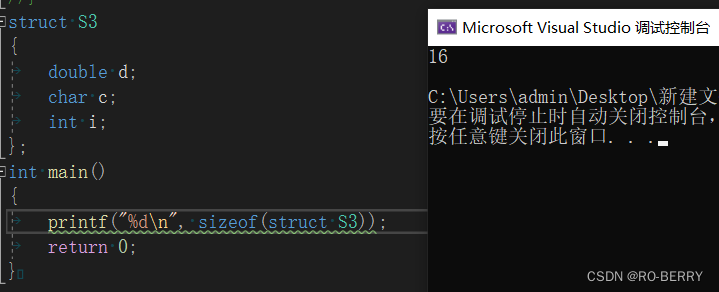
在这里插入图片描述
结果正确
是不是很简单？

例4

最后我们来看一个结构体嵌套问题，我们应该怎么求

struct S4
{
	char c1;
	struct S3 s3;
	double d;
};

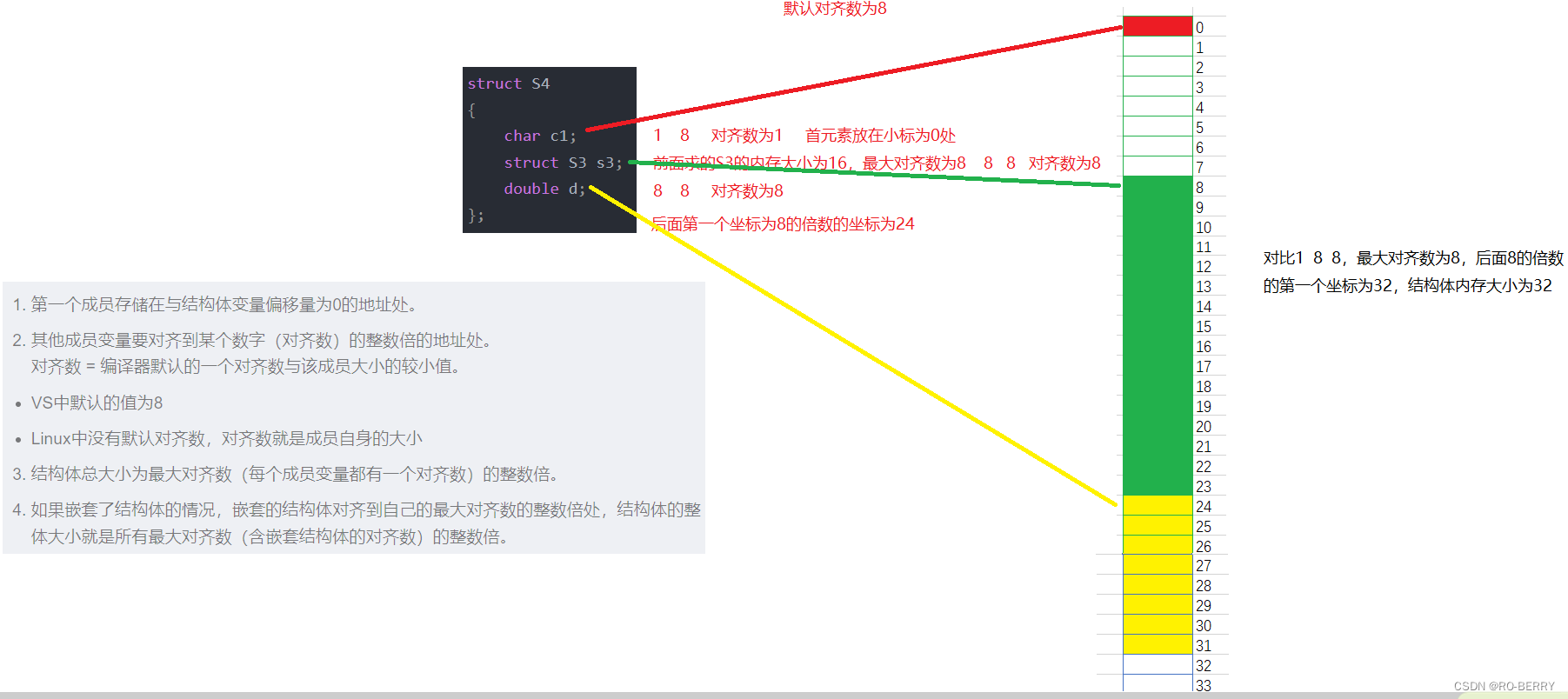
在这里插入图片描述
我们来看输出结果：

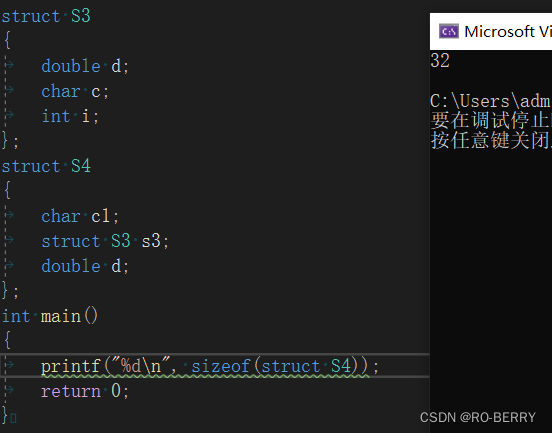
答案就是我们的32

1.7 修改默认对齐数

🐥这里介绍 #pragma 这个预处理指令，可以改变我们的默认对齐数。
我们在代码里面介绍这个用法：

#include <stdio.h>
#pragma pack(8)//设置默认对齐数为8
struct S1
{
	char c1;
	int i;
	char c2;
};
#pragma pack()//取消设置的默认对齐数，还原为默认
#pragma pack(1)//设置默认对齐数为1
struct S2
{
	char c1;
	int i;
	char c2;
};
#pragma pack()//取消设置的默认对齐数，还原为默认
int main()
{
  //输出的结果是什么？
  printf("%d\n", sizeof(struct S1));
  printf("%d\n", sizeof(struct S2));
  return 0;
}

我们可以通过上面方法的计算，这里我不再演示
通过对齐数的改变我们算出S1的大小为12，S2的大小为6
看我们的输出结果：
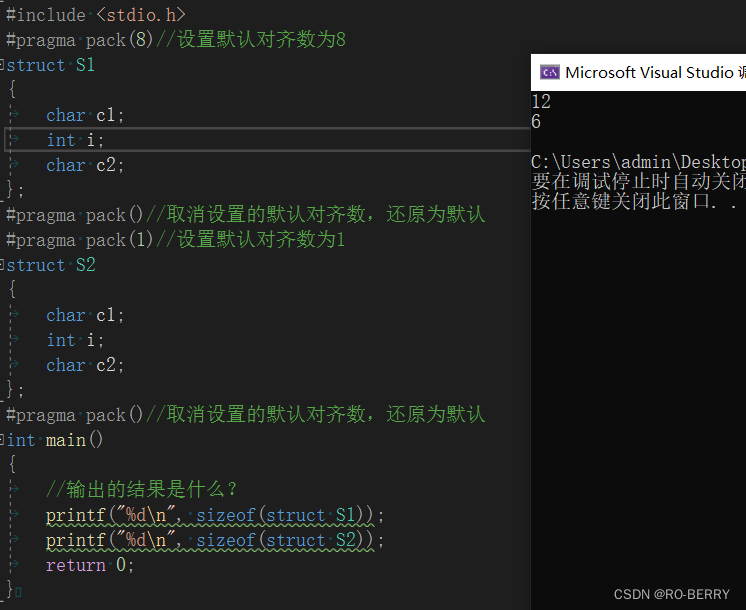
在这里插入图片描述
结果的的确确是我们改变过后算出的答案。
结论：

结构在对齐方式不合适的时候，我们可以自己更改默认对齐数。

1.8 结构体传参

直接上代码：

struct S
{
	int data[1000];
	int num;
};
struct S s = {{1,2,3,4}, 1000};
//结构体传参
void print1(struct S s)
{
	printf("%d\n", s.num);
}
//结构体地址传参
void print2(struct S* ps)
{
	printf("%d\n", ps->num);
}
int main()
{
	print1(s);  //传结构体
	print2(&s); //传地址
	return 0;
}

上面的 print1 和 print2 函数哪个好些？
答案是：首选print2函数。
原因：
函数传参的时候，参数是需要压栈，会有时间和空间上的系统开销。
如果传递一个结构体对象的时候，结构体过大，参数压栈的的系统开销比较大，所以会导致性能的下降。
🍁结论：
结构体传参的时候，要传结构体的地址。

2. 位段

🎄结构体讲完就得讲讲结构体实现位段的能力。

结构体里面我们可以发现，我们之前算过的很多结构体都是有很多的内存浪费的，因为在结构体里面我们需要考虑每个结构体成员的对齐数，在考虑了对齐数之后我们才可以进行存储，那我们如何想办法节省空间呢？
这就是位段解决的问题
🐥位段就是用来给结构体的成员给予固定的内存大小给其存储

2.1 什么是位段

位段的声明和结构是类似的，有两个不同：

1.位段的成员必须是 int、unsigned int 或signed int 。
2.位段的成员名后边有一个冒号和一个数字。

比如：

struct A
{                         //二进制
	int _a:2;             //2比特位
	int _b:5;			  //5比特位
	int _c:10;            //10比特位
	int _d:30;            //30比特位
};

A就是一个位段类型。
那位段A的大小是多少？
我们输出一下A的大小

在这里插入图片描述
输出结果为8个字节

我们口头计算一下所有成员的大小之和，2+5+10+30=47比特位
一个字节为8个比特位，那么我们需要应该需要8*6=48,6个字节才对，为什么是8个字节呢？
🍁接下来我们来看看位段是如何存储数据的：

2.2 位段的内存分配

位段的成员可以是 int unsigned int signed int 或者是 char （属于整形家族）类型
位段的空间上是按照需要以4个字节（ int ）或者1个字节（ char ）的方式来开辟的。
位段涉及很多不确定因素，位段是不跨平台的，注重可移植的程序应该避免使用位段。

//一个例子
struct S
{
	char a:3;
	char b:4;
	char c:5;
	char d:4;
};
struct S s = {0};
s.a = 10;
s.b = 12;
s.c = 3;
s.d = 4;
//空间是如何开辟的？

在这里插入图片描述
对比一下我们的答案：

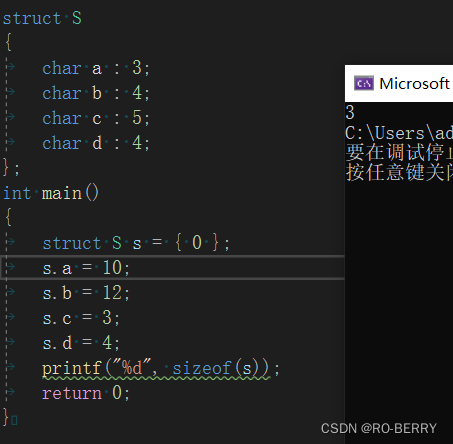
我们的计算是对的

2.3 位段的跨平台问题

int 位段被当成有符号数还是无符号数是不确定的。
位段中最大位的数目不能确定。（16位机器最大16，32位机器最大32，写成27，在16位机器会出问题。
位段中的成员在内存中从左向右分配，还是从右向左分配标准尚未定义。
当一个结构包含两个位段，第二个位段成员比较大，无法容纳于第一个位段剩余的位时是舍弃剩余的位还是利用，这是不确定的。

🎄总结：
跟结构相比，位段可以达到同样的效果，并且可以很好的节省空间，但是有跨平台的问题存在。

2.4 位段的应用

我们如果学习过计算机网络，里面讲述过IP数据报的格式
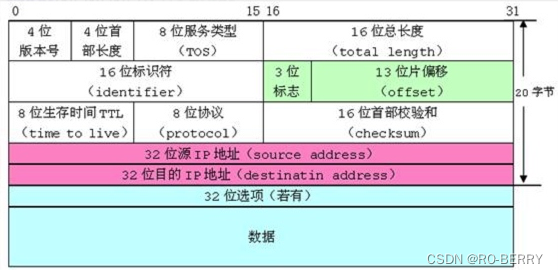
在这里插入图片描述
里面的几位几位都是用比特来做单位的，就是使用位段，才能将其中的每个部分都精确到比特位存储。
这样操作不仅仅节省空间，也节省了很多时间

3. 枚举

🐥枚举顾名思义就是一一列举。
把可能的取值一一列举。
比如我们现实生活中：
一周的星期一到星期日是有限的7天，可以一一列举。
性别有：男、女、保密，也可以一一列举。
月份有12个月，也可以一一列举
这里就可以使用枚举了。

3.1 枚举类型的定义

enum Day//星期
{
	Mon,
	Tues,
	Wed,
	Thur,
	Fri,
	Sat,
	Sun
};
enum Sex//性别
{
	MALE,
	FEMALE,
	SECRET
}；
enum Color//颜色
{
	RED,
	GREEN,
	BLUE
};

以上定义的 enum Day ， enum Sex ， enum Color 都是枚举类型。
{}中的内容是枚举类型的可能取值，也叫枚举常量。

注意

1. 每个成员变量中间需要以逗号（,）隔开
1. 如果我们没有给其中的变量赋初值的话，枚举是会从首元素开始从0开始枚举。从上往下依次递加赋值，比如：在枚举变量Day里，我们并没有给其中任何一个变量赋初值，那么Mon的值就为0，Tues的值为1，以此类推

当然在声明枚举类型的时候也可以赋初值。
例如：

enum Day//星期
{
	Mon=1,
	Tues,
	Wed,
	Thur=10,
	Fri,
	Sat,
	Sun
};

我们来依次打印每个值：
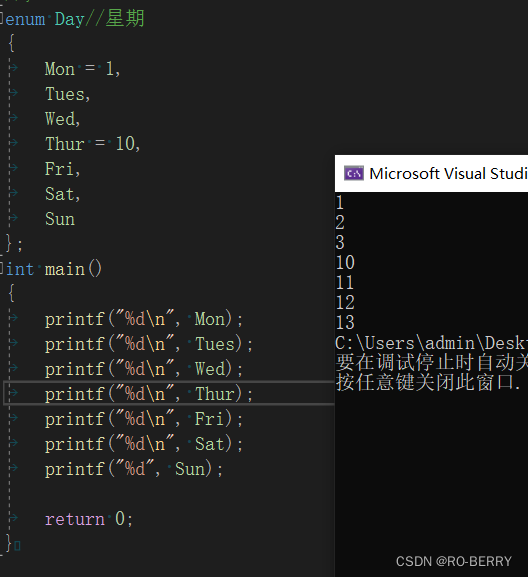
在这里插入图片描述
🎄我们可以发现，在前面的变量赋值之后，后面的变量会在其基础上进行枚举，这也是枚举的特点

3.2 枚举的优点

为什么使用枚举？
我们可以使用 #define 定义常量，为什么非要使用枚举？
🍁枚举的优点：

增加代码的可读性和可维护性
和#define定义的标识符比较枚举有类型检查，更加严谨。
便于调试
使用方便，一次可以定义多个常量

3.3 枚举的使用

enum Color//颜色
{
	RED=1,
	GREEN=2,
	BLUE=4
};
int main()
{
	enum Color cl=RED;         //枚举变量的定义，我们想给cl为RED，就定义RED，想给GREEN也可以
{

我们给cl赋值为5，这样赋值可以吗？
我们试试：

enum Color//颜色
{
	RED=1,
	GREEN=2,
	BLUE=4
};
int main()
{
	enum Color cl=5;         
{

编译器出现了报错
在这里插入图片描述
我们是不可以这样进行赋值的，只能使用枚举里的变量值

4. 联合（共用体）

4.1 联合类型的定义

联合也是一种特殊的自定义类型
🐥这种类型定义的变量也包含一系列的成员，特征是这些成员公用同一块空间（所以联合也叫共用体）。
比如：

//联合类型的声明
union Un
{
	char c;
	int i;
};
int main()
{
	//联合变量的定义
	union Un un;
	//计算这个变量的大小
	printf("%d\n", sizeof(un));
	return 0;
}

如果是结构体变量，un的大小根据内存对齐计算为8
我们来看联合体un的大小是多少
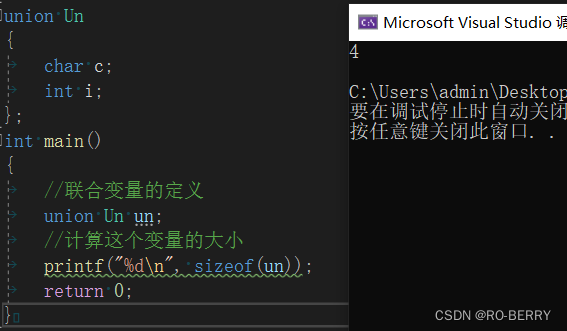
在这里插入图片描述
我们发现是4，一个char一个int加起来都有5个字节了，它的大小竟然是4😮
我们来看其中变量存储的地址为多少：

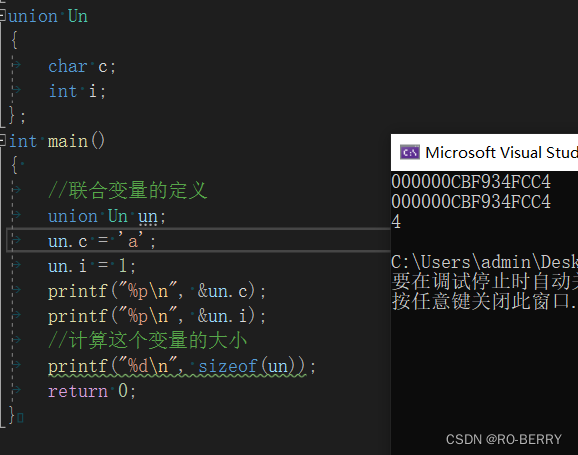
我们可以看到，联合体中两个变量使用的是同一块地址
这正是联合体的特点：
内部成员共用一块地址，彼此的改变会互相影响

4.2 联合的特点

联合的成员是共用同一块内存空间的，这样一个联合变量的大小，至少是最大成员的大小（因为联合至少得有能力保存最大的那个成员）。

union Un
{
	int i;
	char c;
};
int main()
{
	union Un un;
	// 下面输出的结果是一样的吗？
	printf("%d\n", &(un.i));
	printf("%d\n", &(un.c));
	//下面输出的结果是什么？
	un.i = 0x11223344;
	un.c = 0x55;
	printf("%x\n", un.i);
	return 0;
}

在这里插入图片描述
前面的地址一模一样我们不足为奇
可是i的十六进制我们赋值为0x11223344
输出的结果为11223355
我们的i为int类型，占4个字节，我们的c为char占一个字节，我们改变了c的值，改变了一个字节的内容，我们的i中4个字节里也有个字节的内容也被改变了，
所以输出为11223355

4.3 联合大小的计算

🎄联合的大小至少是最大成员的大小。
当最大成员大小不是最大对齐数的整数倍的时候，就要对齐到最大对齐数的整数倍。

联合的大小至少是最大成员的大小。
当最大成员大小不是最大对齐数的整数倍的时候，就要对齐到最大对齐数的整数倍。

比如：

union Un1
{
	char c[5];
	int i;
};
union Un2
{
	short c[7];
	int i;
};
//下面输出的结果是什么？
printf("%d\n", sizeof(union Un1));
printf("%d\n", sizeof(union Un2));

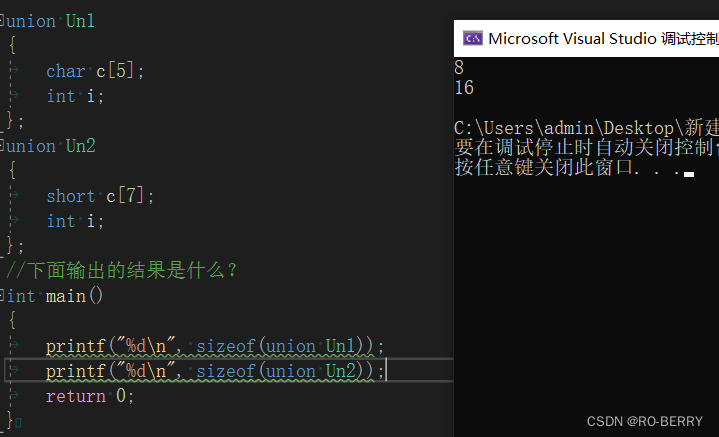
在这里插入图片描述
输出结果为8和16