文章目录
- 外点罚函数法
- 内点罚函数法
- 罚函数法 vs 拉格朗日乘子法
外点罚函数法
针对包含约束条件的最优化问题,此前介绍的拉格朗日乘子法和KKT条件已经提供一种有效的解决方案。但由于我是从智能优化算法入门运筹优化行业的,所以在遇到这类问题时,更直接的思路其实是:罚函数法。
假设原问题(P)定义如下
min
f
(
x
)
s.t.
g
i
(
x
)
≤
0
i
=
1
,
2
,
.
.
.
,
l
\text{min} \quad f(\pmb x) \\ \text{s.t.} \quad g_i(\pmb x)≤0 \quad i=1,2,...,l \\
minf(x)s.t.gi(x)≤0i=1,2,...,l
在罚函数法中,通常会构造如下的一个新问题(P1)
min
F
(
x
,
M
)
=
f
(
x
)
+
M
⋅
∑
i
=
1
l
{
m
a
x
[
g
i
(
x
)
,
0
]
}
2
\text{min} \quad F(\pmb x,M)=f(\pmb x)+M·\sum_{i=1}^l\{max[g_i(\pmb x), 0]\}^2
minF(x,M)=f(x)+M⋅i=1∑l{max[gi(x),0]}2
此处,
M
M
M为惩罚因子。
设计上式的基本思路是:当 g i ( x ) ≤ 0 g_i(\pmb x)≤0 gi(x)≤0时,约束已满足,P1目标函数中的后一项为0,P1等价于P;当 g i ( x ) > 0 g_i(\pmb x)>0 gi(x)>0时,此时不再满足约束,后一项变为 M ⋅ g i ( x ) 2 M·g_i(\pmb x)^2 M⋅gi(x)2,只要 M M M值被设置的足够大,第一项就会显著小于第二项,为了让整体最小化,迭代过程会更倾向于优先减小 g i ( x ) g_i(\pmb x) gi(x)的值,即降低约束不满足的程度,从而先将不可行解快速迭代为可行解,再逐步从可行解过渡至最优解。
当然,以上过程是通过朴素的认知推演出来的。如果要严谨一点,就需要思考,P的最优解和P1的最优解之间是怎样的关系?对 M M M的值是否有什么要求?
首先,假设P的可行域为 S S S。在可行域范围内,P和P1显然是等价的,且该结论和 M M M的取值无关。
其次,P1中的 x \pmb x x事实上并没有约束,所以其范围可以从可行域扩展到整个实数域,因为 x \pmb x x的可选范围增加了,所以P1还有机会找到更好的解,所以P≥P1。也就是说,P1为P提供了下界,即P≥P1能够取到的最大值。
然后,在P1中,如果只看
M
M
M,其系数为正,所以是单调递增的,即如果存在
M
1
<
M
2
M_1 < M_2
M1<M2,那么必然有
min
F
(
x
,
M
1
)
<
min
F
(
x
,
M
2
)
\text{min} \quad F(\pmb x,M_1) < \text{min} \quad F(\pmb x,M_2)
minF(x,M1)<minF(x,M2)
所以,当
M
→
+
∞
M\rightarrow +\infty
M→+∞时,P1取到最大值。
至此,我们可以得到结论:P1为P提供了下界,并且该下界在 M M M趋向于正无穷时取到。
举个简单的例子看一下。
min
(
x
1
−
3
)
2
+
(
x
2
−
2
)
2
s.t.
4
−
x
1
−
x
2
≥
0
\text{min} \quad (x_1-3)^2+(x_2-2)^2 \nonumber \\ \text{s.t.} \quad 4-x_1-x_2≥0 \nonumber \\
min(x1−3)2+(x2−2)2s.t.4−x1−x2≥0
以上问题中,包含2个优化变量,1个约束条件。
如果使用罚函数法,则目标函数变为
F
(
x
1
,
x
2
,
M
)
=
(
x
1
−
3
)
2
+
(
x
2
−
2
)
2
+
M
{
m
a
x
[
x
1
+
x
2
−
4
,
0
]
}
2
F(x_1,x_2,M)=(x_1-3)^2+(x_2-2)^2+M \{max [x_1+x_2-4, 0]\}^2
F(x1,x2,M)=(x1−3)2+(x2−2)2+M{max[x1+x2−4,0]}2
分开来写
F
(
x
1
,
x
2
,
M
)
=
{
(
x
1
−
3
)
2
+
(
x
2
−
2
)
2
x
1
+
x
2
−
4
≤
0
(
x
1
−
3
)
2
+
(
x
2
−
2
)
2
+
M
(
x
1
+
x
2
−
4
)
2
x
1
+
x
2
−
4
≥
0
F(x_1,x_2,M)= \begin{cases} (x_1-3)^2+(x_2-2)^2& x_1+x_2-4≤0\\ (x_1-3)^2+(x_2-2)^2+M(x_1+x_2-4)^2& x_1+x_2-4≥0 \end{cases}
F(x1,x2,M)={(x1−3)2+(x2−2)2(x1−3)2+(x2−2)2+M(x1+x2−4)2x1+x2−4≤0x1+x2−4≥0
针对每种情形,分别计算梯度
∂
F
(
x
1
,
x
2
,
M
)
∂
x
1
=
{
2
(
x
1
−
3
)
x
1
+
x
2
−
4
≤
0
2
(
x
1
−
3
)
+
2
M
(
x
1
+
x
2
−
4
)
x
1
+
x
2
−
4
≥
0
\frac{\partial F(x_1,x_2,M)}{\partial x_1}= \begin{cases} 2(x_1-3)& x_1+x_2-4≤0\\ 2(x_1-3)+2M(x_1+x_2-4)& x_1+x_2-4≥0 \end{cases}
∂x1∂F(x1,x2,M)={2(x1−3)2(x1−3)+2M(x1+x2−4)x1+x2−4≤0x1+x2−4≥0
∂ F ( x 1 , x 2 , M ) ∂ x 2 = { 2 ( x 2 − 2 ) x 1 + x 2 − 4 ≤ 0 2 ( x 2 − 2 ) + 2 M ( x 1 + x 2 − 4 ) x 1 + x 2 − 4 ≥ 0 \frac{\partial F(x_1,x_2,M)}{\partial x_2}= \begin{cases} 2(x_2-2)& x_1+x_2-4≤0\\ 2(x_2-2)+2M(x_1+x_2-4)& x_1+x_2-4≥0 \end{cases} ∂x2∂F(x1,x2,M)={2(x2−2)2(x2−2)+2M(x1+x2−4)x1+x2−4≤0x1+x2−4≥0
最优性必要条件是:梯度值为0。
如果
x
1
+
x
2
−
4
≤
0
x_1+x_2-4≤0
x1+x2−4≤0,那么
x
1
=
3
x
2
=
2
x_1=3 \\ x_2=2
x1=3x2=2
此时
x
1
+
x
2
−
4
=
1
>
0
x_1+x_2-4=1>0
x1+x2−4=1>0,与假设条件不符合,舍去。
如果
x
1
+
x
2
−
4
≥
0
x_1+x_2-4≥0
x1+x2−4≥0,那么可以得到
x
1
=
5
M
+
3
2
M
+
1
x
2
=
3
M
+
2
2
M
+
1
x_1=\frac{5M+3}{2M+1} \\ x_2=\frac{3M+2}{2M+1}
x1=2M+15M+3x2=2M+13M+2
M
→
+
∞
M\rightarrow +\infty
M→+∞时,
x
1
,
x
2
x_1,x_2
x1,x2的值可以通过洛必达法则得到
x
1
=
5
2
x
2
=
3
2
x_1=\frac{5}{2} \\ x_2=\frac{3}{2}
x1=25x2=23
此时,
x
1
+
x
2
−
4
=
0
x_1+x_2-4=0
x1+x2−4=0,符合假设条件。
另外,海森矩阵为
∇
2
F
(
x
1
,
x
2
,
M
)
=
[
∂
F
∂
x
1
2
∂
F
∂
x
1
x
2
∂
F
∂
x
2
x
1
∂
F
∂
x
2
2
]
=
[
2
M
+
2
2
M
2
M
2
M
+
2
]
\nabla^2F(x_1,x_2,M)= \begin{bmatrix} \frac{\partial F}{\partial x_1^2}&\frac{\partial F}{\partial x_1x_2}\\ \frac{\partial F}{\partial x_2x_1}&\frac{\partial F}{\partial x_2^2} \end{bmatrix}= \begin{bmatrix} 2M+2&2M\\ 2M&2M+2 \end{bmatrix}
∇2F(x1,x2,M)=[∂x12∂F∂x2x1∂F∂x1x2∂F∂x22∂F]=[2M+22M2M2M+2]
因为
M
>
0
M>0
M>0,所以
∇
2
F
\nabla^2F
∇2F为正定阵,即上述解为极小值。
看起来挺简单的,那是不是针对任意的约束优化问题,都可以通过构造罚函数,然后直接求梯度等于0,并让 M M M趋向无穷大后,得到最优解呢?
理论上好像可以,但实际上并不可行。主要原因有两点:
(1)很多优化问题的梯度计算特别复杂,甚至无法计算,比如使用各种智能优化算法求解的复杂问题;(2)即使可以推导出梯度公式,但是随着
M
M
M的增加,在边界处的梯度值越来越大,当
M
M
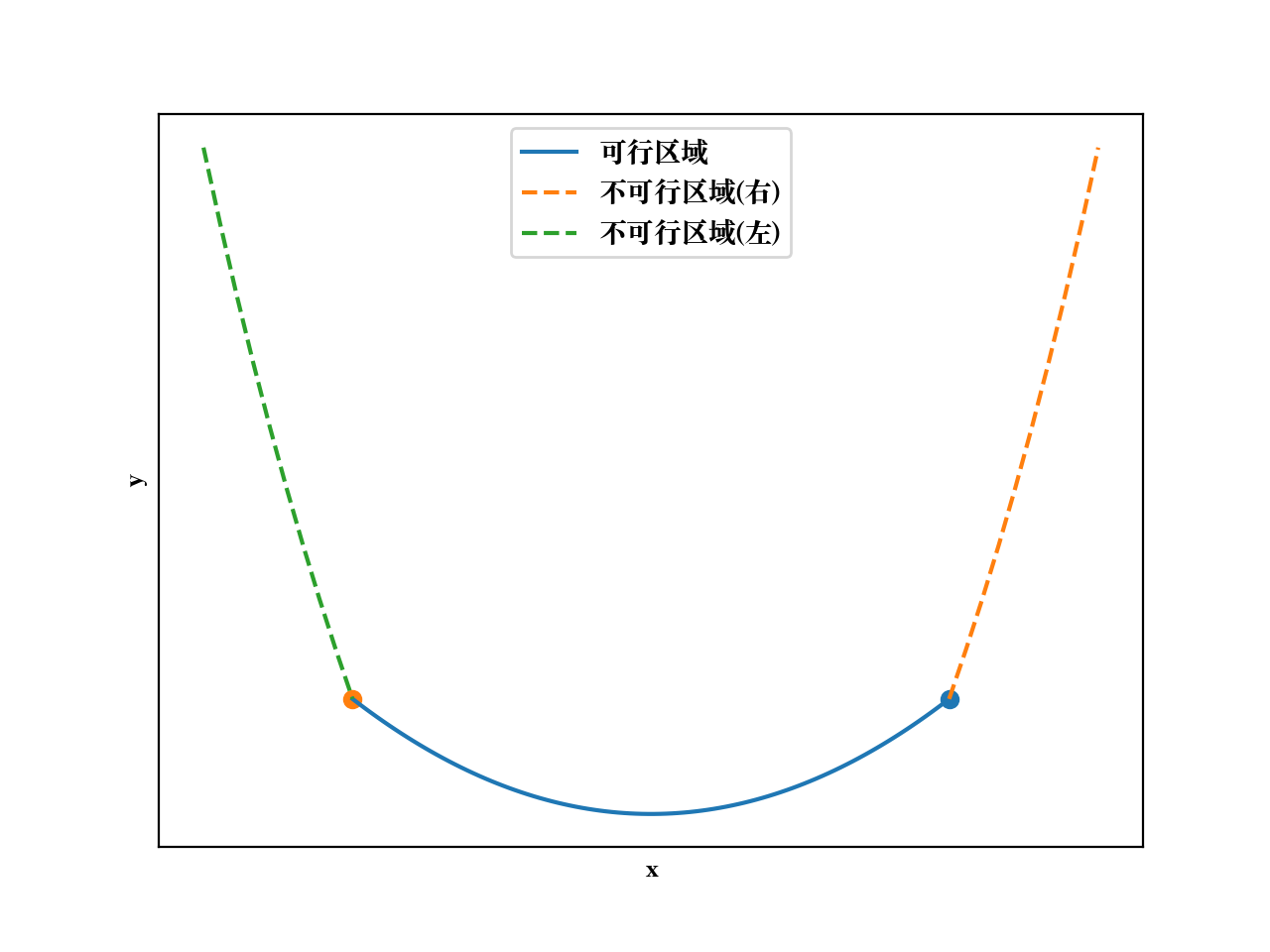
M已经极大时,可能会出现梯度爆炸的现象,而很多问题的最优解恰恰是在边界处取得,这就会给数值计算带来较大误差,下图中,由于加入了惩罚项,边界处(两个圆点)的左右值显然变化很大。
为了更好地使用使用罚函数法,一般的求解框架是这样设计的:
(1)给定初始点 x 0 \pmb x^0 x0,允许的惩罚项误差精度 ϵ \epsilon ϵ,初始 M 0 M_0 M0,以及每次 M M M的增长幅度 c ( c > 1 ) c(c>1) c(c>1)。
(2)以 x k − 1 \pmb x^{k-1} xk−1为初始点,求解无约束优化问题P1,得到最优解 x k \pmb x^k xk。
(3)如果 g ( x k ) ≤ ϵ g(\pmb x^k)≤\epsilon g(xk)≤ϵ,则停止迭代, x k \pmb x^k xk作为P的最优解;否则,令 M k + 1 = c M k M_{k+1}=cM_k Mk+1=cMk,转步骤2。
这里需要解释一下给定 x 0 \pmb x^0 x0的原因。求解P1时主要使用梯度类算法,所以是需要有个初值的,只不过此处初始点的选取是任意的,即可以在可行域外,也可以在可行域内;此外,求解 M k + 1 M_{k+1} Mk+1对应的P1时,需要使用 M k M_k Mk对应P1的最优解作为初值。
上述这种解决办法,在学术上还有一个更专业的称呼:外点罚函数法。
内点罚函数法
既然有外点罚函数法,那自然就还有内点罚函数法。
内点罚函数法的基本思想是在目标函数上引入一个关于约束的惩罚项,当迭代点由可行域的内部接近可行域的边界时, 惩罚项将趋于无穷大来迫使迭代点返回可行域的内部, 从而保持迭代点的严格可行性。
一种常见的新问题(P2)定义方式为:
min
F
(
x
,
R
)
=
f
(
x
)
−
R
⋅
∑
i
=
1
l
1
g
i
(
x
)
\text{min} \quad F(\pmb x,R)=f(\pmb x)-R·\sum_{i=1}^l\frac{1}{g_i(\pmb x)}
minF(x,R)=f(x)−R⋅i=1∑lgi(x)1
此处,
R
R
R为惩罚因子。
参考上一节的推理方式,我们可以得到如下结论:P2为P提供了上界,并且该上界在 R R R趋向于0时取到。
还是以上节的例子为例,目标函数变为
F
(
x
1
,
x
2
,
M
)
=
(
x
1
−
3
)
2
+
(
x
2
−
2
)
2
−
R
⋅
1
x
1
+
x
2
−
4
F(x_1,x_2,M)=(x_1-3)^2+(x_2-2)^2-R·\frac{1}{x_1+x_2-4}
F(x1,x2,M)=(x1−3)2+(x2−2)2−R⋅x1+x2−41
求梯度并令其等于0
∂
F
∂
x
1
=
2
(
x
1
−
3
)
+
R
⋅
1
(
x
1
+
x
2
−
4
)
2
=
0
\frac{\partial F}{\partial x_1}=2(x_1-3)+R·\frac{1}{(x_1+x_2-4)^2}=0
∂x1∂F=2(x1−3)+R⋅(x1+x2−4)21=0
∂
F
∂
x
2
=
2
(
x
2
−
2
)
+
R
⋅
1
(
x
1
+
x
2
−
4
)
2
=
0
\frac{\partial F}{\partial x_2}=2(x_2-2)+R·\frac{1}{(x_1+x_2-4)^2}=0
∂x2∂F=2(x2−2)+R⋅(x1+x2−4)21=0
上述两式相减,先得到变量间的对应关系
x
1
=
x
2
+
1
x_1=x_2+1
x1=x2+1
将该对应关系带入第二个梯度公式
(
x
2
−
2
)
(
2
x
2
−
3
)
2
=
−
R
2
(x_2-2)(2x_2-3)^2=-\frac{R}{2}
(x2−2)(2x2−3)2=−2R
R
→
0
R\rightarrow 0
R→0时,
x
2
x_2
x2存在两个可行解:2和3/2。
回到刚刚的对应关系,可以得到 x 1 = 3 x_1=3 x1=3和 x 1 = 5 / 2 x_1=5/2 x1=5/2。
显然,只有第二组解符合约束条件 x 1 + x 2 − 4 ≤ 0 x_1+x_2-4≤0 x1+x2−4≤0。而该解和外点罚函数法的解是完全一致的。
需要说明的是,相比外点罚函数法,内点罚函数法要求可行解始终保持在可行域内,并且不能直接处理含等式约束的最优化问题。受限于这些条件,内点罚函数法在实际问题中的通用性不如外点罚函数法。
罚函数法 vs 拉格朗日乘子法
既然罚函数法和拉格朗日乘子法都是解决约束优化问题的方法,那么就有必要放在一起横向对比一下。
浏览了一些网上关于这两种方法的对比,很多是从对偶角度入手的,不过暂时我还不太懂对偶,所以打算从算法设计的思路来阐述。
罚函数法的思路,有种逐步逼近最优解的状态:持续增加惩罚因子值后,新构造的无约束优化问题的最优解便会越来越逼近原约束优化问题的上界(内惩罚)或下界(外惩罚);在此过程中,惩罚因子是以参数形式被引入的,所以原问题未扩维。
拉格朗日乘子法的思路,则更像是一步到位的策略:直接证明了新构造的无约束优化问题的最优解等价于原约束优化问题的最优解;在此过程中,拉格朗日乘子则是以优化变量的身份被引入的,所以原问题相当于被升维到更高空间去解决。