场景：就是A项目的组件需要在B项目中使用

下面举例的是把a项目pagination分页组件上传到npm，在b项目使用

采坑日记：封装的组件一定要起name要不调用不成功

1.1 配置打包

1.1 首先在公用组件components文件夹下创建index.js文件，

 1.2 index.js

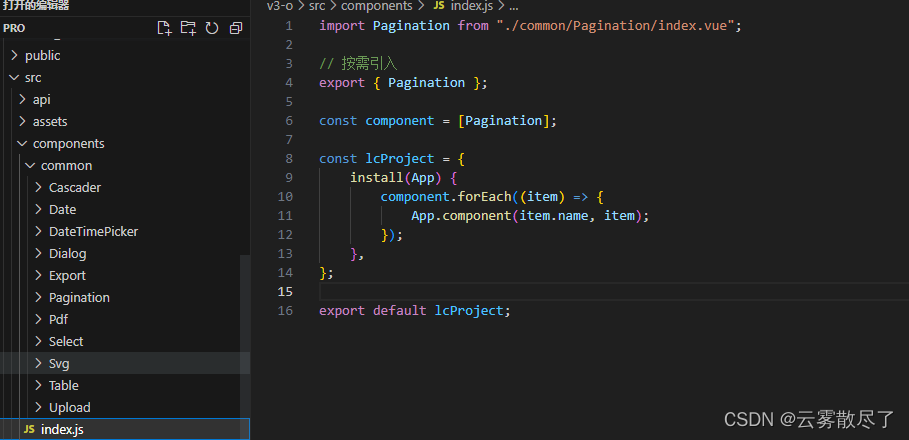
 1.3 vite.config.js

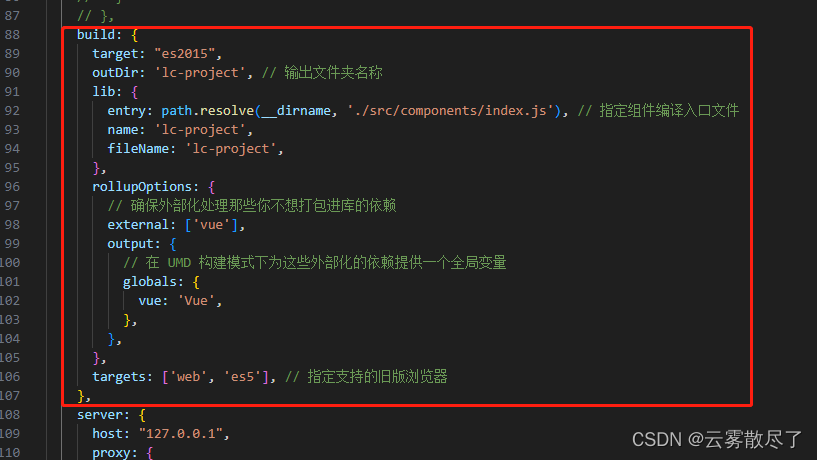
 1.4 package.json

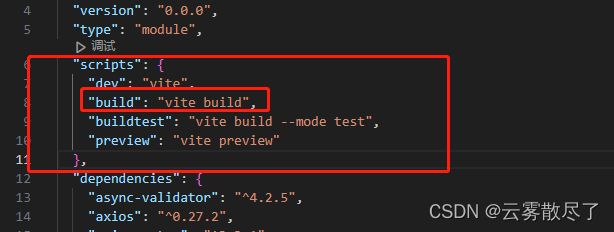
 执行npm run build打包，出现如图文件夹则代表打包成功

 2.1 上传npm官网

2.1 cd lc-project 执行npm init -y，我的配置如下图

name：上传后的名称

description：版本描述

version：版本号

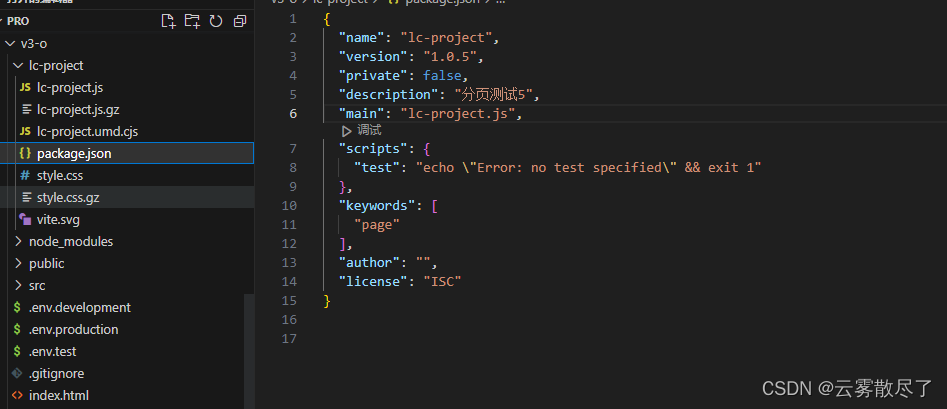
 2.2 上传到npm，首先得注册个npm账号 官网 记住用户名、密码和邮箱，发布的时候会用到

 2.3 设置npm源，一般都是淘宝镜像，需要切换官方镜像

npm config set registry=https://registry.npmjs.org

 2.4 文件根目录打开终端，输入npm login

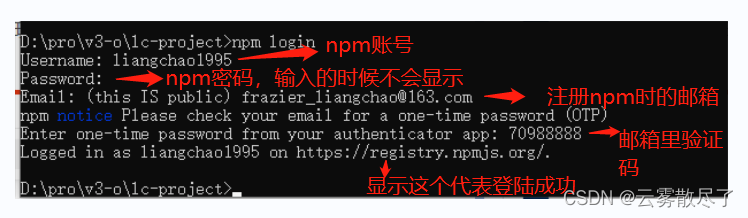
   2.5 在v3-o\lc-project目录下执行 npm publish 命令，出现  + lc-project@1.0.1 则代表上传成功，可以官网查看下

 3.1 B项目中应用

  3.1 打开终端执行npm i lc-project

  3.2然后在main.js中

import "../node_modules/lc-project/style.css"; //引入组件样式
import lcProject from "lc-project"; //引入下载后的组件
app.use(lcProject);
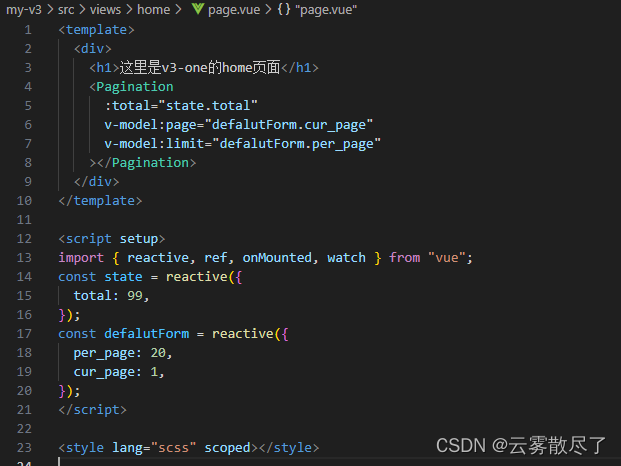
app.mount("#app");

  3.3 在B项目组件中直接使用就行