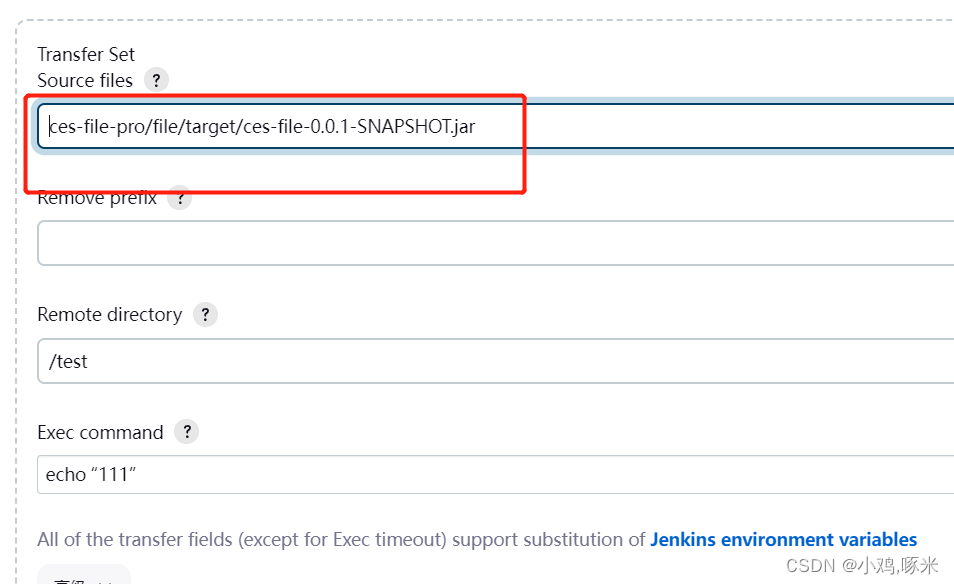
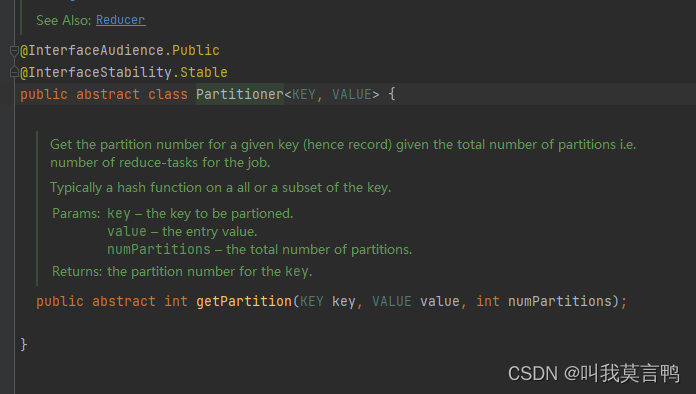
思路1：
0.输入一个值作为n
1.假设输入的n==4计算4^3=64.
2.因为他们都是连续的奇数可以把它写成另一种方法，每一个数之间相差2。
4^3=13+(13+2)+(13+4)+(13+6);
3.64-(2+4+6)=52–>52/4等于13
4.这样的话我们就找到了连续奇数的第一个数字。

//具体代码：
#include <stdio.h>
#include<math.h>
int main()
{
    //输入：
    int n = 0;
    scanf("%d", &n);
    //计算次方的数值
    int sum = 0;
    sum = (int)pow(n, 3);
    //找这些数字
    //1.每次增加2，计算总共的和。
    int sum_1 = 0;
    int i = 2;
    int k = n;
    while (k>1)
    {
        sum_1 += i;
        k--;
        i += 2;
    }
    //计算初始的数值
    int b = 0;
    int init = ((sum - sum_1) / n);
    for (i = 1, b = 0; i <= n; i++, b += 2)
    {
        if (i <= n - 1)
        {
            printf("%d+", init+b);
        }
        else if (i == n)
        {
            printf("%d", init+b);
        }
    }
    return 0;
}

思路2：
//1.当n是奇数n^2存在这个连续的奇数中并且是中间的数值。
//2.当n是偶数n^2不存在这个连续的奇数中但是，这个数值是最中间的数值。
//比如说4^2==16; 13+15(16-1) + (16+1)17+19
//3.定义一个数组去从中间向两边去赋值。

#include<stdio.h>

int main()
{
	int n = 0;
	scanf("%d", &n);

	int middle = 0;
	middle = n * n;
	int num[100] = {0};

	//偶数
	if (n % 2 == 0)
	{
		int k_l = (n / 2)-1;
		int k_r = n / 2;
		int i = 0;
		for (i = 0; i < n / 2; i++)
		{
			if (i == 0)
			{
				num[k_l] = middle - 1;
				num[k_r] = middle + 1;
				k_l -= 1;
				k_r += 1;
			}
			else
			{
				num[k_l] = num[k_l + 1] - 2;
				num[k_r] = num[k_r - 1] + 2;
				k_l -= 1;
				k_r += 1;
			}
		}

	}


	//奇数
	if (n % 2 == 1)
	{
		int k_l = (n / 2) - 1;
		int k_r = (n / 2) + 1;
		int i = 0;
		for (i = 0; i < (n / 2) + 1; i++)
		{
			if (i == 0)
			{
				num[n / 2] = middle;
			}
			else
			{
				num[k_l] = num[k_l + 1] - 2;
				num[k_r] = num[k_r - 1] + 2;
				k_l -= 1;
				k_r += 1;
			}
		}

	}

	for (int i = 0; i < n; i++)
	{
		if (i == n - 1)
		{
			printf("%d", num[i]);
		}
		else
		{
			printf("%d+", num[i]);
		}
	}
	return 0;
}