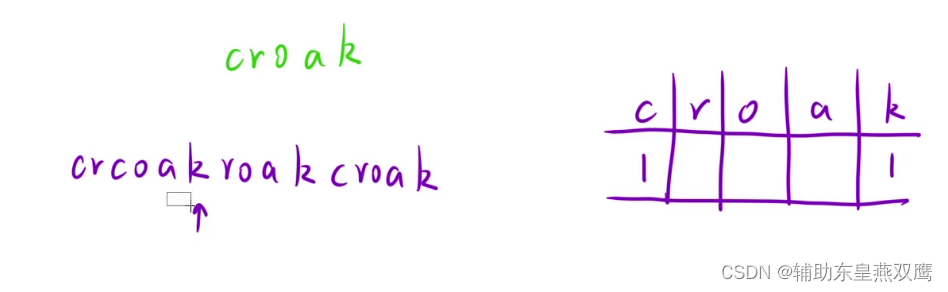1)替换所有的问号:
1)模拟算法流程,一定要在草稿纸上过一遍流程
2)将流程转化成代码
1576. 替换所有的问号 - 力扣(Leetcode)
class Solution { public String modifyString(String s) { char[] array=s.toCharArray(); for(int i=0;i<array.length;i++){ if(array[i]=='?'){ for(char ch='a';ch<='z';ch++){ //1.当i==0的时候其实是处于最前面的位置,前面这个字符不存在直接就判断后面这个字符即可 //或者是前面这个字符是存在的,和前面的字符不相等即可 //2.就是当i==0或者是i==array.length-1的情况是不需要进行判断 if((i==0||ch!=array[i-1])&&(i==array.length-1||ch!=array[i+1])){ array[i]=ch; break; }else{ continue; } } } } //将字符数组转化成字符串 return String.valueOf(array); } }2)提莫攻击:
495. 提莫攻击 - 力扣(Leetcode)
class Solution { public int findPoisonedDuration(int[] timeSeries, int duration) { int time=0; for(int i=1;i<timeSeries.length;i++){ int end=timeSeries[i]; int start=timeSeries[i-1]; if(end-start<=duration) time+=end-start; else time+=duration; } return time+duration; } }算法原理:
1)先进行计算两次受到攻击的时候,所受到攻击时间的差值,如果差值是大于等于duaration的话,大于中毒时间,说明在前面所收到的攻击总的中毒时间是需要进行全部累加上的,因为两次受到的攻击时间是有差值的,当这段差值是大于等于中毒时间的,说明你在a点受到攻击之后,在受到下一次攻击之前,这个中毒时间已经全部承受了,所以中毒时间需要全部进行累加
2)再进行计算两次攻击的时候,所受到的攻击时间的差值是小于duartion,相当于是你在受到第一次攻击之后,这一次的中毒时间还没有完全过去,就又来了一次攻击,中毒时间又被重置,那么两次受到攻击的这段时间的差值就是a-b,此时所进行计算的中毒时间是不包含第二次攻击所包含的那一秒的
3)当受到最后一次攻击的时候,那么最后这一次中毒时间是一定可以持续完的
3)N字形变换:
6. N 字形变换 - 力扣(LeetCode)
解法1:暴力破解
将所有字符存放到一个二维数组
class Solution { public String convert(String s, int numRows) { if(numRows==1) return s; char[][] dp=new char[numRows][s.length()]; char[] array=s.toCharArray(); int col=0; int row=0; int index=0; StringBuilder result=new StringBuilder(); while(index<array.length){ while(index<array.length&&row<numRows){ dp[row][col]=array[index]; row++; index++; } col++; row=row-2; while(index<array.length&&row>=0&&col<array.length){ dp[row][col]=array[index]; col++; row--; index++; } row+=2; col--; } for(int i=0;i<numRows;i++){ for(int j=0;j<s.length();j++){ if(dp[i][j]!='\u0000') result.append(dp[i][j]); } } return result.toString(); } }解法2:根据分组周期性拼接:
class Solution { public String convert(String s, int numRows) { if(numRows==1) return s; char[] array=s.toCharArray(); int period=2*numRows-2; //1.创建一个字符串数组用来存放每一行字符拼接的结果 String[] strings=new String[numRows];//默认的初始化结果都是null,必须给字符串数组全部初始化成"" for(int i=0;i<strings.length;i++){ strings[i]=""; } //2.进行计算每一个字符应该存放在字符串数组中的每一行 for(int i=0;i<array.length;i++){ int mod=i%period; if(mod<numRows){ strings[mod]+=array[i]; }else{ strings[period-mod]+=array[i]; } } //3.遍历字符数组返回结果 StringBuilder sb=new StringBuilder(); for(String str:strings){ System.out.println(str); sb.append(str); } return sb.toString(); } }解法三:找规律
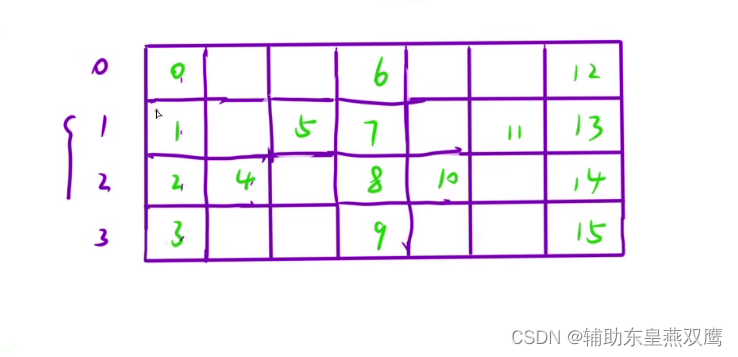
把原始的模拟结果给画出来,再找规律,推导出规律之后说明这个规律是正确的
String str="abcdefghijk"
我们将字符串转化成数组,将下标填写到N自行变换的对应位置
1)首先我们先找第一行和最后一行的元素下标的对应关系
首先进行观察,第一行第一个元素和第二个元素之间以及第二个元素到第一行第三个元素之间都相差了2N-2个元素(N是行数)
所以第一行的字符就是:0 0+2N-2 0+1*(2N-2) 0+K(2N-2)
所以说最后一行的元素的组合就是:N-1,N-1+(2N-2),N-1+2*(2N-2),N-1+K(2N-2)
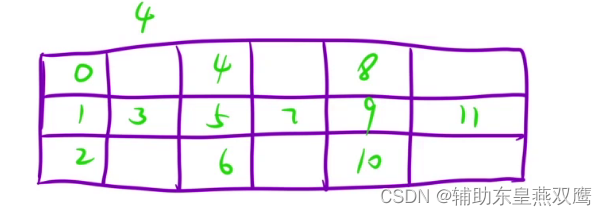
2)现在来寻找一下除了第一行和最后一行的元素的规律:已知公差是D=2N-2
别的行前两个元素是K和D-K
后面的元素依次是K+D,D-K+D,两个偶数对依次向后+D
这个规律针对于所有的K都适用
class Solution { public String convert(String s, int numRows) { if(numRows==1) return s; char[] array=s.toCharArray(); StringBuilder sb=new StringBuilder(); String[] strings=new String[numRows]; int index=0; for(int i=0;i<numRows;i++){ strings[i]=""; } int period=2*numRows-2; //1.先进行处理第一行 while(index<array.length){ strings[0]+=array[index]; index=index+period; } //2.在来进行处理最后一行 index=numRows-1; while(index<array.length){ strings[numRows-1]+=array[index]; index=index+period; } //3.处理中间两行 for(int i=1;i<=numRows-2;i++){ int start=i; int end=period-i; while(start<array.length||end<array.length){ //注意这里面不可以写成&&因为end越界了但是start可能没有越界 if(start<array.length)strings[i]+=array[start]; if(end<array.length)strings[i]+=array[end]; start=start+period; end=end+period; } } //4.返回结果 for(int i=0;i<strings.length;i++){ sb.append(strings[i]); } return sb.toString(); } }4)外观数列:
算法原理:如何找到对上一个数的解释+双指针
38. 外观数列 - 力扣(LeetCode)
class Solution { public String countAndSay(int n) { if(n==1) return "1"; String s="1"; StringBuilder sb=null; for(int i=1;i<n;i++){ int left=0; int right=0; sb=new StringBuilder(); char[] array=s.toCharArray(); while(right<s.length()){ while(right<array.length&&array[right]==array[left]){ right++; } sb.append(right-left); sb.append(array[left]); left=right; } s=sb.toString(); System.out.println(s); } return sb.toString(); } }
4)数青蛙
模拟+哈希表
1419. 数青蛙 - 力扣(LeetCode)
算法原理:
1)完美模拟的情况:正好能够叫出一个青蛙该叫出来的所有字符的情况
1)当字符串从前向后进行遍历的时候,当遍历到r字符的时候,只需要看看前面有没有c字符即可,有没有青蛙叫出c字符即可,所以我们每当遍历到一个字符的时候,还需要进行统计前一个字符出现的情况
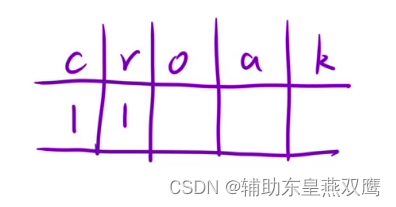
2)就拿这个字符串举例来说,当进行遍历到c字符的时候,有一个青蛙开始叫了,字符c对应的value就置为1,当遍历到r的时候,看看前面有没有c字符出现过,发现有c字符出现过,那么于是就让c字符出现的次数--,r出现的次数++
3)当进行遍历到o的时候,于是去前面找找有没有一个青蛙叫出r这个字符,发现有,那么就让r--,o++
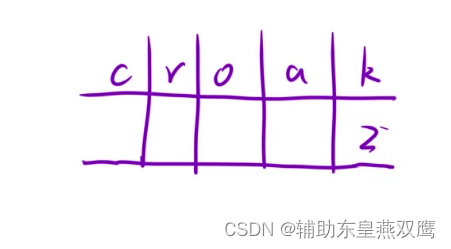
4)以此类推,直到遍历整个字符串,当我们发现K的值等于2的时候,此时发现遍历字符串的位置又从c开始了,因为我们求的是最少的青蛙的个数,于是我们可以让k--,c=1,剥离出一个青蛙从头开始叫
最终K存放的值就是最终结果,况且CROA的哈希表中存放的个数都是0,想象一下,如果CROK中的字符有一个不等于0,那么说明这个青蛙还没有叫完字符串的遍历就终止了
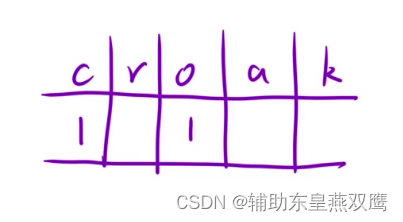
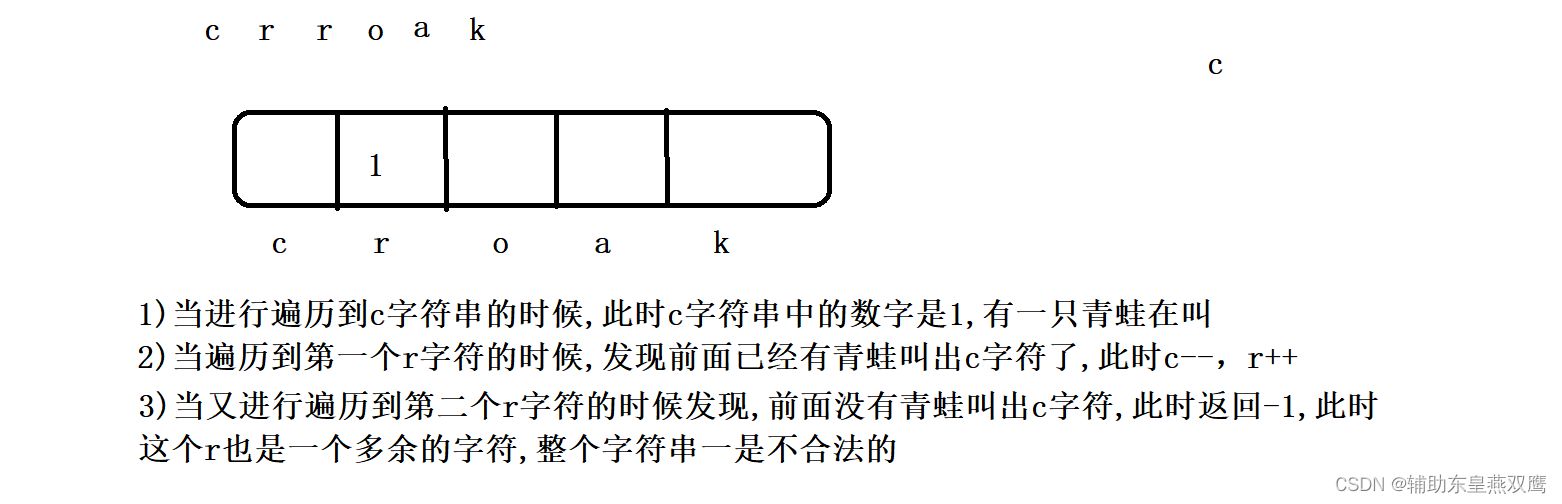
2)模拟失败的情况:
假设现在字符是crroak
也就是是说每当我们进行遍历到一个字符的时候,都是需要进行检查前面的字符有没有出现过,没有出现过就直接返回-1,如果出现过就让前面的字符--,当前字符++
3)总结:
1)当进行遍历到r o a k的时候,找一下前驱字符,看看是否在哈希表中出现过,如果存在,那么前驱字符减减,当前字符++,如果这个字符的前驱字符不存在,那么直接返回-1,说明前面的字符没有青蛙叫过,此时说明这个字符非法,这个字符串也是非法的;
2)当遍历到c字符的时候,看看这个最后一个字符是否在哈希表中存在过,如果最后一个字符存在的话,说明已经有青蛙叫完了,那就尝试从头开始叫,那就让最后一个字符--,当前c字符++,如果最后一个字符没有出现过,那么说明没有一个青蛙叫到最后一个字符,此时说明是第一个青蛙叫到c字符,此时c++即可
3)当遍历完所有字符的时候,看看k前面的字符出现次数是否是0,如果不是0,说明有青蛙没叫完,就直接返回-1,字符串非法
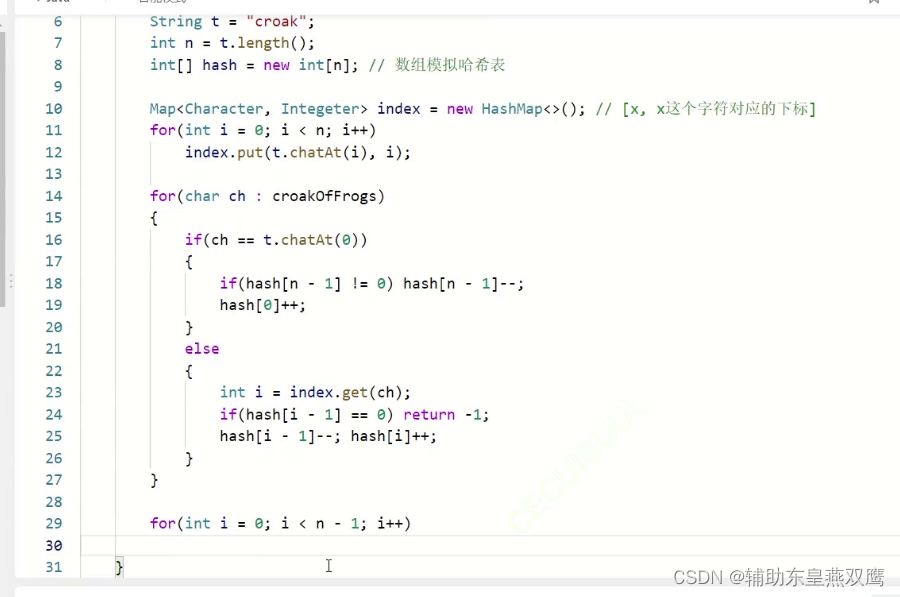
class Solution { public int minNumberOfFrogs(String str) { char[] array=str.toCharArray(); int[] CountArray=new int[200]; String s="croak"; for(int i=0;i<str.length();i++){ if(array[i]=='r'||array[i]=='o'||array[i]=='a'||array[i]=='k'){ int index=s.indexOf(array[i]); System.out.println(index); if(CountArray[s.charAt(index-1)]==0){ //这里面不是CountArray[i-1] return -1; }else{ CountArray[array[i]]++; CountArray[s.charAt(index-1)]--; } }else{ if(CountArray['k']>0){ CountArray['c']++; CountArray['k']--; }else{ CountArray['c']++; } } } for(int i=0;i<array.length;i++){ if(array[i]=='r'||array[i]=='o'||array[i]=='a'||array[i]=='c'){ if(CountArray[array[i]]>0){ return -1; } } } return CountArray['k']; } }class Solution { public int minNumberOfFrogs(String str) { char[] array=str.toCharArray(); int[] CountArray=new int[200]; String s="croak"; for(int i=0;i<str.length();i++){ if(array[i]!=s.charAt(0)){ int index=s.indexOf(array[i]); System.out.println(index); if(CountArray[s.charAt(index-1)]==0){ return -1; }else{ CountArray[array[i]]++; CountArray[s.charAt(index-1)]--; } }else{ if(CountArray[s.charAt(s.length()-1)]>0){ CountArray[array[i]]++; CountArray[s.charAt(s.length()-1)]--; }else{ CountArray[array[i]]++; } } } for(int i=0;i<array.length;i++){ if(array[i]!=s.charAt(s.length()-1)){ if(CountArray[array[i]]>0){ return -1; } } } return CountArray[s.charAt(s.length()-1)]; } }写法三: