博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译：https://yalmip.github.io/tutorials/

之前的博客简单介绍了约束条件的定义方法，接下来将对其进行详细介绍。

首先简单复习一下：

1.定义约束条件可以使用矩阵拼接，或者’+’号，两种方式是等价的；

2.Yalmip中的约束可以写成连续的不等式形式；

3.Yalmip中不支持严格的不等号(<或>)，一旦出现，就会报错，然后弹出“猫猫图”。

下面将继续讲解约束条件定义的方法与技巧。

1.约束的普通形式与矩阵形式

例1：请使用Yalmip工具箱写出下列优化问题的约束条件

采用常规的思维，可以分别写出每个约束条件，然后采用拼接的方式将所有约束条件组合起来，matlab代码如下：

x = sdpvar(3,1);

C = [sum(x) <= 12 ,...

     5*x(1) + x(3) <= 9 ,...

     3*x(1) + 2*x(2) >= 6 ,...

     x(2) + 2*x(3) >= 1 ,...

     x >= 0];

但是在求解优化问题的过程中，很多时候需要我们写出优化问题的对偶形式或KKT条件，这时候如果可以写成紧凑的矩阵形式，转换将会更加容易。例1的约束条件写成紧凑的矩阵形式为：

将约束条件写作矩阵形式时，代码如下：

x = sdpvar(3,1);
A = [-1   0   0;
      0  -1   0;
      0   0  -1;
      1   1   1;
      5   0   1;
     -3  -2   0;
      0  -1  -2];
b = [0;0;0;12;9;-6;-1];
C = [A*x <= b];

两种写法是完全等价的，下面的代码分别采用两种不同的约束定义方式对优化问题进行求解，可以得到相同的优化结果：

clc
clear
 
x = sdpvar(3,1);
A = [-1   0   0;
      0  -1   0;
      0   0  -1;
      1   1   1;
      5   0   1;
     -3  -2   0;
      0  -1  -2];
b = [0;0;0;12;9;-6;-1];
C1 = [A*x <= b];
C2 = [sum(x) <= 12 ,...
      5*x(1) + x(3) <= 9 ,...
      3*x(1) + 2*x(2) >= 6 ,...
      x(2) + 2*x(3) >= 1 ,...
      x >= 0];
objective = [1 2 3]*x;
optimize(C1 , objective);
objective1 = value(objective)
x1 = value(x)
optimize(C2 , objective);
objective2 = value(objective)
x2 = value(x)

运行结果：

objective1 =

    3.3333


x1 =

    1.3333
    1.0000
         0

objective2 =

    3.3333


x2 =

    1.3333
    1.0000
         0

在实际编程过程中，两种形式各有优劣，但完全等价，可以根据自己的需要采用一般形式或矩阵形式定义约束条件，只要自己感觉更方便即可。

2.小技巧

2.1查看约束变量的参数

在定义约束条件之后，在工作区双击对应的约束变量，或者在命令行输入约束变量再回车，可以查看约束的列表，并检查约束是否已有效定义了，例如，例1中用两种不同方式定义的约束条件列表分别如下：

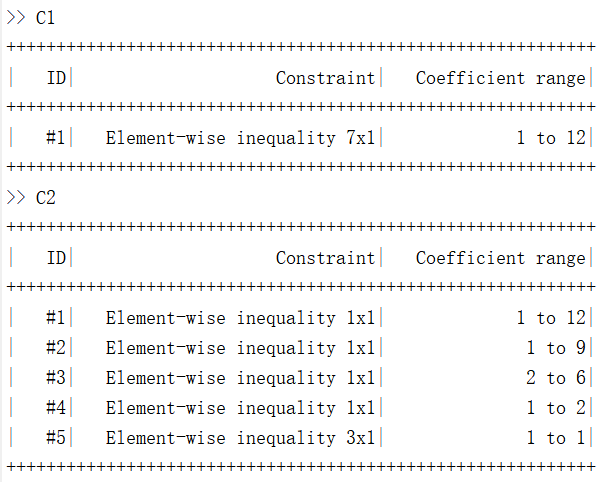
在该列表中，ID一列表示约束的编号，每个约束都是用’，’或者’+’隔开的，因此约束变量C1中仅有1个约束，约束变量C2中共有5条约束。Constraint一列表示约束的类型和数目，Element-wise inequality表示该约束条件为不等式约束，如果是等式约束，则显示‘Equality constraint’，其他一些常见的约束类型如表1所示。约束类型后面显示的是约束的数目，例如约束变量C1共包含七条约束，因此显示为7×1的约束，而约束变量C2中的第五条约束x>=0，实际上包含x1>=0,x2>=0,x3>=0共三条约束，因此显示为3×1的约束。

表1 常见的约束类型

约束类型	含义
Matrix inequality	矩阵不等式约束
Second order cone constraint	二阶锥约束
Rotated Lorentz constraint	旋转锥约束
Binary constraint	二进制约束
Eigenvalue constraint	特征值约束
KYP constraint	Kalman Yakubovich Popov 约束
Sum-of-square constraint	平方和约束
Logic constraint	逻辑约束
Semi-continuous variable	半连续的变量约束
Semi-integer variable	半整数的变量约束
Vectorized second-order cone constraints	矢量化二阶锥约束

2.2尽量避免使用循环语句

在Yalmip工具箱中，大部分matlab内置函数都可以用于sdpvar变量。之前我写过几篇博客说明如何在matlab代码中尽量避免循环的使用，以提升代码运行效率，因此也可将这种思想用于约束条件的定义过程中。下面以Yalmip工具箱官方文档中给出的数独求解的算例（https://yalmip.github.io/example/sudoku/）进行说明。

例2：使用Yalmip工具箱求解图1所示的数独问题

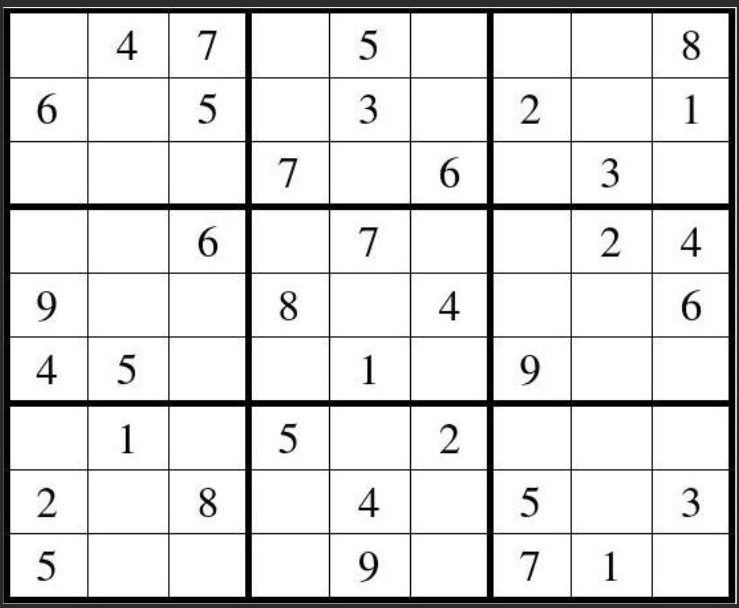
图1 一个数独问题

为了求解这个问题，可以定义一个9×9×9的三维0-1变量A(i,j,k)，当A(i,j,k)取值为1时，表示该数独的第i行第k列的取值为k，为了求解上述数独问题，需要写成初始的数独矩阵，并定义决策变量A：

A0 = [
0 4 7 0 5 0 0 0 8;
6 0 5 0 3 0 2 0 1;
0 0 0 7 0 6 0 3 0;
0 0 6 0 7 0 0 2 4;
9 0 0 8 0 4 0 0 6;
4 5 0 0 1 0 9 0 0;
0 1 0 5 0 2 0 0 0;
2 0 8 0 4 0 5 0 3;
5 0 0 0 9 0 7 1 0;
];
 
A = binvar(9,9,9,'full');

首先，我们需要把变量A中的元素取值和初始矩阵A0对应起来，代码如下：

for i = 1:9
    for j = 1:9
        if S(i,j)
            F = [F, A(i,j,A0(i,j)) == 1];
        end
    end
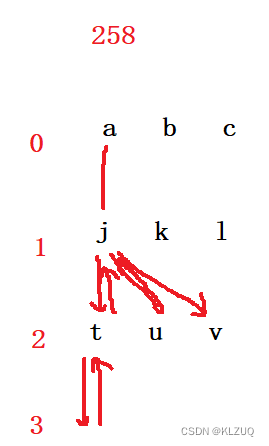
end

这也是常规使用循环语句的思维，但是，如果使用find和sub2ind命令，可以避免循环语句的使用。find函数比较常用，也比较简单，这里不再介绍，重点介绍一下sub2ind。该函数用于将下标向量组转为线性索引，具体的含义我们可以通过一个例子来理解。假设在matlab中有一个矩阵3×3的矩阵S，我们如果想取出矩阵S第3行第2列的元素，可以采用下标的形式写成S(3,2)，如果采用线性索引的话，也可以写成A(6)。下标和线性索引的关系如图2所示：

图2 matlab二维数组中下标和线性索引的关系

sub2ind就可以把一组下标转为一组线性索引，以避免循环的使用，标准语法为：

ind = sub2ind(sz,row,col)

例如，我们要取出矩阵S的元素S(1,2)，S(1,3)，S(2,2)和S(3,2)，也就是要求出线性索引向量[4 5 6 7]，采用sub2ind函数即可解决：

row = [1 2 3 1];
col = [2 2 2 3];
sz = [3 3];
ind = sub2ind(sz,row,col)

输出结果为：

ind =

     4     5     6     7

因此，使用find与sub2ind，可以将上述代码改写成：

[i,j,k] = find(A0);
F = [F, A(sub2ind(size(A),i,j,k)) == 1];

这样做就可以避免使用双层循环。另外，数独游戏的规则是，每一行、每一列以及每一个3×3的子块的数字不能重复，其中每行每列数字不能重复的约束比较简单，代码如下：

F = [sum(A,1) == 1, sum(A,2) == 1, sum(A,3) == 1];

要保证每个3×3的子块数字不能重复，可以采用循环的方式，代码如下：

for m = 1:3
    for n = 1:3
        for k = 1:9
            s = sum(sum(A((m-1)*3+(1:3),(n-1)*3+(1:3),k)));             
            F = [F, s == 1];
        end
    end
end

为了尽量避免使用循环语句，可以将代码改写如下：

for k = 1:9
    F = [F, sum(sum(A(i1:i1+2 , j1:j1+2 , :))) == 1];
end

这样写可以只用一层循环，具体原理比较简单，这里不再过多讲解。另外，对于数独问题，我们只需要求出可行解，并没有优化目标，因此使用optimize函数时可以只输入约束条件。

sol = optimize(F);

求解成功后，可以使用一个矩阵Z来存储最终的数独求解结果：

Z = 0;
for i = 1:9
      Z = Z  + i*value(A(:,:,i));
end
Z

为了避免循环语句，也可以写成：

Z = value(reshape(A,9,81)*kron((1:9)',eye(9)))

其中，reshape函数用于改变矩阵的形状，并返回一个新的矩阵。在这条语句中，reshape(A,9,81)表示将矩阵A重塑为一个9行81列的矩阵。kron函数用于计算两个矩阵的张量积，在这条语句中，kron((1:9)',eye(9))可以得到一个81行9列的矩阵，其中对应位置的元素由(1:9)'和单位矩阵的元素相乘得到。将矩阵reshape(A,9,81)与矩阵kron((1:9)',eye(9))，得到的就是9×9的矩阵，也就是数独问题的解。

综上所示，使用常规思维+更多的循环语句求解数独问题的完整代码如下：

方法1：放肆使用循环语句

clc
clear
 
tic
A0 = [
0 4 7 0 5 0 0 0 8;
6 0 5 0 3 0 2 0 1;
0 0 0 7 0 6 0 3 0;
0 0 6 0 7 0 0 2 4;
9 0 0 8 0 4 0 0 6;
4 5 0 0 1 0 9 0 0;
0 1 0 5 0 2 0 0 0;
2 0 8 0 4 0 5 0 3;
5 0 0 0 9 0 7 1 0;
];
 
A = binvar(9,9,9,'full');
F = [sum(A,1) == 1, sum(A,2) == 1, sum(A,3) == 1];
 
for i = 1:9
    for j = 1:9
        if A0(i,j)
            F = [F, A(i,j,A0(i,j)) == 1];
        end
    end
end
 
for m = 1:3
    for n = 1:3
        for k = 1:9
            s = sum(sum(A((m-1)*3+(1:3),(n-1)*3+(1:3),k)));             
            F = [F, s == 1];
        end
    end
end
 
diagnostics = optimize(F);
 
Z = 0;
for i = 1:9
      Z = Z  + i*value(A(:,:,i));
end
Z
toc

方法2：尽量减少循环语句

clc
clear

tic
A0 = [
5 3 0 0 7 0 0 0 0;
6 0 0 1 9 5 0 0 0;
0 9 8 0 0 0 0 6 0;
8 0 0 0 6 0 0 0 3;
4 0 0 8 0 3 0 0 1;
7 0 0 0 2 0 0 0 6;
0 6 0 0 0 0 2 8 0;
0 0 0 4 1 9 0 0 5;
0 0 0 0 8 0 0 7 9;
];

A = binvar(9,9,9,'full');

F = [sum(A,1) == 1, sum(A,2) == 1, sum(A,3) == 1];

i1 = [1,1,1,4,4,4,7,7,7];
j1 = [1,4,7,1,4,7,1,4,7];
for k = 1:9
    F = [F, sum(sum(A(i1:i1+2 , j1:j1+2 , :))) == 1];
end

[i,j,k] = find(A0);
F = [F, A(sub2ind(size(A),i,j,k)) == 1];

diagnostics = optimize(F);

Z = value(reshape(A,9,81)*kron((1:9)',eye(9)))
toc

两种方式的运行结果完全一致：

Z =

     3     4     7     2     5     1     6     9     8
     6     8     5     4     3     9     2     7     1
     1     2     9     7     8     6     4     3     5
     8     3     6     9     7     5     1     2     4
     9     7     1     8     2     4     3     5     6
     4     5     2     6     1     3     9     8     7
     7     1     3     5     6     2     8     4     9
     2     9     8     1     4     7     5     6     3
     5     6     4     3     9     8     7     1     2

但在运行时间上，两种方法存在差异，某次测试中，方法1的运行时间为0.638127秒，方法2的运行时间为0.473180秒，避免循环的使用提高了25.85%的运行效率。

减少循环语句的使用，在小规模问题中效率提升可能不是很明显，但如果优化问题比较复杂，约束也很复杂，如果可以把尽量减少循环语句的思想应用到实际编程中，效率提升可能是非常大的。虽然思考如何减少循环语句可能要废很多脑细胞，但我觉得应该会挺值得。(我自己经历过一个优化问题求解需要8个小时左右，每次等待结果、调试代码都非常痛苦，将近半个月都没有调好，后来想通了，花了两三天的时间优化代码，把运行时间缩短到了1个半小时左右，很快就调试成功了)

3.测试题

3.1测试1

使用矩阵形式的约束条件求解下列优化问题：

max z=3x1+x2

s.t. x1-x2≥-2

x1-2x2≤3

3x1+2x2≤14

x1≥0, x2≥0

3.2测试2

使用Yalmip工具箱求下列数独问题的解：

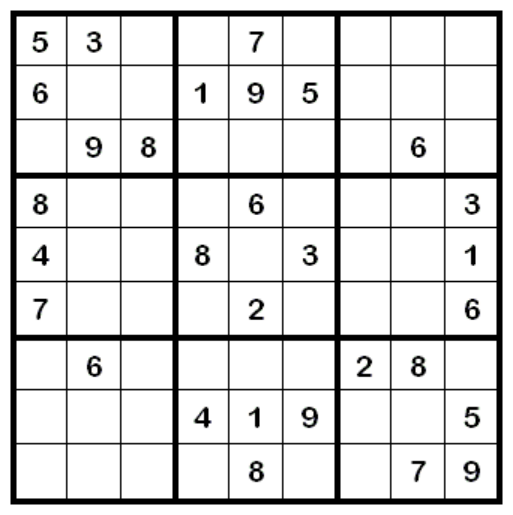
3.3测试3

改写下面的代码以避免使用循环语句，并对比两种方式的代码运行时间。

clc
clear
yalmip('clear')
 
tic
n = 50;
a = rand(n,n,n);
x = sdpvar(n,n,n);
z = 0;
for k = 1:n
    for kk = 1:n
        for kkk = 1:n
            z = z + a(k,kk,kkk) * x(k,kk,kkk);
        end
    end
end
toc