AI for Science日益表现出突破传统科学研究能力瓶颈的巨大潜力，正在成为全球科学研究新范式。近年来，各学科不断加入，模型精度、泛化性逐渐提高，不同技术路径、不同应用场景的AI for Science成功应用不断涌现，深度融合领域知识的AI for Science基础软件也蓬勃发展，为各领域AI for Science研究人员提供了一大批简单易用的工具软件。

百度飞桨作为拥有国内最大开源用户群体的深度学习平台，一直致力于将AI方法应用于基础科研，通过不断提升飞桨框架对科学问题的求解机制，并建设端到端的科学计算工具组件来加速AI与传统科学研究的融合。在过去的一年中，飞桨框架通过全量支持开源科学计算工具DeepXDE以及对大量科学领域论文代码的重构，进一步完善了飞桨科学计算的机制，并形成了赛桨PaddleScience v1.0的四大特色能力：

从易用性角度，兼顾用户体验，进行了API架构的更新；
支持更广泛的底层模型，如CNN、U-Net、Transformer等；
提供丰富的场景案例，如2D&3D圆柱绕流、涡激振动等基础案例以及气象预报、污染物扩散等行业案例；
更加全面的API支持，如自定义偏微分方程及各类边界条件、支持2D&3D基础几何定义等。

飞桨AI for Science功能全景如下图所示。

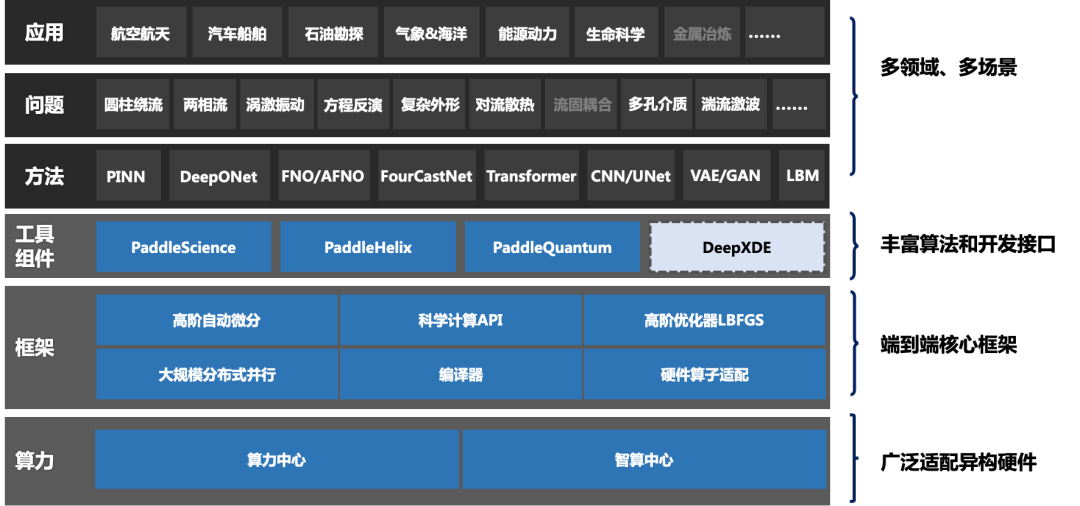
图飞桨AI4S全景图

飞桨框架的技术创新

为了有力支撑科学计算高阶微分方程求解等任务需求，飞桨框架对整体训练架构进行升级，在不改变现有用户使用习惯的基础上，用户可以使用飞桨框架API进行动态图组网调试，并通过动转静、算子组合、编译优化技术提升训练性能。

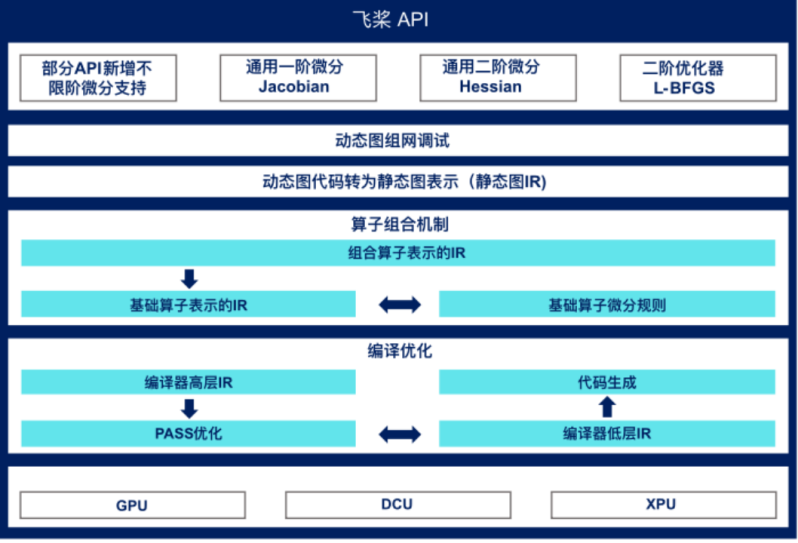
图框架技术创新

飞桨框架 API

基于上述训练架构，飞桨可以低成本方式支持高阶自动微分，不再需要通过手写高阶微分算子，当前飞桨框架支持50多个常用API高阶自动微分，并可持续扩展，已在EulerBeam、圆柱绕流等40+案例及模型验证。除此之外，飞桨支持科学计算所需的通用一阶微分Jacobian、通用二阶微分Hessian、二阶优化器L-BFGS等开发接口。

算子组合机制

组合机制为飞桨最新创新技术之一，旨在降低飞桨手写算子数量，低成本实现高阶微分、硬件接入、编译器接入。该技术核心是定义少量基础算子集合，即加减乘除等基础处理运算，针对该少量算子集实现反向微分等规则，然后将复杂算子拆解为基础算子组合表示。预期最终态飞桨前向算子数量由600+降低到300左右，且大部分场景不再需要手写高阶算子，实现高阶微分、新硬件接入、编译器接入成本的大幅降低。

编译优化

编译器是上述技术路线中加速模型训推速度的关键技术。其主要技术点在于将基础算子IR表示映射到编译器高层IR表示，并通过高级别的PASS优化进行整图优化操作，如算子融合、常量折叠、代数化简、无关计算剪枝与变量释放等。然后将高层IR转成硬件无关的低层IR表示，自动生成适配不同硬件的代码。通过使用神经网络编译器技术，Laplace方程求解性能提升3倍。

硬件支持

当前飞桨针对科学计算算子，在国产硬件DCU和XPU上加速适配，其中DCU上已经能够全量运行以飞桨为后端的DeepXDE。

科学计算工具组件赛桨 PaddleScience v1.0

基于飞桨深度学习框架的高层API以及高阶自动微分机制，飞桨同步升级并推出了科学计算工具组件赛桨PaddleScience v1.0。针对传统数值计算方法面临的维数高、耗时长、跨尺度的挑战，综合数学计算与物理数据相结合的处理方法，提供物理机理、数据驱动等范式来求解问题。同时围绕计算流体力学（CFD）、结构有限元仿真、气象预测等领域构建经典的AI for Science领域案例，为广大科研工作者提供可复用的案例开源代码以促进AI与基础科学的融合。

赛桨PaddleScience v1.0正式版包含了如下四方面的特色：

API架构更新

从用户使用习惯角度，兼顾深度学习及CFD&CAE用户体验，从数据预处理、模型选择、网络优化求解、结果后处理等角度更新API元素，提升用户使用感受。

丰富的场景案例

提供2D & 3D圆柱绕流、涡激振动、对流散热及方程反演等基础案例，同时新增结构领域中2D & 3D结构受力分析案例，气象领域中气象预报、污染物扩散等相关案例，支持直接复用及二次开发，用户可从Github代码仓直接体验相关项目的AIStudio实践。

底层模型更新

新增如CNN、U-Net、Transformer、GAN等经典神经网络模型以及FNO算子学习模型，并提供相应验证案例。

API升级更新

提供全新设计的API供用户自定义偏微分方程及定义各类边界条件，支持2D & 3D基础几何定义、STL复杂外形解析及布尔操作等，并提供准随机采样、局部加密采样等功能。

具体功能可详见

https://paddlescience-docs-hss.readthedocs.io/zh/latest/

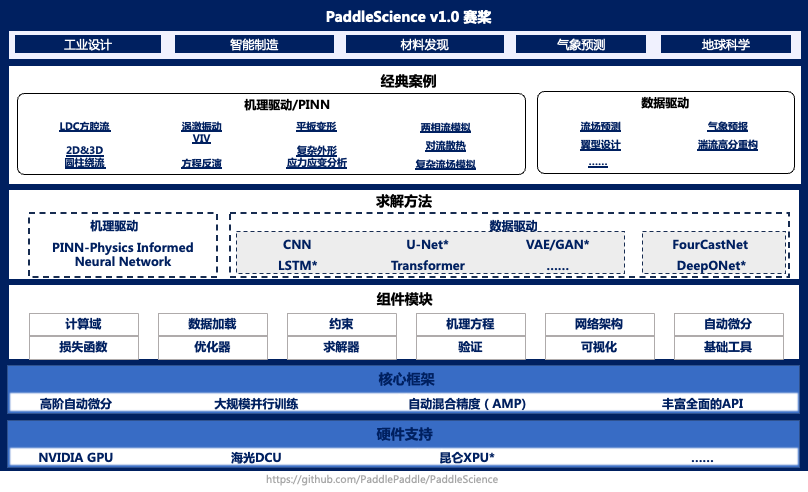
图 PaddleScience v1.0产品全景（ 建设中）*

赛桨提供应用于科学计算问题的端到端API，结合常见CFD业务流程中涉及的前处理、求解、后处理等过程，提供计算域定义、深度学习求解、推理及可视化等模块，并细分为Equation 、Geometry 、Constraint、Arch等API，工具组件设计架构如下。

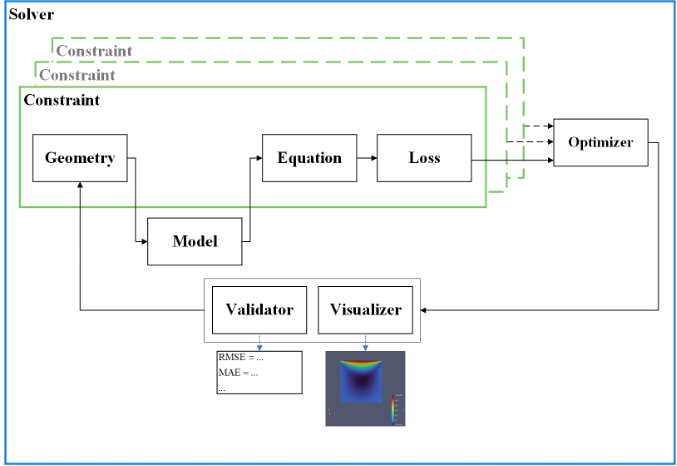
图 PaddleScience科学计算工具组件设计架构

方程（Equation）

赛桨支持调用预置方程接口及自定义方程接口，支持任意阶次的常微分（ODE)、偏微分(PDE)等方程定义，同时预置了如Navier-Stokes方程、Laplace方程等接口，可直接修改、使用。

计算域（Geometry）

赛桨提供常用的2D & 3D 规则几何，包括线段、圆、多边形、长方体、球体等。同时支持外部CAD工具生成*.STL格式文件的导入、解析及局部加密采样等功能，并提供几何体之间的布尔运算，以支撑任意复杂计算域的定义。

约束（Constraint）

赛桨最新的Constraint约束模块，提供了任意数据源的计算约束定义。包含计算过程中的物理边界条件（Boundary Conditions）约束以及目标信息监督约束，支持基础的三类边界条件（Dirichlet/Neumann/Robin BC）及用户自定义边界条件(General BC)定义，可支撑物理机理（数据主要来自几何）、数据驱动（数据主要来自数据文件）、数理融合（数据来自几何和数据文件）三种不同的训练范式。

网络（Arch）

赛桨支持多种网络模型结构，包括多层感知机（MLP）、Transformer等。提供网络参数初始化定义及预训练网络参数加载等功能，并支持多种激活函数，包括Tanh、Silu、Relu等。

损失函数（Loss）

赛桨提供了多种预置的Loss计算方式，如MSELoss、MAELoss、L2RelativeLoss，同时支持多种粒度的Loss权重配置，如：

$Loss=Loss_{equation}+\omega _{ic}Loss_{ic}+\omega _{bc} {\textstyle \sum_{(i,j)}^{}} (out_{(i,j)} -label_{(i,j)} )\TeX$

优化器（Optimizer）

赛桨支持常见的一阶优化器SGD、Momentum、Adam、AdamW，同时支持二阶优化器L-BFGS进一步提升模型精度。

评估与与可视化（Validator、Visualizer）

赛桨采用训练、评估、可视化分离的代码设计方案。通过开启评估、可视化功能，以在训练时自动评估当前模型在指定数据集上的精度，并可视化结果。也可以直接载入预训练好的模型，手动评估、可视化。

高阶微分（AutoDiff）

赛桨基于飞桨框架的高阶微分能力，预置了一阶、二阶微分接口，并可进一步组合出三阶甚至更高阶的微分接口，以满足多种微分场景的需求。

飞桨AI for Science科学领域案例

针对流体、结构、传热以及气象等领域，飞桨框架完成了领域中广泛问题的网络模型验证，如可应用于稳态问题的CNN/U-Net网络，可应用于瞬态问题的LSTM/Transformer/GNN网络，以及应用于物理场重构问题的VAE/GAN网络等。同时，上述网络模型正持续集成到赛桨PaddleScience v1.0，与机理求解方法PINN一同，形成了PaddleScience的核心求解器。下面分别介绍PaddleScience在流体和结构两个领域的实践。

流体领域案例

在流体领域，结合赛桨 PaddleScience 从**「物理机理驱动」以及「数据驱动」**两个维度对流体问题进行了分析与求解。

其中物理机理驱动主要应用PINN方法，将物理机理方程作为神经网络优化训练的控制函数。
数据驱动则利用经典神经网络或算子学习的方式构建代理模型。基于大量的训练数据，可以驱动经典神经网络模型，如Transformer、GNN、CNN等，同时也可以驱动算子学习，构建算子神经网络如FourCastNet、DeepONet等。

3D非定常圆柱绕流

赛桨PaddleScience v1.0目前可支持任意复杂外形的流场（如基于*STL外形文件的内、外流问题），并针对高雷诺流场问题，分析了Re=3900下，3D圆柱绕流的湍流特性。基于PINN方法以及半监督的训练方式（圆柱后端尾流区域采集了一定数量的监督点），实现对3D非定常不可压缩NS方程的求解。在结果分析阶段，分别从流场的速度、压力以及涡管结构等与LBM计算的结果进行对比，二者相对误差在5%以内。其中流场信息的对比结果如下图所示。

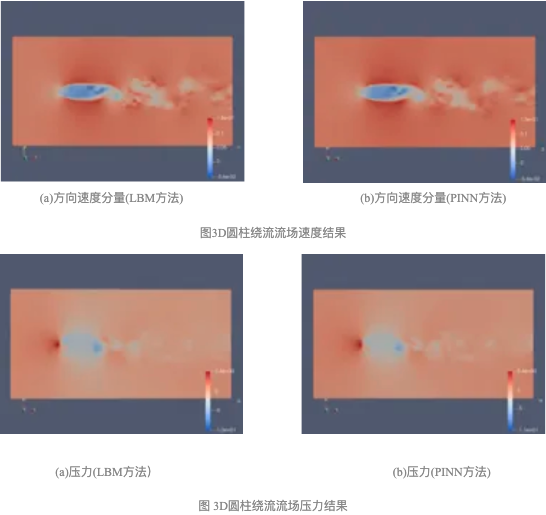
为了进一步分析流场结果的合理性，对神经网络模型的推理结果进行处理，得到涡管以及流线结果如下所示，结果从与LBM计算结果一致。

图 3D圆柱绕流流场涡管结构及流线图

基于TransformerPHX的流场预测

Transformer网络通过注意力机制计算模型输入与输出的隐含表示，目前已经广泛应用于NLP、CV等领域。在科学计算中，通过将物理信息（数据、图片等）映射为词向量，也可采用Transformer架构实现物理问题的拟合与结果预测，如在数据驱动的气象预报中，Transformer已经展现出了令人瞩目的效果。
本案例为基于赛桨对论文Transformer-PHX中网络模型及相关案例进行的复现。围绕文中2D非定常圆柱绕流、Lorenz方程等，重构了Transformer网络模型并在分别对文中提供的案例进行了验证，网络结构如下图所示。

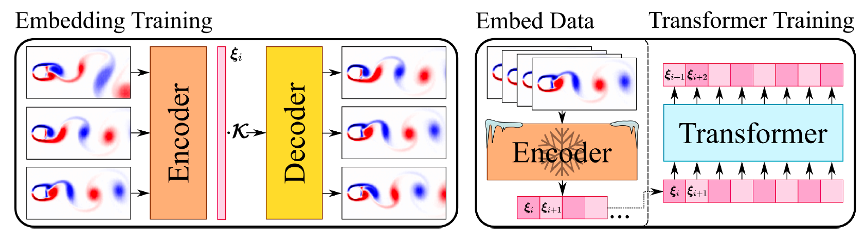
图 Transformer-PHX网络结构图（图片来源于[Geneva et al.,2020]）

案例中所用的训练数据集基于OpenFoam生成的分辨率为64128，时间步长为0.5s，并在雷诺数100 ~ 750的范围内随机选取仿真结果。完成模型训练后可对100 ~ 750雷诺数范围内的任意工况下实现流场结构的推理。在Re=100工况下，基于Transformer模型推理与OpenFoam计算得到的流场中速度ux、速度uy、压力的对比结果下图所示，其中OpenFoam结果的前缀为“target_”，Transformer模型的预测结果的前缀为“pred_”，图中展示了180个时间步的预测结果。

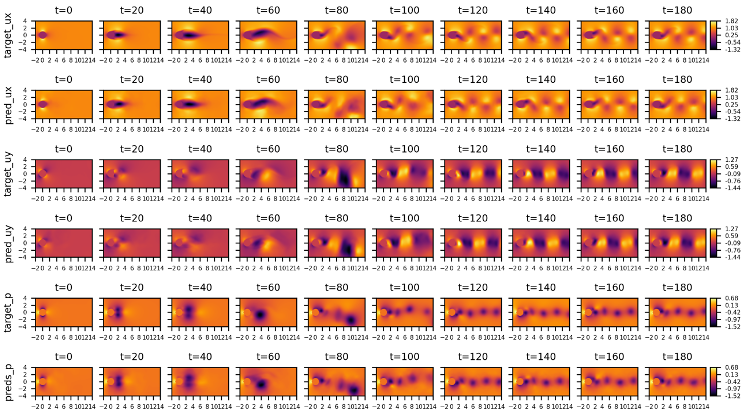
图 TransformerPHX结果与OpenFoam结果对比

案例链接

https://github.com/PaddlePaddle/PaddleScience/tree/release/1.0/examples/cylinder/2d_unsteady/transformer_physx

结构领域案例

在结构领域中，飞机机翼桁架、汽车底盘、轮船甲板等机械结构件的受力变形、破坏以及疲劳损伤等都是最典型的“力学”工程难题，这类结构问题通常可由平衡微分方程、几何方程和物理方程来描述。传统的结构分析方法包括有限元法、有限差分法、边界元法等，往往需要大量的计算资源和人力投入，这会限制模型的规模和精度。基于物理信息神经网络（PINN）的AI方法被证明可有效地求解结构领域的物理方程，兼具提升计算速度与减低人力投入的优势。

3D复杂结构变形分析

实际场景中的结构多为复杂的拓扑外形，一般基于专业CAD工具绘制，如Catia/Cero/SolidWorks等，且在进行结构应力应变分析时，用户通常需要对结构进行适当的网格划分，进而借助专业的有限元仿真工具进行受力分析，如Abaqus/ANSYS等。赛桨针对复杂结构外形设计了全新的几何API，支持解析常见CAD工具导出的 *.STL中间格式，支持对 *.STL文件进行布尔操作及局部加密采样。此外，针对各向同性材料的线弹性方程，也进行了详细定义与验证。

平衡方程： $\bigtriangledown·\sigma + f = \rho \frac{\partial ^{2 }{u} }{\partial ^{2 }{t} }$

协调方程： $\begin{bmatrix} \sigma _{xx} \\ \sigma _{yy} \\ \sigma _{zz} \\ \sigma _{xy} \\ \sigma _{yz} \\ \sigma _{zx} \\ \end{bmatrix} = \begin{bmatrix} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \varepsilon _{zz} \\ \varepsilon _{xy} \\ \varepsilon _{yz} \\ \varepsilon _{zx} \\ \end{bmatrix}$

本构方程： $\begin{bmatrix} \sigma _{xx} \\ \sigma _{yy} \\ \sigma _{zz} \\ \sigma _{xy} \\ \sigma _{yz} \\ \sigma _{zx} \\ \end{bmatrix} = \begin{bmatrix} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \varepsilon _{zz} \\ \varepsilon _{xy} \\ \varepsilon _{yz} \\ \varepsilon _{zx} \\ \end{bmatrix}$

基于上述方程可对线弹性材料进行在小应变条件下的线性弹性行为分析，参照Modulus工具提供的线弹性结构变形案例Bracket，结构左端表面固定，右端表面施加 -Y方向的均布载荷，计算静平衡状态下整个结构的受力与变形。赛桨实现了在PINN方法下无监督的求解结构变形，且得到的结果与Modulus一致。结果如下，分别为结构在X, Y, Z方向的变形以及三个方向的主应力。由于受到-Y方向的均布载荷，所以结构的右端（X方向）沿着-Z方向变形位移最大。同样在结构左侧连接位置受到的载荷（）最大。（详细代码之后会同步在AIStduio 科学计算项目集中）。

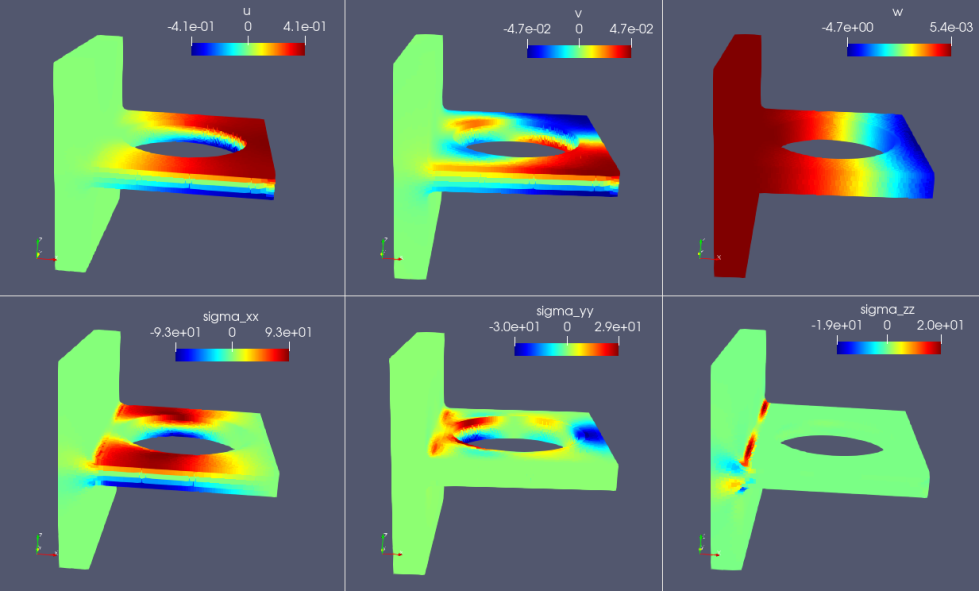
图 PINN方法求解结果（上：x,y,z方向结构变形位移结果；下：结构主应力结果）

总结

近几年，百度飞桨持续全力投入AI for Science的产品创新和交叉型科研生态建设。在产品层面，飞桨框架持续提升对泛科研场景的支撑能力，同时从复杂科研场景的快速实现、科研领域用户使用习惯无差别迁移等方面不断迭代科学计算工具组件赛桨PaddleScience。我们本次为大家带来飞桨最新的框架机制以及开源的赛桨PaddleScience v1.0正式版，希望能够进一步推动AI for Science基础软件的开源活跃度，促进多学科交叉复合型人才建设及加快完善基础软件技术生态体系建设。

拓展阅读