并查集

https://oi-wiki.org/ds/dsu/
在这里插入图片描述

操作：

将两个集合合并
询问两个元素是否在一个集合当中

（路径压缩优化之后）：近乎 $O (1)$

算法原理（重要！⭐）

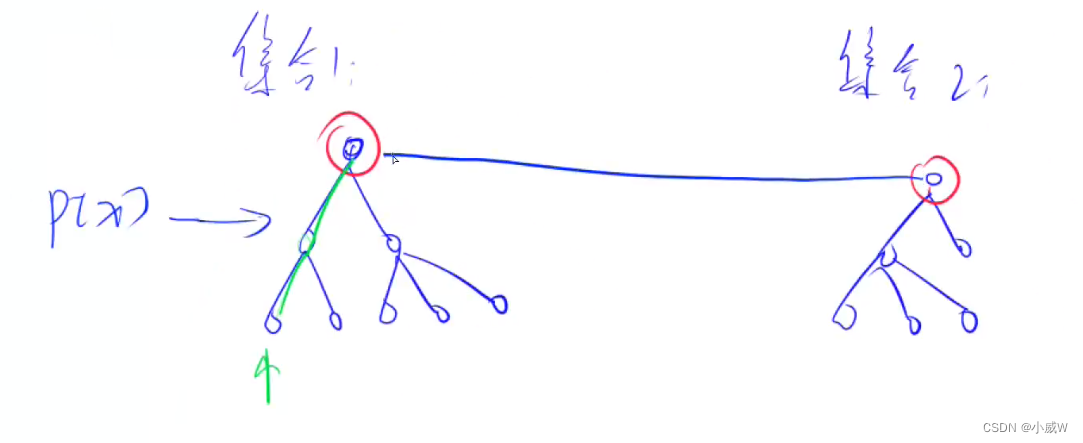
在这里插入图片描述

将每个集合使用树的形式存储。

每个集合的编号是树根的编号。

每个节点存储它的父节点是谁。 p[x] 表示 x 的父节点。

Q：如何判断树根？
A：p[x] == x

Q：如何求 x 的集合编号？
A：while (p[x] != x) x = p[x];
使用 路径压缩 的话就是 if (p[x] != x) p[x] = find(x);

Q：如何合并两个集合？
A：p[x] = y，即把一棵树的根节点当成另一个树根节点的儿子。（优化！：将这棵树中的所有节点都当成另一棵树根节点的子节点——优化之后几乎就是 $O (1)$ 的了）（这个优化叫做 路径压缩）

经典例题

836. 合并集合（重要！模板！⭐）

https://www.acwing.com/activity/content/problem/content/885/
在这里插入图片描述

注意下面 find(x) 的写法。

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int[] p;
    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(), m = scanner.nextInt();
        p = new int[n + 1];
        Arrays.setAll(p, e -> e);   // 初始化，各个节点的祖宗节点设置成自己
        while (m-- != 0) {
            char op = scanner.next().charAt(0);
            int a = scanner.nextInt(), b = scanner.nextInt();
            if (op == 'M') {
                p[find(a)] = find(b);
            } else {
                if (find(a) == find(b)) System.out.println("Yes");
                else System.out.println("No");
            }
        }
    }

    // 返回 x 的祖宗节点 + 路径压缩
    static int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);	// 路径压缩
        return p[x];
    }
}

837. 连通块中点的数量（维护连通块大小的并查集）

https://www.acwing.com/activity/content/problem/content/886/

在这里插入图片描述

find(x) 方法没有变化。

在合并两个点时：
先检查两个点是否已经在同一个连通块里了，直接 continue；
否则，先将一个点的根节点维护的数量加到另一个点的根节点维护的数量，然后再合并这两个点。

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int[] p, size;       // p[i][0]是父节点  p[i][1]是该连通块中点的数量
    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(), m = scanner.nextInt();
        p = new int[n + 1];
        size = new int[n + 1];
        Arrays.setAll(p, e ->e);   // 初始化，各个节点的祖宗节点设置成自己
        Arrays.fill(size, 1);   // 初始化每个连通块的大小是 1
        while (m-- != 0) {
            String op = scanner.next();
            int a = scanner.nextInt();
            if ("C".equals(op)) {
                int b = scanner.nextInt();
                if (find(a) == find(b)) continue;       // 已经在同一个连通块里了
                size[find(b)] += size[find(a)];
                p[find(a)] = find(b);
            } else if ("Q1".equals(op)) {
                int b = scanner.nextInt();
                if (find(a) == find(b)) System.out.println("Yes");
                else System.out.println("No");
            } else {
                System.out.println(size[find(a)]);
            }
        }
    }

    // 返回 x 的祖宗节点 + 路径压缩
    static int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
}

240. 食物链（维护额外信息的并查集）🚹🚹🚹

https://www.acwing.com/activity/content/problem/content/887/
在这里插入图片描述

同一个集合表示：这一个集合内的所有动物之间的关系都可以确定。

对于每一句话中的 x 和 y，先检查它们是否在一个集合里，如果在同一个集合里，那么就可以判断这句话是否是假话。
如果是假话—— ++ans
如果是真话—— 将它们所在的两个集合合并。

如何确定同一个集合里各个动物之间的关系？
使用 d 数组维护各个节点到根节点之间的距离。（具体可以看下图：）

在这里插入图片描述
注意看代码中注释的解释。

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int[] p, d;
    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(), k = scanner.nextInt(), ans = 0;
        // 一个集合里的所有动物之间的关系是可以推理出来的（这里同一个连通块并不表示它们是同一个种类，而是它们之间的关系可以确定）
        // 记录每个点和根节点的关系（用每个点和根节点之间的距离来表示它和根节点之间的距离）
        p = new int[n + 1];
        Arrays.setAll(p, e ->e);    // 初始化，各个节点的祖宗节点设置成自己
        d = new int[n + 1];         // d 维护的是各个节点到根节点的距离（距离表示它和根节点之间的关系）

        while (k-- != 0) {
            int op = scanner.nextInt(), x = scanner.nextInt(), y = scanner.nextInt();
            if (x > n || y > n) {               // x 或 y 比 n 大 —— 是假话
                ++ans;
                continue;
            }

            int px = find(x), py = find(y);     // 找到 x 和 y 的祖宗节点
            if (op == 1) {
                if (px == py && (d[x] - d[y]) % 3 != 0) ++ans;  // 已经在一个集合里了，判断是否合理
                else if (px != py) {            // 不在一个集合里，确定关系
                    p[px] = p[py];
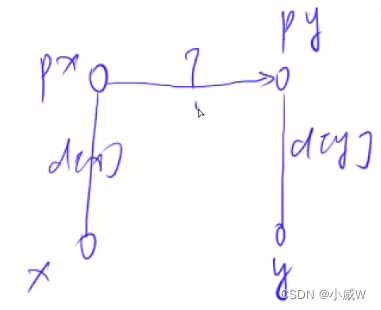
                    d[px] = d[y] - d[x];        // 是为了令 d[px] + d[x] == d[y]
                }
            } else {
                if (px == py && (d[x] - d[y] - 1) % 3 != 0) ans++;  // 已经在一个集合里了，判断是否合理
                else if (px != py) {
                    p[px] = py;
                    d[px] = d[y] - d[x] + 1;    // x 吃 y，是为了令d[px] + d[x] = d[y] + 1。
                }
            }
        }
        System.out.println(ans);
    }

    static int find(int x) {
        if (p[x] != x) {
            int t = find(p[x]);     // t 是 x 的父节点的父节点
            d[x] += d[p[x]];        // 在路径压缩的过程中，子节点需要继承父节点到根节点的距离。（因为没压缩之前 d[x]是x到p[x]之间的距离）
            p[x] = t;
        }
        return p[x];
    }
}