《数据结构》数据结构概念,顺序表,链表

news2024/11/25 20:22:26

目录

1. 为什么学习数据结构？

2. 数据结构

2.1. 数据

2.2. 逻辑结构

2.3. 存储结构

2.4. 操作

3. 算法

3.1. 算法与程序

3.2. 算法与数据结构

3.3. 算法的特性

3.4. 如何评价一个算法的好坏

4. 线性表

4.1. 顺序表

4.2. 单向链表

4.3. 单向循环链表（解决约瑟夫问题）

1. 为什么学习数据结构？

C语言：学习的时如何写代码

数据结构：教会我们高效简洁的写代码。

实现一个功能、写代码解决什么问题？

1》数据与数据之间的逻辑规律和数据在计算机中如何表示(存储)

数据结构：数据的逻辑结构存储结构及操作

数据：不只是一个单独的数值、是一个集合的概念。

2》解决问题的方法(实现代码的逻辑思想)

算法

数据结构+算法=程序

2. 数据结构

概念： 数据的逻辑结构存储结构及操作。

2.1. 数据

数据：不只是一个单独的数值，是一个集合的概念。

数据元素：数据的最小单位，由基本的数据项构成。

数据项：是数据元素的基本单位，描述数据元素拥有的信息。

节点：就是数据元素

2.2. 逻辑结构

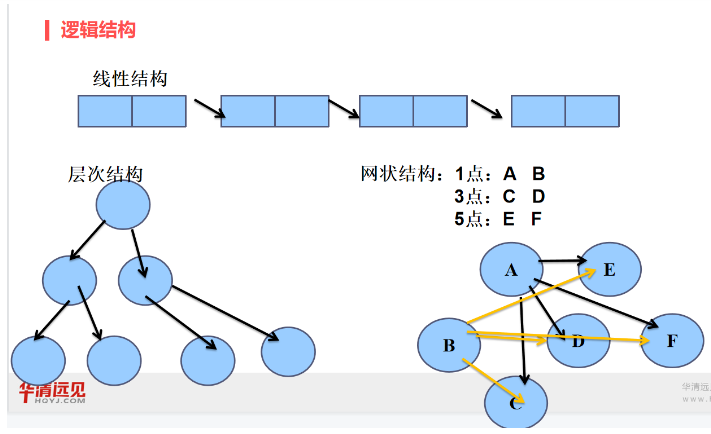
概念：描述数据之间的逻辑规律和联系，即元素与元素之间的关系

逻辑结构的分类：

  1. 线性结构（头节点无前驱，尾节点无后缀）
    1. 线性存储
    2. 一对一的关系
    3. 顺序表、链表
  1. 层次结构（根节点无前驱，叶子节点无后继）
    1. 一对多的关系
  1. 网状结构
    1. 多对多的关系
    2. 图

2.3. 存储结构

概念：数据的逻辑结构在计算机中的具体实现

  1. 存储结构分类
    1. 顺序存储：内存空间开辟是连续（数组：内存空间连续开辟，数据元素类型相同）
    2. 链式存储：通过地址将数据元素联系在一起
    3. 索引存储：通过索引表找到数据元素存放位置，拿到数据
    4. 散列存储结构 (哈希存储)
      1. 数据元素的存放和位置之间存在一个关系。
      2. 存在一个关键字key和一个关系函数，通过关键值key带入关系函数计算出数据存放的位置。对应位置存放、对应位置取值。

2.4. 操作

操作：增 删 改 查

3. 算法

3.1. 算法与程序

算法：解决问题的思想办法

程序：用计算机语言对算法的具体实现

3.2. 算法与数据结构

算法+数据结构=程序

算法的设计：依赖于逻辑结构

算法的实现：依赖于存储结构

3.3. 算法的特性

  1. 有穷性：算法的执行步骤是有限的
  2. 确定性：算法的每一个步骤，无二义性 ，没有歧义
  3. 可行性：算法能够在有限的时间内完成
  4. 输入和输出：一个算法可以有一个或多个输入和输出

3.4. 如何评价一个算法的好坏

  1. 正确性：保证算法能够正确的完成功能的实现
  2. 易读性：算法容易被解读
  3. 健壮性：错误处理
  4. 高效性：算法执行效率，算法执行快慢容易受到计算机性能的
  5. 低存储性：算法占用空间小，空间复杂度

4. 线性表

  • 线性表：
    • 顺序表
    • 链表(单向链表 单向循环链表 双向链表 双向循环链表)
    • 栈
    • 队列
  • 特点：一对一的关系，头节点没有前驱，尾节点没有后继

4.1. 顺序表

  • 特点：内存空间是连续开辟(数组)
  • 逻辑结构：线性结构
  • 存储结构：顺序存储结构
  • 定义一个结构体表示顺序表
#define  N 10
typedef  int   datatype_t;
typedef struct  list_t
 {
	datatype_t  data[N];//表
	int last ;			//保存最后一个有效元素的下标 (-1 表为空)
 }seqlist_t,*seqlist_pj;
 

  • 常见操作
 

#include <stdio.h>
#include <stdlib.h>

#define N 10

typedef int datatype_t;

typedef struct list_t {
    datatype_t data[N]; 	// 表
    int last; 				// 保存最后一个有效元素的下标 (-1 表为空)
} seqlist_t, *seqlist_p;

// 创建一个空的顺序表
seqlist_p createList() {
    seqlist_p list = (seqlist_p)malloc(sizeof(seqlist_t));
    list->last = -1;
    return list;
}

// 向顺序表的指定位置插入数据
void insert(seqlist_p list, int pos, int value) {
    if (pos < 0 || pos > list->last + 1 || list->last == N - 1) {
        printf("插入位置无效或顺序表已满\n");
        return;
    }
    
    // 将插入位置之后的元素依次后移
    for (int i = list->last; i >= pos; i--) {
        list->data[i+1] = list->data[i];
    }
    
    // 在指定位置插入新元素
    list->data[pos] = value;
    list->last++;
}

// 判断顺序表是否满
int isFull(seqlist_p list) {
    return list->last == N - 1;
}

// 指定位置删除数据
void delete(seqlist_p list, int pos) {
    if (pos < 0 || pos > list->last) {
        printf("删除位置无效\n");
        return;
    }
    
    // 将删除位置之后的元素依次前移
    for (int i = pos; i < list->last; i++) {
        list->data[i] = list->data[i+1];
    }
    
    list->last--;
}

// 判断顺序表是否为空
int isEmpty(seqlist_p list) {
    return list->last == -1;
}

// 修改指定位置的数据
void modify(seqlist_p list, int pos, int value) {
    if (pos < 0 || pos > list->last) {
        printf("修改位置无效\n");
        return;
    }
    
    list->data[pos] = value;
}

// 删除指定的数据
void removeData(seqlist_p list, int value) {
    for (int i = 0; i <= list->last; i++) {
        if (list->data[i] == value) {
            // 将删除位置之后的元素依次前移
            for (int j = i; j < list->last; j++) {
                list->data[j] = list->data[j+1];
            }
            list->last--;
            i--; // i减1以继续判断下一个元素是否与value相等
        }
    }
}

// 清空顺序表
void clearList(seqlist_p list) {
    list->last = -1;
}

// 删除顺序表
void deleteList(seqlist_p list) {
    free(list);
}

// 遍历顺序表
void traverse(seqlist_p list) {
    if (isEmpty(list)) {
        printf("顺序表为空\n");
        return;
    }
    
    printf("顺序表数据：");
    for (int i = 0; i <= list->last; i++) {
        printf("%d ", list->data[i]);
    }
    printf("\n");
}

int main() {
    seqlist_p list = createList();
    insert(list, 0, 1);
    insert(list, 1, 2);
    insert(list, 2, 3);
    traverse(list);
    delete(list, 1);
    traverse(list);
    modify(list, 0, 5);
    traverse(list);
    removeData(list, 5);
    traverse(list);
    clearList(list);
    traverse(list);
    deleteList(list);
    return 0;
}
 

 

  • 顺序表的特点
 

1.内存空间连续开辟
 

2.长度固定(保存的数据元素个数是固定的) #define N 10
 

3.插入和删除比较复杂，查询操作或修改比较简单。
 

4.2. 单向链表
 

  • 特点：内存空间开辟不是连续、通过地址将多有的内存空间练习到一起
  • 逻辑结构：线性结构
  • 存储结构：链式存储
  • 分类：
 

  •  
  
    • 有头单向链表
 

  •  
  
    •  
    
      • 链表中的头节点数据域无效，指针域有效
 

  •  
  
    • 无头单向链表
 

  •  
  
    •  
    
      • 链表中所有节点的数据域和指针域都是有效的
 

  • 定义链表节点结构体：
 

typedef  int  datatype_t;
typedef struct  node_t 		//node 节点
{
	datatype_t data;		//数据域
	struct node_t *next;	//指针域		保存下一个节点的地址
}linklist_t,*linklist_p;	//link		链
 

 

  • 有头单向链表
 

#include <stdio.h>
#include <stdlib.h>

typedef int datatype_t;
typedef struct node_t
{
    datatype_t data;		//数据域
    struct node_t *next;	//节点域
}linklist_t, *linklist_p;

// 创建空的有头单向链表
void createEmptyList(linklist_p *head)
{
    *head = (linklist_p)malloc(sizeof(linklist_t));
    (*head)->next = NULL;
}

// 向链表的指定位置插入数据
void insertData(linklist_p head, int position, datatype_t data)
{
    linklist_p p = head;
    int count = 0;

    while (p && count < position)
    {
        p = p->next;
        count++;
    }

    if (p && count == position)
    {
        linklist_p newNode = (linklist_p)malloc(sizeof(linklist_t));
        newNode->data = data;
        newNode->next = p->next;
        p->next = newNode;
    }
}

// 计算链表的长度
int calculateLength(linklist_p head)
{
    linklist_p p = head->next;
    int length = 0;

    while (p)
    {
        length++;
        p = p->next;
    }

    return length;
}

// 遍历链表
void traverseList(linklist_p head)
{
    linklist_p p = head->next;

    while (p)
    {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

// 删除链表指定位置的节点
void deleteNode(linklist_p head, int position)
{
    linklist_p p = head;
    int count = 0;

    while (p && count < position)
    {
        p = p->next;
        count++;
    }

    if (p && p->next && count == position)
    {
        linklist_p temp = p->next;
        p->next = p->next->next;
        free(temp);
    }
}

// 修改链表指定位置的数据
void modifyData(linklist_p head, int position, datatype_t data)
{
    linklist_p p = head->next;
    int count = 0;

    while (p && count < position)
    {
        p = p->next;
        count++;
    }

    if (p && count == position)
    {
        p->data = data;
    }
}

// 查询指定数据的位置
int findPosition(linklist_p head, datatype_t data)
{
    linklist_p p = head->next;
    int position = 0;

    while (p)
    {
        if (p->data == data)
        {
            return position;
        }
        p = p->next;
        position++;
    }

    return -1;
}

// 删除指定的数据
void deleteData(linklist_p head, datatype_t data)
{
    linklist_p p = head;

    while (p->next)
    {
        if (p->next->data == data)
        {
            linklist_p temp = p->next;
            p->next = p->next->next;
            free(temp);
        }
        else
        {
            p = p->next;
        }
    }
}

// 清空链表
void clearList(linklist_p head)
{
    linklist_p p = head->next;

    while (p)
    {
        linklist_p temp = p;
        p = p->next;
        free(temp);
    }

    head->next = NULL;
}

// 链表的倒置
void reverseList(linklist_p *head)
{
    linklist_p prev = NULL;
    linklist_p current = *head;
    linklist_p next = NULL;

    while (current != NULL)
    {
        next = current->next;
        current->next = prev;
        prev = current;
        current = next;
    }

    *head = prev;
}

// 判断链表是否为空
int isEmpty(linklist_p head)
{
    return head->next == NULL;
}

int main()
{
    linklist_p head;
    createEmptyList(&head);

    insertData(head, 0, 1);
    insertData(head, 1, 2);
    insertData(head, 2, 3);
    insertData(head, 3, 4);
    insertData(head, 4, 5);

    printf("List: ");
    traverseList(head);

    printf("Length: %d\n", calculateLength(head));

    deleteNode(head, 2);
    printf("After deleting node at position 2: ");
    traverseList(head);

    modifyData(head, 1, 10);
    printf("After modifying data at position 1: ");
    traverseList(head);

    int position = findPosition(head, 5);
    printf("Position of data 5: %d\n", position);

    deleteData(head, 1);
    printf("After deleting data 1: ");
    traverseList(head);

    clearList(head);
    printf("After clearing the list: ");
    traverseList(head);

    insertData(head, 0, 1);
    insertData(head, 1, 2);
    insertData(head, 2, 3);
    insertData(head, 3, 4);
    insertData(head, 4, 5);

    printf("List: ");
    traverseList(head);

    reverseList(&head);
    printf("After reversing the list: ");
    traverseList(head);

    printf("Is list empty? %s\n", isEmpty(head) ? "Yes" : "No");

    return 0;
}
 

 

  • 无头单向链表
 

#include <stdio.h>
#include <stdlib.h>

// typedef定义的数据类型
typedef int datatype_t;
typedef struct node_t {
    datatype_t data;
    struct node_t* next;
} linklist_t, * linklist_p;

// 创建空的有头单向链表
void createEmptyList(linklist_p* head) {
    *head = NULL;
}

// 向链表的指定位置插入数据
int insertElement(linklist_p* head, int position, datatype_t value) {
    // 创建新节点
    linklist_p new_node = (linklist_p)malloc(sizeof(linklist_t));
    if (new_node == NULL) {
        return 0;  // 内存分配失败
    }
    new_node->data = value;
    new_node->next = NULL;

    if (position == 0) {
        new_node->next = *head;
        *head = new_node;
    }
    else {
        int count = 0;
        linklist_p current = *head;
        while (current != NULL && count < position - 1) {
            current = current->next;
            count++;
        }

        if (current == NULL) {
            return 0;  // 指定位置无效
        }

        new_node->next = current->next;
        current->next = new_node;
    }

    return 1;
}

// 计算链表的长度
int getLength(linklist_p head) {
    int length = 0;
    linklist_p current = head;
    while (current != NULL) {
        length++;
        current = current->next;
    }
    return length;
}

// 遍历链表
void traverse(linklist_p head) {
    linklist_p current = head;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

// 删除链表指定位置的数据
int deleteElement(linklist_p* head, int position) {
    if (*head == NULL) {
        return 0;  // 链表为空
    }

    if (position == 0) {
        linklist_p temp = *head;
        *head = (*head)->next;
        free(temp);
    }
    else {
        int count = 0;
        linklist_p current = *head;
        linklist_p previous = NULL;
        while (current != NULL && count < position) {
            previous = current;
            current = current->next;
            count++;
        }

        if (current == NULL) {
            return 0;  // 指定位置无效
        }

        previous->next = current->next;
        free(current);
    }

    return 1;
}

// 修改链表指定位置的数据
int modifyElement(linklist_p head, int position, datatype_t value) {
    int count = 0;
    linklist_p current = head;
    while (current != NULL && count < position) {
        current = current->next;
        count++;
    }

    if (current == NULL) {
        return 0;  // 指定位置无效
    }

    current->data = value;

    return 1;
}

// 查询指定数据的位置
int findPosition(linklist_p head, datatype_t value) {
    int position = 0;
    linklist_p current = head;
    while (current != NULL) {
        if (current->data == value) {
            return position;
        }
        current = current->next;
        position++;
    }
    return -1;  // 没有找到指定数据
}

// 删除指定的数据
int deleteValue(linklist_p* head, datatype_t value) {
    if (*head == NULL) {
        return 0;  // 链表为空
    }

    if ((*head)->data == value) {
        linklist_p temp = *head;
        *head = (*head)->next;
        free(temp);
        return 1;
    }

    linklist_p current = *head;
    linklist_p previous = NULL;
    while (current != NULL && current->data != value) {
        previous = current;
        current = current->next;
    }

    if (current == NULL) {
        return 0;  // 没有找到指定数据
    }

    previous->next = current->next;
    free(current);
    return 1;
}

// 清空链表
void clearList(linklist_p* head) {
    linklist_p current = *head;
    while (current != NULL) {
        linklist_p temp = current;
        current = current->next;
        free(temp);
    }
    *head = NULL;
}

// 链表的倒置
void reverseList(linklist_p* head) {
    linklist_p previous = NULL;
    linklist_p current = *head;
    linklist_p next = NULL;

    while (current != NULL) {
        next = current->next;
        current->next = previous;
        previous = current;
        current = next;
    }

    *head = previous;
}

// 判断链表是否为空
int isListEmpty(linklist_p head) {
    return head == NULL;
}

int main() {
    linklist_p linked_list;
    createEmptyList(&linked_list);

    insertElement(&linked_list, 0, 1);
    insertElement(&linked_list, 1, 2);
    insertElement(&linked_list, 2, 3);
    insertElement(&linked_list, 3, 4);

    traverse(linked_list);  // 输出: 1 2 3 4

    printf("Length: %d\n", getLength(linked_list));  // 输出: 4

    deleteElement(&linked_list, 2);

    traverse(linked_list);  // 输出: 1 2 4

    modifyElement(linked_list, 1, 5);

    traverse(linked_list);  // 输出: 1 5 4

    int position = findPosition(linked_list, 5);
    printf("Position: %d\n", position);  // 输出: 1

    deleteValue(&linked_list, 1);

    traverse(linked_list);  // 输出: 5 4

    clearList(&linked_list);

    printf("Is empty: %s\n", isListEmpty(linked_list) ? "Yes" : "No");  // 输出: Yes

    insertElement(&linked_list, 0, 1);
    insertElement(&linked_list, 1, 2);
    insertElement(&linked_list, 2, 3);
    insertElement(&linked_list, 3, 4);

    traverse(linked_list);  // 输出: 1 2 3 4

    reverseList(&linked_list);

    traverse(linked_list);  // 输出: 4 3 2 1

    return 0;
}
 

 

  • 链表的特点
 

1.内存空间不连续，通过地址将地址空间联系在一起
 

2.长度不固定
 

3.删除和插入简单，查询和修改复杂
 

4.3. 单向循环链表（解决约瑟夫问题）
 

  • 特点：无头单向链表尾节点的指针域保存头节点的地址， 就可以形成单向循环链表
  • 通过一定规律找到一个最终的值
  • 定义链表结构体
 

typedef struct node_t
{
    int data;
    struct node_t *next;
}link_t;
 

  • 单向循环链表
 

#include <stdio.h>
#include <stdlib.h>
#define N 10
typedef struct node_t
{
    int data;
    struct node_t *next;
} link_t;

int main()
{
    // 1.创建一个单向无头链表
    link_t *tail = NULL;
    link_t *p = (link_t *)malloc(sizeof(link_t));
    if (p == NULL)
    {
        puts("mallod error");
        return -1;
    }
    p->data = 1;
    p->next = NULL;
    tail = p; // 指针tail指向了p
    // 创建接下来的节点
    for (int i = 0; i < N; i++)
    {
        tail->next = (link_t *)malloc(sizeof(link_t));
        if (tail->next == NULL)
        {
            puts("mallod error");
            return -1;
        }
        tail = tail->next;
        tail->data = i + 1;
        tail->next = NULL;
    }
    tail->next = p; // 尾节点指向头节点
    // 解决约瑟夫问题
    int start_num = 3;
    int n = 3;
    link_t *pdel = NULL;
    // 1.将头指针移动到K
    for (int i = 0; i < start_num - 1; i++)
    {
        p = p->next;
    }
    pdel = p->next;
    while (p != p->next)
    {
        for (int i = 0; i < n - 1; i++)
            p = p->next;
        pdel = p->next;
        p->next = pdel->next;
        free(pdel);
        pdel = NULL;
    }
    printf("king is %d\n", p->data);
    return 0;
}
 

顺序表和单向链表比较
 

 
 		 
顺序表
 		 
链表
 
 
空间
 		 
空间连续
 		 
通过指针链接
 
 
长度
 		 
固定
 		 
不固定
 
 
特点
 		 
查找方便，但是插入和删除麻烦
 		 
插入方便，查找麻烦
 

                

        

        

            

            

            

              

                本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/770462.html
              

              如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！
            

            
            

              
            

          


            
相关文章

          
            
                  

                    

                      

                        

                          
                            使用NVIDIA FX Composer验证多纹理合成效果
                        

                      

                      

                        

                          使用NVIDIA FX Composer验证多纹理合成效果
                        

                        

                          最近项目上有一个需求&#xff0c;需要将4张带透明通道纹理合成为一张&#xff0c;并且每张纹理指定一个全局透明度。由于纹理过多&#xff0c;合成效果无法保证&#xff0c;为了减少项目的风险&#xff0c;领导希望我先快速验证一下我们讨论的方法是否能完成项目的要求。因此我…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            GO语言泛型
                        

                      

                      

                        

                          GO语言泛型
                        

                        

                          set一般没什么不方便的 但是使用GET 需要使用类型断言,将取出来的数据转为预期数据, 
空接口本身是一个装箱,会产生内存逃逸和多一部分空间. 于是1.17GO使用泛型. 泛型实现: 
分析可执行文件后:发现 也就是泛型会为每个数据类型都生产一套代码,导致可执行文件大小增加,并且使用…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            在企业使用jmeter开展实际的接口自动化测试工具
                        

                      

                      

                        

                          在企业使用jmeter开展实际的接口自动化测试工具
                        

                        

                          在企业使用jmeter开展实际的接口自动化测试工具&#xff0c;建议按如下操作流程&#xff0c; 可以使整个接口测试过程更规范&#xff0c;更有效。 
接口自动化的流程&#xff1a; 
1、获取到接口文档&#xff1a;swagger、word、excel ... 
2、熟悉接口文档然后设计测试用例&am…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            关于AES 和 BASE64 的理解
                        

                      

                      

                        

                          关于AES 和 BASE64 的理解
                        

                        

                          BASE64 
首先 base64 是一种编码方式&#xff0c;它的字符集由64个不同字符组成&#xff08;A-Z、a-z、0-9和两个额外字符/&#xff09;&#xff0c;因此每个Base64字符都占用6个比特&#xff08;2^6  64&#xff09; Base64编码后的数据长度  4 * ceil(原始数据长度 / 3) 其中…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            echarts 横向柱状图 刻度标签
                        

                      

                      

                        

                          echarts 横向柱状图 刻度标签
                        

                        

                          echarts 横向柱状图 刻度标签 怎么调试都不左对齐 将width去掉固定宽度 echarts会自适应
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            如何录音转文字：探寻声音的文字之舞
                        

                      

                      

                        

                          如何录音转文字：探寻声音的文字之舞
                        

                        

                          随着科技的飞速进步&#xff0c;人们对于信息的传递和记录变得越发便捷。在这个数字化时代&#xff0c;录音转文字技术无疑是一颗璀璨的明珠&#xff0c;它让声音和文字在交织中跳跃&#xff0c;为我们带来了新的感知和体验。在这篇文章中&#xff0c;我们将深入探讨录音转文字…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            DCDC芯片选型
                        

                      

                      

                        

                          DCDC芯片选型
                        

                        

                          一、BUCK芯片选型 最初MP2307特别好用&#xff0c;是由美国MPS公司推出
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            信息摘要 秘钥签名 数字签名 数字证书 数字验证 这都是什么东西？
                        

                      

                      

                        

                          信息摘要 秘钥签名 数字签名 数字证书 数字验证 这都是什么东西？
                        

                        

                          信息摘要 秘钥签名 数字签名 数字证书 数字验证 这都是什么东西&#xff1f; 
一下遇见这么多相近的名词&#xff0c;实在是难以区分理解&#xff0c;还是从这些概念产生的缘由理解吧 
先看需求&#xff1a;如何保证 数据 在网络中传输时正确的&#xff1f;有没有被篡改&#x…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            【算法 -- LeetCode】（022） 括号生成
                        

                      

                      

                        

                          【算法 -- LeetCode】（022） 括号生成
                        

                        

                          1、题目 
数字 n 代表生成括号的对数&#xff0c;请你设计一个函数&#xff0c;用于能够生成所有可能的并且 有效的 括号组合。 
示例 1&#xff1a; 输入&#xff1a;n  3 输出&#xff1a;[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”] 示例 2&#xff1a; 输入…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            软件测试测试用例
                        

                      

                      

                        

                          软件测试测试用例
                        

                        

                          等价类&#xff1a;把输入的数据可以分为有效的数据和无效的数据 
被测试的对象输入的数据&#xff1a; 
1、有效的数据 
2、无效的数据 
测试一个产品&#xff0c;需要考虑它的正确场景&#xff0c;也需要考虑它的异常场景 
边界值:边界值测试用例是针对等价类测试用例方法的补…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            7月第2周榜单丨飞瓜数据B站UP主排行榜（哔哩哔哩）发布！
                        

                      

                      

                        

                          7月第2周榜单丨飞瓜数据B站UP主排行榜（哔哩哔哩）发布！
                        

                        

                          飞瓜轻数发布2023年7月10日-7月16日飞瓜数据UP主排行榜&#xff08;B站平台&#xff09;&#xff0c;通过充电数、涨粉数、成长指数三个维度来体现UP主账号成长的情况&#xff0c;为用户提供B站号综合价值的数据参考&#xff0c;根据UP主成长情况用户能够快速找到运营能力强的B…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            【基于 GitLab 的 CI/CD 实践】04、GitLab Pipeline 实践（中）
                        

                      

                      

                        

                          【基于 GitLab 的 CI/CD 实践】04、GitLab Pipeline 实践（中）
                        

                        

                          目录 
cache 缓存 
cache:paths 
cache:key 缓存标记 
cache:key:files 文件变化自动创建缓存 
cache:key:prefix 组合生产 SHA 校验和 
cache:policy 缓存策略 
综合实例(一) 全局缓存 
Pipeline 日志分析  
Runner 缓存  
综合实例&#xff08;二&#xff09; 
artifacts 制品…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            NOTA P2 RM26，拮抗剂，与NOTA螯合剂偶联，结构式及相关应用介绍
                        

                      

                      

                        

                          NOTA P2 RM26，拮抗剂，与NOTA螯合剂偶联，结构式及相关应用介绍
                        

                        

                          资料编辑|陕西新研博美生物科技有限公司小编MISSwu​ 英文名称&#xff1a;NOTA-P2-RM26 
规格标准&#xff1a;1g、5g、10g CAS&#xff1a;N/A 分子式&#xff1a;C73H110N18O19 分子量&#xff1a;1543.8NOTA-P2-RM26结构式&#xff1a; 反应机理&#xff1a; NOTA-P2-RM26&…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            八股总结（七）MySQL与Redis
                        

                      

                      

                        

                          八股总结（七）MySQL与Redis
                        

                        

                          文章目录 MySQL基础概念数据库三大范式是什么&#xff1f; 索引 Redis基本概念1、为什么用Redis作为MySQL的缓存&#xff1f; 数据结构2、Redis包含哪些数据类型&#xff1f;使用场景是什么&#xff1f;3、五种场景的Redis数据类型底层都是怎么实现的&#xff1f; Redis线程网络…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            Mysql如何查询出两个日期之间的所有日期？
                        

                      

                      

                        

                          Mysql如何查询出两个日期之间的所有日期？
                        

                        

                          问题&#xff1a; 
有时我们在生成一些时间轴类似的数据时&#xff0c;要求数据库不管有没有指定天的数据&#xff0c;都要生成该时间节点&#xff0c;可用mysql.help_topic来解决此类问题&#xff0c;通过序列和日期函数相结合来满足我们的业务需求。 
例如&#xff1a;查询20…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            ASUS华硕ROG幻14 2021款GA401QM原厂Win10系统工厂模式带ASUS Recovery恢复功能
                        

                      

                      

                        

                          ASUS华硕ROG幻14 2021款GA401QM原厂Win10系统工厂模式带ASUS Recovery恢复功能
                        

                        

                          自带恢复分区、所有驱动、出厂主题壁纸LOGO、Office办公软件、奥创控制中心等预装程序 
所需要工具&#xff1a;16G或以上的U盘(非必需) 文件格式&#xff1a;HDI,SWP,OFS,EDN,KIT,TLK多个底包 文件大小&#xff1a;11.34GB 
注&#xff1a;恢复时会清空电脑上所有盘的数据&…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            Kotlin开发笔记:类型安全和转换
                        

                      

                      

                        

                          Kotlin开发笔记:类型安全和转换
                        

                        

                          Kotlin开发笔记:类型安全 类型安全是编程中非常重要的内容&#xff0c;在实际编程中我们总是会遇到许许多多的空指针异常&#xff0c;类型错误等异常。因此解决好类型安全的问题可以大大提升程序的健壮性。同时Kotlin针对类型安全就引入了许多有用的机制&#xff0c;它将帮助我…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            pytorch 2.0初探：和pytorch 1.13的速度对比
                        

                      

                      

                        

                          pytorch 2.0初探：和pytorch 1.13的速度对比
                        

                        

                          看到pytorch2.0出来了&#xff0c;而且宣传提速明显&#xff0c;一行代码即可提速43%左右&#xff1a; 
compiled_model  torch.compile(model) We then measure speedups and validate accuracy across these models. Since speedups can be dependent on data-type, we measu…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            Laf v1.0 发布：函数计算只有两种，30s 放弃的和 30s 上线的
                        

                      

                      

                        

                          Laf v1.0 发布：函数计算只有两种，30s 放弃的和 30s 上线的
                        

                        

                          一般情况下&#xff0c;开发一个系统都需要前端和后端&#xff0c;仅靠一个人几乎无法胜任&#xff0c;需要考虑的特性和功能非常多&#xff0c;比如&#xff1a; 
需要一个数据库来存放数据&#xff1b;需要一个文件存储来存放各种文件&#xff0c;比如图片文件&#xff1b;后…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            旅行社优惠卡app软件开发
                        

                      

                      

                        

                          旅行社优惠卡app软件开发
                        

                        

                          旅游行业的不断发展&#xff0c;越来越多的旅行社开始推出各种优惠卡来吸引游客。而随着智能手机的普及&#xff0c;开发一款旅行社优惠卡APP软件成为了一种必然的趋势。     该软件的主要功能是提供旅行社的各种优惠卡信息&#xff0c;包括优惠卡的种类、价格、使用范围、有效…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
       
      
        

        

          

            



                
                
                

            

          

          

            



              
推荐文章

              
            

          


          

            


                
                
                
            

          

          

            

              
最新文章

              
            

          

          

            

            
            
            
            

          

        

      

    

    

      

        

                    Copyright @ 2022~2023